- ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
- уравнение вида

где F- заданная действительная функция точки х=(xt, ..., х п )области Dевклидова пространства Е п,
 и действительных переменных
и действительных переменных
(и(х)- неизвестная функция) с неотрицательными целочисленными индексами i1 ,..., in,
 k=0, ..., т,
k=0, ..., т, по крайней мере одна из производных
по крайней мере одна из производных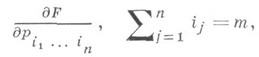
функции Fотлична от нуля; натуральное число тназ. порядком уравнения (1).
Определенная в области Dзадания уравнения (1) функция и(х), непрерывная вместе со своими частными производными, входящими в это уравнение и обращающая его в тождество, наз. регулярным решением. Наряду с регулярными решениями в теории Д. у. с ч. п. важное значение имеют решения, перестающие быть регулярными вблизи изолированных точек или многообразий особого вида: к ним относятся, в частности, элементарные (фундаментальные) решения. Они позволяют строить широкие классы регулярных решений (так наз. потенциалов) и устанавливать их структурные и качественные свойства.
В предположении непрерывности частных производных 1-го порядка функции Fотносительно переменных
 в теории уравнений вида (1) фундаментальную роль играет форма порядка т:
в теории уравнений вида (1) фундаментальную роль играет форма порядка т:
относительно действительных параметров l1, ...,l п, к-рая наз. характеристической формой, соответствующей уравнению (1).
Когда F- линейная функция переменных р i1, ... in, уравнение (1) наз. линейным. Линейное уравнение с частными производными 2-го порядка можно записать в виде:
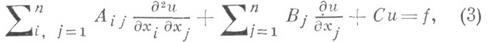
где Aij, Bj, С и f - заданные в области Dдействительные функции точки х. Уравнение (3) наз. однородным, если f(x)=0 для всех
 В случае уравнения (3) форма (2) является квадратичной:
В случае уравнения (3) форма (2) является квадратичной: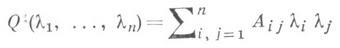
с коэффициентами Aij, зависящими только от точки
 В каждой точке
В каждой точке  квадратичная форма Qпри помощи неособого аффинного преобразования переменных li=li(x1, ..., xn), i=1, ..., п, может быть приведена к канонич. виду
квадратичная форма Qпри помощи неособого аффинного преобразования переменных li=li(x1, ..., xn), i=1, ..., п, может быть приведена к канонич. виду
где коэффициенты a, i=1, . . ., п, принимают значения 1, -1, 0, причем число отрицательных коэффициентов (индекс инерции) и число нулевых коэффициентов (дефект формы) являются аффинными инвариантами. Когда все ai= 1 или все ai =-1, т. е. когда форма Q соответственно положительно или отрицательно определена (дефинитна), уравнение (3) наз. эллиптическим в точке
 Если один из коэффициентов ai отрицателен, а все остальные положительны (или наоборот), то уравнение (3) наз. гиперболическим в точке х. В случае, когда l,l<l<n-1, коэффициентов ai положительны, а остальные п- Iотрицательны, уравнение (3) наз. ультрагиперболическим. Если же хотя бы один из этих коэффициентов (но не все) равен нулю, то уравнение (3) наз. параболическим в точке х. Говорят, что в области Dсвоего задания уравнение (3) является уравнением эллиптического, гиперболического или параболического типа, если оно соответственно эллиптично, гиперболично или параболично, в каждой точке этой области. Эллиптическое в области Dуравнение (3) наз. равномерно эллиптически м, если существуют действительные числа k0 и k1 одинакового знака такие, что
Если один из коэффициентов ai отрицателен, а все остальные положительны (или наоборот), то уравнение (3) наз. гиперболическим в точке х. В случае, когда l,l<l<n-1, коэффициентов ai положительны, а остальные п- Iотрицательны, уравнение (3) наз. ультрагиперболическим. Если же хотя бы один из этих коэффициентов (но не все) равен нулю, то уравнение (3) наз. параболическим в точке х. Говорят, что в области Dсвоего задания уравнение (3) является уравнением эллиптического, гиперболического или параболического типа, если оно соответственно эллиптично, гиперболично или параболично, в каждой точке этой области. Эллиптическое в области Dуравнение (3) наз. равномерно эллиптически м, если существуют действительные числа k0 и k1 одинакового знака такие, что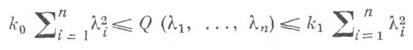
для всех
 Когда в разных частях области D
Когда в разных частях области Dуравнение (3) принадлежит к различным типам, то говорят, что оно является уравнением смешанного типа в этой области. Лапласа уравнение

теплопроводности уравнение

и волновое уравнение

являются типичными примерами линейных эллиптич., параболич. и гиперболич. уравнений 2-го порядка соответственно (подробнее см. Линейное гиперболическое уравнение и система, Линейное параболическое уравнение и система, Линейное эллиптическое уравнение и система).
Трикоми уравнение
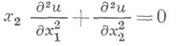
относится к уравнениям смешанного типа в любой области плоскости переменных х 1, х 2, пересечение к-рой с осью х 2 = 0 не пусто (подробнее см. Смешанного типа уравнение с частными производными).
В случае линейного уравнения с частными производными порядка т

где L1- линейный дифференциальный оператор с частными производными порядка ниже т, форма (2)имеет вид

Если при фиксированном значении
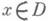 можно найти такое аффинное преобразование li=li(m1, ..., m п) i=1, ..., п, в результате к-рого полученная из (5) форма содержит лишь l,0<l<n, переменных m, то говорят, что уравнение (4) в точке хпараболически вырождается. При отсутствии параболич. вырождения и если конич. многообразие
можно найти такое аффинное преобразование li=li(m1, ..., m п) i=1, ..., п, в результате к-рого полученная из (5) форма содержит лишь l,0<l<n, переменных m, то говорят, что уравнение (4) в точке хпараболически вырождается. При отсутствии параболич. вырождения и если конич. многообразие
не имеет действительных точек, кроме l1=0, ..., ln=0 то уравнение (4) в точке хназ. эллиптическими Уравнение (4) наз. гиперболическим в точке х, если в пространстве переменных l1,..., l п существует прямая d такая, что если принять ее за координатную прямую в новых переменных m1, . . ., mn, полученных аффинным преобразованием l1, ..., ln, то относительно координаты, изменяющейся вдоль d, преобразованное уравнение (6) имеет ровно тдействительных корней (простых или кратных) при любом выборе остальных координат m.
Аналогичным образом по характеру формы (2) происходит классификация по типам уравнения (1) и в нелинейном случае. Поскольку в этом случае коэффициенты формы (2) зависят, наряду с точкой х, от искомого решения и от его производных, классификация по типам имеет смысл лишь для этого решения. См. также Нелинейное уравнение с частными производными.
Когда Fпредставляет собой iV-мерный вектор F=(F1 , ...., FN )с компонентами
 зависящими от
зависящими от  и от M-мерных векторов
и от M-мерных векторов
векторное равенство (1) наз. системой дифференциальных уравнений с частными производными относительно неизвестных функций u1, ..., и М или относительно неизвестного вектора и=(u1, ..., и М). Максимальный порядок производных от искомых функций, входящих в данное уравнение системы, наз. порядком этой системы (уравнения). Когда M=N и порядок каждого уравнения системы (1) равен т, определитель

где
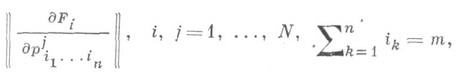
- квадратная матрица, представляет собой форму порядка Nm относительно действительных скалярных параметров l1, ...,l п и наз. характеристическим детерминантом системы (1). Классификация по типам системы (1) происходит по характеру формы (7) точно так же, как при рассмотрении одного уравнения порядка т. Фигурирующие в левой части уравнения (1) величины могут быть комплексными. Комплексное Д. у. с ч. п. очевидным образом заменяется системой Д. у. с ч. п.
Д. у. с ч. п. может вовсе не иметь решения. Однако встречающиеся в приложениях Д. у. с ч. п., как правило, имеют целые семейства решений. При выводе этих уравнений из общих законов, к-рым подчинены изучаемые явления природы, естественно возникают дополнительные условия, налагаемые на искомые решения. Центральное место в теории Д. у. с ч. п. занимают задачи отыскания именно таких регулярных решений, к-рые удовлетворяют этим условиям. Условия задач, к-рым должно удовлетворять искомое решение, существенно зависят от типа рассматриваемого уравнения.
Для эллиптич. уравнений обычно рассматриваются так наз. краевые задачи, к-рые, напр., в случае уравнения 2-го порядка в основном охватываются следующей постановкой: ищется регулярное в области Dрешение и(х)уравнения (1), удовлетворяющее условию

где S- граница области D, f и Н- заданные действительные функции, dst- элемент площади поверхности S, а под
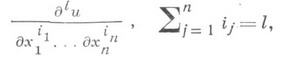
при xОSпонимаются пределы соответствующих производных функции и(х), когда точка хизнутри области Dстремится к S.
В такой общей постановке задача (8) далека от своего сколько-нибудь полного решения. Сравнительно хорошо исследованы такие частные случаи этой задачи, какими являются тал наз. первая и вторая краевые задачи (см. Дирихле задача и Неймана задача )для линейных уравнений, удовлетворяющих условию равномерной эллиптичности.
В отличие от краевых задач для эллиптич. уравнений, в к-рых носителем данных является вся граница области, где ищется решение, для широких классов уравнений гиперболич. и параболич. типов носителями дополнительных данных могут служить определенным образом ориентированные незамкнутые поверхности пространства Е n, причем от них существенно зависит область определения искомого решения. К таким задачам относятся, напр., Коши задача с начальными данными, характеристическая задача Коши" Особо ставятся краевые задачи для уравнений смешанного типа. В теории Д. у. с ч. п. значительное внимание уделяется обширному классу смешанных задач. См. Смешанная задача для гиперболического уравнения и системы. Смешанная и краевая задачи для параболического уравнения и системы.
Задача считается в классич. смысле корректно (правильно) поставленной, если она имеет и притом единственное устойчивое решение. Задачи, не удовлетворяющие этим требованиям, до недавнего времени считались лишенными смысла. Начиная с 40-х гг. 20 в. широта диапазона математич. проблем физики, механики и техники заставила расширить не только понятие корректности постановок задач для Д. у. с ч. п., но и понятие самого решения. Были введены так наз. обобщенные решения. Наряду с вопросами существования и единственности точных решений тех или иных задач для Д. у. с ч. п. в приложениях значительную важность приобрели понятия в определенном смысле приближенных решений и фактическое построение таких решений.
Исторически одним из первых методов, позволяющих строить решения ряда задач для важных классов Д. у. с ч. п., является метод разделения переменных, или Фурье метод, к к-рому тесно примыкает метод интегральных преобразований (см. Фурье интеграл). От применения этого метода берет свое начало спектральная теория дифференциальных операторов.
Сравнительно позже был создан параметрикса метод, на основе к-рого построен потенциалов метод. Этот метод позволяет привлекать к исследованию краевых задач для эллиптич. уравнений аппарат интегральных уравнений. Далеко идущим развитием метода параметрикса являются методы теории функций комплексного переменного, успешно применяющиеся при исследовании эллиптич. уравнений с двумя независимыми переменными. См. Дифференциальное уравнение с частными производными;методы комплексного переменного.
Когда изучаемое Д. у. с ч. п. представляет собой уравнение Эйлера для многомерной задачи вариационного исчисления, часто пользуются вариационным методом. Вариационный метод весьма удобен в тех случаях, когда уравнение Эйлера является уравнением эллиптич. типа. См. также Дифференциальное уравнение с частными производными;вариационные методы решения.
Начиная с 30-х гг. 20 в. при исследовании Д. у. с ч. п. широко используются методы функционального анализа, среди к-рых центральное место занимают Шаудера метод и его дальнейшее развитие - метод априорных оценок. Эти методы позволяют сравнительно легко установить существование слабых решений и сильных решений как для линейных, так и для нек-рых классов нелинейных Д. у. с ч. п. См. Дифференциальное уравнение с частными производными;функциональные методы решения.
Среди методов, успешно приводящих к цели при построении приближенных решений Д. у. с ч. п., чаще всего применяются методы конечных разностей исчисления. См. также Гиперболического типа уравнение, численные методы решения; Параболического типа уравнение, численные методы решения; Эллиптического типа уравнение, численные методы решения.
Лит.:[1] Берс Л., Джон Ф., Шехтер М., Уравнения с частными производными, пер. с англ., М., 1906; [2] Бицадзе А. В., Уравнения математической физики, М., 1976; [3] Владимиров В. С, Уравнения математической физики, 2 изд., М., 1971; [4] Курант Р., Уравнения с частными производными, пер. с англ., М., 1964; [5] Тихонов А. Н., Самарский А. А., Уравнения математической физики, 4 изд., М., 1972.
А. В. Бицадзе.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; вариационные методы решения - методы решения краевых задач для Д. у. с ч. п. при помощи сведения этих задач (когда это возможно) к соответствующим образом подобранным вариационным задачам (т. е. к задачам на отыскание минимума или максимума нек-рого функционала) и решения последних.
Вариационные методы широко применяются как в теоретич. исследованиях (для доказательства теорем существования, единственности и устойчивости решений, при исследовании дифференциальных свойств решений, в спектральной теории, при изучении разнообразных вопросов оптимизации и т. д.), так и в вопросах, связанных с нахождением приближенных решений уравнений. Приближенные решения вариационных задач можно находить при помощи решения конечных систем алгебраич. уравнений, при этом алгоритмы нахождения приближенных решений вариационных задач часто оказываются проще и удобнее, чем имеющиеся алгоритмы решения соответствующих задач для Д. у. с ч. п.
Вариационный метод исследования краевых задач возник в сер. 19 в. в виде так наз. Дирихле принципа отыскания в области Gгармонич. функции, принимающей на границе дG области Gданное значение j(x),
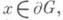 как функции, дающей в рассматриваемом классе функций минимум интегралу Дирихле. Первоначально принцип Дирихле применялся лишь в теории линейных эллиптич. уравнений 2-го порядка (впоследствии и более высоких порядков), а затем и в теории уравнений других типов, причем не только линейных, но и нелинейных. Разработке вариационных методов были посвящены работы Б. Римана (В. Riemann), К. Вейерштрасса (К. Weierstrass), Д. Гильберта (D. Hilbert). Большую роль в развитии вариационных методов, в частности в вопросе их обоснования, сыграли вложения теоремы и их обобщения.
как функции, дающей в рассматриваемом классе функций минимум интегралу Дирихле. Первоначально принцип Дирихле применялся лишь в теории линейных эллиптич. уравнений 2-го порядка (впоследствии и более высоких порядков), а затем и в теории уравнений других типов, причем не только линейных, но и нелинейных. Разработке вариационных методов были посвящены работы Б. Римана (В. Riemann), К. Вейерштрасса (К. Weierstrass), Д. Гильберта (D. Hilbert). Большую роль в развитии вариационных методов, в частности в вопросе их обоснования, сыграли вложения теоремы и их обобщения.Одним из простых и типичных примеров использования вариационных методов является решение Дирихле задачи для эллиптического самосопряженного уравнения 2-го порядка

где



(G- область конечномерного евклидова пространства, дG- ее граница, j - заданная на дG функция), и существует постоянная х>0 такая, что для всех точек
 и всех чисел x1, x2, ... , xn выполняется неравенство (условие эллиптичности)
и всех чисел x1, x2, ... , xn выполняется неравенство (условие эллиптичности)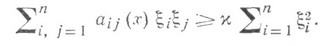
В этом случае вариационный метод решения задачи (1) - (2) состоит в отыскании функции и(х), для к-рой функционал

(уравнение (1) является Эйлера уравнением для функционала К(и))принимает наименьшее значение в классе допустимых функций, т. е. таких функций и(х), для к-рых
 и выполняется граничное условие (2). Вариационный метод применим только тогда, когда класс допустимых функций не пуст. Условия, к-рым должна удовлетворять заданная на границе функция j для того, чтобы класс допустимых функций был не пуст, даются теоремами вложения. Функция и(х), для к-рой функционал К(и)принимает наименьшее значение в классе допустимых функций, является обобщенным решением задачи (1) - (2) (см. Дифференциальное уравнение с частными производными;функциональные методы решения) и, напр., в классическом случае непрерывной дифференцируемости коэффициентов aij(x)оператора (3) - обычным решением этой задачи.
и выполняется граничное условие (2). Вариационный метод применим только тогда, когда класс допустимых функций не пуст. Условия, к-рым должна удовлетворять заданная на границе функция j для того, чтобы класс допустимых функций был не пуст, даются теоремами вложения. Функция и(х), для к-рой функционал К(и)принимает наименьшее значение в классе допустимых функций, является обобщенным решением задачи (1) - (2) (см. Дифференциальное уравнение с частными производными;функциональные методы решения) и, напр., в классическом случае непрерывной дифференцируемости коэффициентов aij(x)оператора (3) - обычным решением этой задачи.Другим типичным примером использования вариационных методов является их применение к отысканию собственных значений и собственных функций оператора (3).
Функция, дающая минимум нек-рому функционалу, может быть получена как предел так наз. минимизирующей последовательности, т. е. последовательности функций, значения функционала на членах к-рой стремятся к указанному минимуму. Для построения минимизирующих последовательностей и установления скорости их сходимости разработаны специальные методы (напр., Ритца метод).
Лит.:[1] Курант Р., Уравнения с частными производными, пер. с англ., М., 1964; [2] его же, Принцип Дирихле, конформные отображения и минимальные поверхности, пер. с англ., М., 1953; [3] Соболев С. Л., Некоторые применения функционального анализа в математической физике, Новосиб., 1962; [4] Смирнов В. И., Курс высшей математики, т. 3-5, М., 1958-59; [5] Михл ин С. Г., Вариационные методы в математической физике, 2 изд., М., 1970; [6] Ладыженская О. А., Уральцева Н. Н., Линейные и квазилинейные уравнения эллиптического типа, 2 изд., М., 1973; [7] Михайлов В. П., Дифференциальные уравнения в частных производных, М., 1976.
Л. Д. Кудрявцев.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; задача с данными на характеристиках - задача, состоящая в решении дифференциального уравнения или системы уравнений с частными производными по заданным условиям на характеристических многообразиях. Основными задачами такого типа являются характеристическая задача Коши и Гурса задача.
В случае характеристич. задачи Коши, когда начальное многообразие является характеристич. в каждой точке, начальные данные не могут быть заданы произвольным образом. Они должны удовлетворять определенным условиям, к-рые диктуются дифференциальным уравнением. Поэтому характеристич. задача Коши, вообще говоря, не является корректно поставленной, если на класс искомых решений и на заданные функции не наложены дополнительные условия (особенно вдоль многообразия, не касательного к начальному). Напр., для теплопроводности уравнения

характерпстич. задача Коши

корректна в классе функций, растущих на бесконечности не быстрее ехр( сх 2);если же показатель 2 при хзаменить на 2+e, то единственности уже не будет. Существует широкий класс уравнений, для к-рых характеристич. задача Коши корректна.
Если начальное многообразие Sодновременно является многообразием вырождения типа или порядка уравнения, хр характеристич. задача может оказаться правильно поставленной. Напр., для уравнения
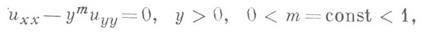
с достаточно гладкими начальными данными на любом интервале Sхарактеристики у=0 задача разрешима и притом единственным образом.
К задачам с данными на характеристиках относятся задачи с неполными и видоизмененными начальными данными, к-рые возникают в теории вырождающихся гиперболич. и параболич. уравнений и систем. Эти задачи для уравнений вида

ставятся следующим образом. Требуется отыскать решение и( х, у )уравнения, удовлетворяющее видоизмененным начальным данным

где a<x<b, j, t, y и v - заданные функции, или неполным начальным данным, т. е. одному из этих условий.
Лит,:[1] Бицадзе А. В., Уравнения смешанного типа, М., 1959; [2] Курант Р., Уравнения с частными производными, пер. с англ., М., 1964; [3] Тихонов А. Н., "Матем. сб.", 1935, т. 42, с. 199-216; [4] Xермандер Л., Линейные дифференциальные операторы с частными производными, пер. с англ., М., 1965; [5] его же, "Математика", 1968, т. 12, № 2, с. 88 - 109.
А. М. Нахушев.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; задача с косой (наклонной) производной - лгпге:гаая краевая задача для эллиптич. уравнений 2-го порядка.
Пусть D - область действительного евклидова пространства с декартовыми координатами x1, х 2,. . ., х п, граница дD к-рой представляет собой (п-1)-мерную гиперповерхность Ляпунова. Пусть в области Dзадано линейное дифференциальное уравнение 2-го порядка

с действительными коэффициентами а ij, bi, с, F, удовлетворяющими условию Гёльдера в
 и, кроме того, в Dсоблюдено условие равномерной эллиптичности уравнения. Пусть l=(l1, l2, ..., ln)- заданный на дD непрерывный действительный вектор, к-рый нигде не обращается в нуль. Задача с косой производной состоит в следующем: найти регулярное в области Dрешение и(х)уравнения (1), непрерывное в
и, кроме того, в Dсоблюдено условие равномерной эллиптичности уравнения. Пусть l=(l1, l2, ..., ln)- заданный на дD непрерывный действительный вектор, к-рый нигде не обращается в нуль. Задача с косой производной состоит в следующем: найти регулярное в области Dрешение и(х)уравнения (1), непрерывное в  для к-рого в каждой точке
для к-рого в каждой точке  существует предел
существует предел
совпадающий с заданной непрерывной на дD функцией f(y)
f(y):

В краевом условии (2) без ограничения общности можно считать, что l- единичный вектор. Неймана задача является частным случаем задачи с косой производной, когда левая часть в краевом условии (2) совпадает с производной от искомого решения по конормали v:

Если соблюдены условия

и

где N- внешняя нормаль дD в точке у, то соответствующая задаче (1), (2) однородная краевая задача

в силу принципов Хопфа и Зарембы - Жиро (см., напр., [1]), не может иметь решения, отличного от постоянной. В частности, когда в условии (3) по крайней мере в одной точке выполняется строгое неравенство, задача (1), (2) не может иметь более одного решения. При исследовании вопроса о существовании решений задачи (1), (2) обычно пользуются методом интегральных уравнений, априорными оценками или методами конечных разностей исчисления.
Выполнение условия (4) гарантирует фредгольмовость задачи (1), (2), то есть: а) размерность x1 пространства решений однородной задачи (5) конечна; б) если х 1=0, то задача (1), (2) всегда разрешима и притом однозначно; если х 1>0, то существует пространство линейных функционалов, обращение в нуль к-рых над Fи f является условием, необходимым и достаточным для существования решений задачи (1), (2); причем размерность этого пространства также равна х 1. Фредгольмовость задачи (1), (2) может нарушиться лишь тогда, когда множество Мточек у, для к-рых (Nl) = 0, не пусто. В частности, при п = 2 в предположении, что

(а это не ограничивает общность), задача (1), (2) редуцируется к эквивалентному сингулярному интегральному уравнению с ядром Коши, откуда следует нетеровость задачи, то есть: а) размерность х 1 пространства решений однородной задачи (5) конечна; б) размерность х 2 пространства линейных функционалов, обращение в нуль к-рых над Fи f является условием, необходимым и достаточным для разрешимости задачи (1), (2), также конечна; в) разность х 1 -х 2=x (индекс задачи (1), (2)) дается формулой

где 2яр - приращение arg(l1-l2) при однократном обходе контура 3D области Dв положительном направлении. В рассматриваемом случае задача (1), (2) будет фредгольмовой лишь при р=-1. Число рхарактеризует вращение векторного поля (l1, l2) Когда (1) представляет собой равномерно эллиптич. систему, т. е. когда Fи иявляются ткомпонентными векторами, а а ij, bi, и с- квадратными матрицами порядка т, причем матрицы а ij удовлетворяют

условию при определении оператора l(и). в краевом условии (2) задачи с косой производной под l1, l2, ..., l п следует понимать квадратные матрицы порядка т, а под f- вектор с ткомпонентами.
Нётеровость задачи с косой производной имеет место для широких классов равномерно эллиптич. систем и операторов l(и). Так, напр., когда п=2 и а ij=0, i неравно j, а ii=Е, где Е- единичная (диагональная) матрица, выполнение условия
 всюду на дD гарантирует нётеровость задачи (1), (2). При соблюдении этого условия индекс задачи (1), (2) вычисляется по формуле х=2 (р+m), где 2pp - приращение arg det(l- il2). при однократном обходе контура 3D области Dв положительном направлении.
всюду на дD гарантирует нётеровость задачи (1), (2). При соблюдении этого условия индекс задачи (1), (2) вычисляется по формуле х=2 (р+m), где 2pp - приращение arg det(l- il2). при однократном обходе контура 3D области Dв положительном направлении.С 60-х гг. 20 в. ведется интенсивное исследование задачи с косой производной при
 (см. [1]).
(см. [1]).Лит.:[1] Бицадзе А. В., Краевые задачи для эллиптических уравнений второго порядка, М., 1966; [2] Векуа И. Н., Обобщенные аналитические функции, М., 1959; [3] Мусхелишвили Н. И.. Сингулярные интегральные уравнения, 3 изд., М., 1968; [4] Воuligand G., Giraud G., Delens P., Le probleme de la derivee oblique en theore du potentiel, P., 1935.
А. В. Бицадзе.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; задача с разрывными коэффициентами - задача для Д. у. с ч. п., в к-рой коэффициенты дифференциальных операторов испытывают разрывы 1-го рода (или скачки) при переходе через нек-рые поверхности и на этих поверхностях заданы условия сопряжения.
Задала с разрывными коэффициентами в случае эллиптич. операторов 2-го порядка (задача трансмиссии) состоит в следующем. В произвольной ограниченной открытой N-мерной области gс границей Г задана (N-1)-мерная поверхность Г 1, разбивающая область gна подобласти g1 и g2;в области (g+ Г) ставится задача:

где

- определенный в области gl линейный дифференциальный оператор эллиптич. типа;

где д/дvl- производная по конормали, равная
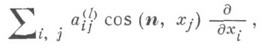
п- внешняя нормаль к Г 1, а символы Г 1-0 и Г 1+0 означают, что берутся предельные значения соответственно с внутренней и с внешней сторон поверхности Г 1 по отношению к области g1, fl,j, y, c - заданные функции.
Здесь для простоты считается, что имеется лишь одна поверхность разрыва коэффициентов - поверхность Г 1.
Задача (*) является математич. описанием стационарных физич. процессов, происходящих в области, составленной из различных сред, напр, рассеяния электромагнитной волны на каком-либо препятствии или распространения тепла в слоистой среде.
У задачи (*) существует классич. решение при условиях, к-рые в случае отсутствия разрыва у коэффициентов и при j=y=0 переходят в Жиро условия разрешимости задачи Дирихле (см. [3], [4], [5]). Для задачи (*) изучались: обобщенные из Wl2 решения (см. [1], [2]); задача на собственные значения и оценки собственных функций для самосопряженных операторов Ll (см. [6], [8]); случаи вырождения в связи с марковскими процессами (см. [9], [10]); случаи с квазилинейными операторами Ll (см. [13]). Для задачи (*) могут быть установлены оценки Шаудера (см. [6], [7]); разработаны численные методы ее решения [11], [12]. Построена теория разрешимости задач с разрывными коэффициентами для эллиптич. уравнений и систем порядка 2т (см. [18], [19], [20]).
Задача с разрывными коэффициентами для параболич. и гиперболич. операторов 2-го порядка столь же подробно изучена (см. [2], [9], [14], [15], [16], [17]).
Лит.:[1] Ладыженская О. А., "Докл. АН СССР", 1954, т. 96, № 3, с. 433-36; [2] Олейник О. А., "Изв. АН СССР. Сер. матем.", 1961, т. 25, № 1, с. 3-20; [3] Ильин В. А., Шишмарев И. А., "Сиб. матем. ж.", 1961, т. 2, № 1, с. 46 - 58; [4] Ильин В. А., "Докл. АН СССР", 1961, т. 137, Х" 1, с. 28-30; [5] Ладыженская О. А., Уральцева Н. И., Линейные и квазилинейные уравнения эллиптического типа, М., 1964; [6] Шишмарев И. А., "Докл. АН СССР", 1961, т. 137, № 1, с. 45-47; [7] В ан Тун, "Ж. вычисл. матем. и матем. физ.", 1964, т. 4, №3, с. 577-80; [8] Ильин В. А., "Докл. АН СССР", 1961, т. 137, № 2, с. 272-75; [9] Гирсанов И. В., "Докл. АН СССР", 1960, т. 135, № 6, с. 1311 - 13; [10] Фрейдлин М. И., "Докл. АН СССР", 1962, т. 144, № 3, с. 501-04; [11] Самарский А. А., в кн.: Тр. 4-го Всесоюзного матем. съезда. Ленинград, 1961, т. 2, Л., 1964; [12] его же, "Ж . вычисл. матем. и матем. физ.", 1961, т. 1, №3, с. 441 - 460; [13] Борсук М. В.,"Докл. АН СССР", 1967, т. 177, № 5, с. 991-94; [14] Камынин Л. И., в кн.: Материалы к совместному советско-американскому симпозиуму по уравнениям с частными производными, Новосиб., 1963, с. 3-6; [15] Камынин Л. И., Масленникова В. Н., "Сиб. матем. ж." 1961, т. 2, № 3, с. 384-99; [16] Ильин В. А., "Докл. АН СССР", 1962, т. 142, Х° 1, с.21 - 4; [17] Егоров Ю. В., "Докл АН СССР", 1960, т. 134, Д. 3, с. 514-17; [18] SchechterM., "Ann. Scuola norm, super. Pisa. Sci. fis. e mat.", I960, v 14 p. 207-36; [19] Ройтберг Я. A., Шepтель З. Г., "Докл. АН СССР", 1963, т. 148, № 5, с. 1034-37; [20] их же, "Успехи матем. наук", 1967, т. 22, в. 5, с. 181-82.
И. А. Шишмарев.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; задача с разрывными начальными (краевыми) условиями - задача для Д. у. с ч. п., в к-рой функции, задающие (начальные) краевые условия, не являются непрерывными.
Пусть, например, для гиперболического уравнения второго порядка

поставлена смешанная задача с начальными условиями:
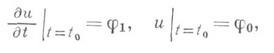
и краевыми условиями

в этом смысле разрывы начальных функций j0 и j1 влекут за собой разрывы ии дu/дt вдоль характеристических лучей х-at=const и x+at=const, причем мера разрыва

или

где
 - точка разрыва функций j0 или j1,
- точка разрыва функций j0 или j1,удовлетворяет вдоль характеристического луча уравнению
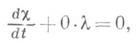
т. е. x=const- Аналогичные результаты справедливы для гиперболических уравнений 2-го порядка с переменными коэффициентами:

В этом случае разрывы начальных функций и краевых условии также влекут за собой разрывы ии du/dt вдоль характеристических лучей, определяемых из системы уравнений

мера разрыва cудовлетворяет уравнению:

где функция j(х)определяет характеристическую поверхность в виде уравнения j(x)=С.
Для уравнения эллиптического типа разрывы краевых условий внутрь области Dне распространяются, т. к. в этом случае характеристические лучи комплексны. Для таких уравнений эллиптического типа изучен вопрос о существовании и единственности решения и об удовлетворении решения граничным условиям. Так, для эллиптических уравнений 2-го порядка в произвольной области

доказано, что если граничная функция
 для первой краевой задачи и
для первой краевой задачи и  для второй краевой задачи, то существует обобщенное решение из
для второй краевой задачи, то существует обобщенное решение из  к-рое удовлетворяет граничному условию
к-рое удовлетворяет граничному условиюв среднем, т. е.
 где поверхности дDn аппроксимируют поверхность дD. В случае параболических уравнений (также как и для эллиптических уравнений) разрывы внутрь области Dне распространяются, если разрывны начальные данные или краевые условия. Для этих задач изучены также вопросы о существовании и единственности обобщенного решения граничному условию.
где поверхности дDn аппроксимируют поверхность дD. В случае параболических уравнений (также как и для эллиптических уравнений) разрывы внутрь области Dне распространяются, если разрывны начальные данные или краевые условия. Для этих задач изучены также вопросы о существовании и единственности обобщенного решения граничному условию.Лит.:[1]Тихонов А. Н., Самарский А. А., Уравнения математической физики, 4 изд.,М., 1972; [2] Владимиров В. С, Уравнения математической физики, М., 1976; [3] Бицадзе А. В., Уравнения математической физики, М., 1976; [4] Курант Р., Уравнения с частными производными, пер. с англ., М., 1964; [5] Берс Л., Джон Ф., Шехтер М., Уравнения с частными производными, пер. с англ., М., 1966; [6] Ладыженская О. А., Уральцева Н. Н., Линейные и квазилинейные уравнения эллиптического типа.
2 изд., М., 1973; [7] Ладыженская О. А., Солонников В. А.,Уральцева Н. Н., Линейные и квазилинейные уравнения параболического типа, М., 1967; [8] Фридман А., Уравнения с частными производными параболического типа, пер. с англ., М., 1968; [9] Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., М., 1957; [10] Агмон С, Дуг лис А., Ниренберг Л., Оценки решений эллиптических уравнений вблизи границы ..., пер. с англ., М., 1962.
Е. И. Моисеев.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; задача со свободными границами - задача, в к-рой требуется найти решение системы Д. у. с ч. п. с соответствующими начальными и граничными условиями в области, граница к-рой частично или полностью неизвестна и подлежит определению.

К такого типа задачам приводят многие проблемы фильтрации, диффузии, теплопроводности и др. разделов механики сплошных сред. Так, напр., задача Гельмгольца - Кирхгофа о симметричном струйном обтекании равнобочного клина с углом раствора 2ая неограниченным потоком идеальной жидкости заключается в отыскании компонент скорости и=и( х, у), v=v(x, у), являющихся решением системы уравнений Коши - Римана:

и удовлетворяющих на известной границе условиям (см. рис.):

Неизвестная граница BS является линией тока, и на ней задано дополнительное условие

(на рис. приведена верхняя половина течения
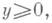 при
при  течение симметрично).
течение симметрично).При изучении плоских задач со свободными границами большую роль играют методы теории функций комплексного переменного.
См. также Стефана задача.
Лит.:[1] Монахов В. Н., Краевые задачи со свободными границами для эллиптических систем, Новосиб., 197 7; [2] Кружков С. Н.,"Прикл матем. и механ.", 1967, т. 31, в. 6, с. 1009-20; [3] Шишкин Г. И., "Докл. АН СССР", 1971, т. 197, № 6, 1276-79.
Ф. П. Васильев
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; метод уравнений Фишера - Рисса, метод Пикон е,- метод решения краевых задач для Д. у. с ч. п., основанный на применении формулы Грина и приводящий к системе интегральных уравнений (Фишера - Рисса) .для нек-рого подходящим образом подобранного неизвестного вектора. Метод дает возможность находить численные значения решений, но может быть применен и для доказательства теорем существования.
Пусть L* и L- сопряженные линейные эллиптические операторы 2-го порядка в пространстве точек ( х и х 2, ..., х п )с действительными коэффициентами

D- конечная область, ограниченная замкнутой поверхностью S. Пусть в классе функций, допускающих интегральные представления по формулам Грина, ищется решение и(х)задачи Дирихле:

Пусть, далее, v(x)- произвольная функция из того же класса. Применение формулы Грина к и(х)и v(x). приводит к соотношению где


v - внутренняя конормаль. Пусть U-( и 1, и 2 )-двухкомпонентный вектор, составляющие к-рого -действительные функции с суммируемым квадратом, причем первая составляющая определена в D, а вторая - на S. Пусть L2(D, S) - множество этих векторов; норма вводится через скалярное произведение Uи Vиз L2(D, S):

Пусть {vk}- множество, выбранное так, что совокупность двухкомпонентных векторов

полна в гильбертовом пространстве L2(D, S). Тогда, обозначив через U -(u1, и 2 )вектор с первой составляющей u1 (х), равной u(x), и второй составляющей и 2 (у), совпадающей с дu/дv, можно записать (1) в виде системы интегральных уравнений Фишера - Рисса:

Если совокупность {Vk} ортонормирована и выполняются условия Рисса- Фишера теоремы, то система (2) определит в L2(D, S )коэффициенты Фурье ck вектора U= (u1, u2 )относительно полной системы базисных векторов , {Vk}. Если известно, что решение рассматриваемой задачи существует и единственно, то ряд Фурье
 сходится в среднем к искомому решению и только к нему. В противном случае выбор функций {vk} связан с необходимостью дополнительного исследования. Так, если допускаются собственные решения и 0 (х)(нарушена единственность), совокупность {Vk} должна удовлетворять равенствам
сходится в среднем к искомому решению и только к нему. В противном случае выбор функций {vk} связан с необходимостью дополнительного исследования. Так, если допускаются собственные решения и 0 (х)(нарушена единственность), совокупность {Vk} должна удовлетворять равенствам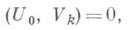
где U0=(u0 (х), дu0/dv). Если в качестве {vk} взята последовательность одночленов
 с целыми неотрицательными показателями a1, a2, ..., a т, то значения и(х)и дu/дv, найденные из (2), вместе с заданным йа Sзначением и(х), удовлетворяют функциональным соотношениям Грина:
с целыми неотрицательными показателями a1, a2, ..., a т, то значения и(х)и дu/дv, найденные из (2), вместе с заданным йа Sзначением и(х), удовлетворяют функциональным соотношениям Грина:
где k т- отличная от нуля постоянная, зависящая от т, и w(y, x)- фундаментальное решение уравнения L*v=0. В этом случае все решения системы уравнений Фишера - Рисса (2) и только они являются решениями рассматриваемой краевой задачи. Центральным пунктом этого метода является построение подходящим образом выбранной совокупности функций {vn}, удовлетворяющих условию L*vn=0 либо нек-рым условиям полноты [4].
Этот способ не требует задания явного выражения фундаментального решения, но если последнее известно, то, в силу того, что совокупность {w(y, x{k))}, где x(k)- счетная бесконечная последовательность произвольных точек, не принадлежащих DUS, линейно независима и полна в L2(S)[4], можно значительно упростить вычисления; эта теорема позволяет также распространить метод уравнений Фишера - Рисса на задачи с косыми производными (см. Дифференциальное уравнение с частными производными;задача с косой производной) и другие типы уравнений.
Лит.:[1] Picone M., "Atti Accad. sci. Torino. Cl. sci. fis., mat. e natur.", 1940, v. 75, p. 413-26; [2] Ameriо L., "Amer. J. Math.", 1947, v. 69, №3, p. 447-89; [3] Fiсhera G., "Ann. Scuola norm, super. Pisa. Sci. fis. e mat.", 1950, t. 4, fase. 1-2, p. 35-99; [4] Купрадзе В. Д., "Успехи матем. наук", 1967, т. 22, в. 2, с. 59-107; [5] Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., М., 1957.
В. Д. Купрадзе.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; методы комплексного переменного - методы решения эллиптических Д. у. с ч. п., в к-рых используется представление решений через аналитич. функции комплексного переменного.
Теория аналитич. функций

комплексного переменного z=x+iy представляет собой теорию двух действительных функций и( х, у )и v(x, у), удовлетворяющих системе уравнений Коши - Римана: и х-vy=0, uy+vx=0, к-рая по существу эквивалентна уравнению Лапласа

Начиная с 30-х гг. 20 в. методы аналитич. функций интенсивно стали проникать в общую теорию уравнений эллиптич. типа. Это привело к созданию нового раздела анализа, существенно расширяющего рамки классич. теории аналитич. функций и ее применений. В этой области фундаментальную роль играют различные формулы представления всех решений весьма широкого класса эллиптич. уравнений через аналитич. функции одного комплексного переменного. Для линейных уравнений эти представления осуществляются с помощью нек-рых линейных операторов, выражающихся посредством коэффициентов. Эти формулы дают возможность распространить свойства аналитич. функций на решения уравнений эллиптич. типа, причем, в ряде случаев в дословной формулировке сохраняются такие важные свойства, как теорема единственности, принцип аргумента, теорема Лиувилля и др. В естественной форме обобщаются ряды Тейлора и Лорана, интегральная формула Коши, принцип компактности, принцип аналитич. родолжения и др.
Формулы комплексного представления позволяют строить разнообразные семейства частных решений уравнения, обладающие теми или иными заданными свойствами. Напр., можно строить различные классы так наз. элементарных решений, имеющих точечные особенности, к-рые используются для получения различных интегральных формул, а также так наз. полные системы частных решений; последние обладают тем свойством, что при помощи их линейных комбинаций можно приближать любые решения. Формулы комплексного представления позволяют также редуцировать широкий круг граничных задач к эквивалентным краевым задачам для аналитич. функций, а также строить эквивалентные задаче интегральные уравнения (типа Фредгольма или сингулярные). Этот метод позволяет исследовать краевые задачи нефредгольмового типа, получить условие нормальной разрешимости и явную формулу индекса. См. Краевая задача;методы комплексного переменного.
Эллиптические уравнения с аналитическими коэффициентами. Пусть дано уравнение 2-го порядка эллиптич. типа

где а, b и с - аналитич. функции действительных переменных х, у в нек-рой области плоскости z=x+iy. Аналитическое продолжение коэффициентов в область независимых комплексных переменных z=x+iy,z = х- iy приводит уравнение (1) к виду:
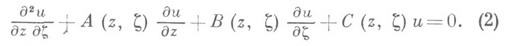
Односвязная область D0 наз. основной областью уравнения (1), если А, В и С- аналитич. функции двух независимых переменных в цилиндрич. области (D0, D0), где D0 обозначает зеркальное изображение D0 относительно действительной оси.
Если
 - односвязная область, то все регулярные в области Dрешения уравнения (1) выражаются по формуле
- односвязная область, то все регулярные в области Dрешения уравнения (1) выражаются по формуле
где Ф(z) - произвольная голоморфная функция в области
 - произвольные фиксированные точки; аналитич. функция G(z,z, t,t) четырех независимых комплексных аргументов в цилиндрич. области
- произвольные фиксированные точки; аналитич. функция G(z,z, t,t) четырех независимых комплексных аргументов в цилиндрич. области  наз. функцией Римана уравнения (1). Она является решением интегрального уравнения типа Вольтерра:
наз. функцией Римана уравнения (1). Она является решением интегрального уравнения типа Вольтерра:
Осуществляемое формулой (3) соответствие между семейством решений {и} уравнения (1) и семейством голоморфных функции {Ф} взаимно однозначно, если зафиксировать значения мнимой части Ф в фиксированной точке zx области D. При z1 = z0=0 имеет место формула обращения:
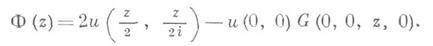
Уравнение (4) можно решить методом последовательных приближений. Таким путем можно найти приближенные выражения для функции Римана.
В случае многосвязной области Dформула (3) дает, вообще говоря, многозначные решения. Чтобы получить в этом случае все однозначные решения уравнения (1), в качестве Ф в (3) надо брать многозначные функции определенного вида.
Пусть D- двухсвязная область (
 ), D' - ограниченный континуум, дополняющий Dдо односвязной области. Тогда все однозначные в области Dрешения уравнения (1) даются формулой
), D' - ограниченный континуум, дополняющий Dдо односвязной области. Тогда все однозначные в области Dрешения уравнения (1) даются формулой
где
 - фиксированные точки, ф (z) - многозначная аналитич. функция вида
- фиксированные точки, ф (z) - многозначная аналитич. функция вида
Здесь а - произвольная действительная постоянная, Ф 0(z) - произвольная голоморфная функция в области D, L- любая простая замкнутая кусочно гладкая кривая, лежащая в Dи окружающая D'. Функции Ни Н* выражаются по формулам

Комплексные представления вида (3) распространяются также и на системы уравнений, записываемых в векторной форме в виде (1), где и- вектор с компонентами и 1,..., и п, а, b, с- квадратичные матрицы порядка и, элементы которых - аналитич. функции переменных х, у.
В той области, где уравнение (1) имеет хотя бы одно положительное решение u0>0, подстановкой u=u0v его можно привести к виду

(такое решение всегда существует в малой окрестности любой фиксированной точки, а также в любой области, где
 ). В этом случае уравнение (1) эквивалентно системе уравнений, к-рая представляет собой частный случай обобщенной системы Коши - Римана вида
). В этом случае уравнение (1) эквивалентно системе уравнений, к-рая представляет собой частный случай обобщенной системы Коши - Римана вида
Вводя в рассмотрение комплексную функцию w=u+iv, эту систему можно записать в виде

Если коэффициенты Аи В- аналитич. функции комплексных аргументов z и z(z=x+iy,z=x-iy )в нек-рой цилиндрич. области (D0, D0), где D0- односвязная область, то решение уравнения (6) в односвязной области
 выражается формулой
выражается формулой
в к-рой Г 1 и Г 2 - аналитич. функции своих аргументов, выражающиеся через А и В;они строятся по методу последовательных приближений, Ф - произвольная аналитич. функция переменного z.
В случае, когда Аи В- целые функции переменных x и y, представление (8) имеет место Для любой односвязной области плоскости z без ограничений па поведение коэффициентов Аи Ввблизи бесконечности.
Пусть дано эллиптич. уравнение вида

где
 - аналитич. функции х, у. Если D0- основная область уравнения (9), то всякое регулярное решение этого уравнения в односвязной области DМ D0, выражается формулой
- аналитич. функции х, у. Если D0- основная область уравнения (9), то всякое регулярное решение этого уравнения в односвязной области DМ D0, выражается формулой
где Ф 0, ..., Ф n-1 -произвольные голоморфные в области Dфункции

Здесь G- комплексная функция Римана уравнения (9), к-рая аналитически зависит от комплексных аргументов (t, t, z, z) в цилиндрич. области
 При выполнении условий
При выполнении условий
формула (10) осуществляет взаимно однозначное соответствие между семейством решений {и} уравнения (9) и семейством голоморфных функций {(Ф 0, ..., Ф n-1)}. Если D- многосвязная область, то формула (10) дает, вообще говоря, многозначные решения. Но, как и в случае уравнения 2-го порядка, можно видоизменить эту формулу так, чтобы она давала все однозначные решения уравнения (9) и в многосвязной области. Формула (10) распространяется также на, систему уравнений вида (9), где и - вектор, а коэффициенты - матрицы.
продолжение ДУ с частными производными..
Для ряда уравнений математич. физики функция Римана выражается в явной форме при помощи элементарных или специальных функций.
В случае уравнения колебаний мембраны

где J0 - функция Бесселя нулевого порядка; в качестве основной области можно взять всю комплексную плоскость. Случай l=0 дает уравнение Лапласа Du=0; тогда G=1 и формула (3) принимает вид
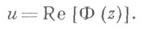
Для уравнения сферич. функций

где Р п - функция Лежандра первого рода; в качестве основной области можно взять любую односвязную область D0, для к-рой выполняется условие: если
 то
то  (напр., круг |z|<l). Для уравнения Эйлера - Дарбу
(напр., круг |z|<l). Для уравнения Эйлера - Дарбу
где 2b = a' + ia, 2b' = a' -ia, F- гипергеомётрич. ряд, в качестве основной области можно взять полуплоскости у>0 или у<0.
Для уравнения

и имеет место формула Гурса

Метод комплексных представлений решений применим также к пек-рому классу нелинейных уравнений. Пусть, напр., дано известное в дифференциальной геометрии уравнение Гаусса

тде ( х, у)- заданная функция. Если v0(z) - какое-либо частное решение этого уравнения, то его же решениями являются функции вида

где Ф (z) - произвольная аналитич. функция. Если k=const, то
 и все решения уравнения
и все решения уравненияГаусса выражаются формулой:

Если k<0, то надо предполагать, что |Ф (z)| <-k-1. Эллиптические уравнения с неаналитическими коэффициентами. Пусть дана обобщенная система уравнений Коши - Римана (7) с коэффициентами Аи В, заданными на всей плоскости Екомплексного переменного z и принадлежащими классу Lp, 2(E), т. е.

Если коэффициенты заданы в ограниченной области Sи принадлежат классу Lp(S), p>2, то они будут удовлетворять предыдущим условиям при продолжении их вне Sнулем. При этих предположениях уравнение (7), вообще говоря, не имеет решения в классическом смысле. Поэтому рассматриваются так наз. обобщенные решения: функция w(z)О L1(S). наз. решением уравнения (7) в области S, если она обладает производной в смысле С. Л. Соболева д zW О L1(S). и удовлетворяет уравнению почти везде в S.
Теория функций, удовлетворяющих уравнению (7), представляет собой далеко идущее обобщение классич. теории аналитич. функций (A=В=0) и сохраняет существенные черты последней. Поэтому решения уравнения вида (7) наз. обобщенными аналитическими функциями.
Всякое решение уравнения (7) (в S)удовлетворяет интегральному уравнению

где z=z+ih, Ф(z) - голоморфная функция в S. Если ФОLq(S),
 p>2, то уравнение (11) имеет единственное решение, к-рое выражается формулой вида
p>2, то уравнение (11) имеет единственное решение, к-рое выражается формулой вида
Резольвенты Г 1 и Г 2 зависят от коэффициентов уравнения (7) и строятся при помощи процесса последовательных приближений.
Формула (12) дает общее (линейное) представление решений уравнения (7) через аналитич. функции Ф (z). Она, в частности, позволяет построить так наз. основные ядра

тде t- некоторая фиксированная точка, а Х 1 и Х 2- решения интегрального уравнения (11), соответствующие функциям
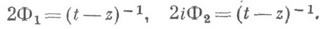
Эти ядра позволяют написать обобщенную формулу Коши:
 (13)
(13)При A=B=0 она обращается в классич. формул Коши. При помощи формулы (13) на обобщенные аналитич. функции распространяются многие из тех свойств аналитич. функций, к-рые доказываются обычно с помощью формулы Коши. В частности, можно обобщить классич. теоремы об аналитич. родолжении построить теорию обобщенных интегралов типа Коши получить представления обобщенных аналитич. функций в виде контурных интегралов с действительно плотностью и др.
Основными ядрами сопряженного уравнения
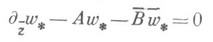 (14)
(14)являются функции

Если wи w* удовлетворяют в Sуравнениям (7) и (14), соответственно и непрерывны в S, то имеет место тождество (аналог классической теоремы Коши):

Если w(z) - решение уравнения (7) в области S, то существует такая аналитическая в Sфункция Ф(z), что имеет место равенство
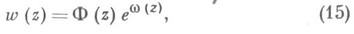
где

и принадлежит классу С a (Е),a=р/ (р-2), причем
 если
если 
Эта формула, в частности, позволяет распространить на решения уравнений вида (7) основные теоремы классич. теории аналитич. функций: теорему единственности, теорему Лиувилля, принцип аргумента, принцип компактности и др. Формула (15) допускает обращение: задавая аналитич. функцию Ф, можно найти функцию w(z), удовлетворяющую нелинейному интегральному уравнению (15).
Пусть Ф (z)- аналитическая в области Sфункция, к-рая может иметь любые особенности, и t- фиксированная точка. Тогда существует решение w(z)уравнения (7) такое, что функция w0=w/ Фнепрерывно продолжима на всю плоскость Е, принадлежит классу С a (Е), а-( р-2)/р, не обращается в нуль нигде на плоскости Еи w0(t)=1. Функция w0 удовлетворяет интегральному уравнению

к-рое имеет единственное решение, а функция w=Ф(z)w0 удовлетворяет нелинейному интегральному уравнению

из к-рого при
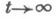 получается представление (15).
получается представление (15).Проблема приведения эллиптич. уравнения 2-го порядка общего вида
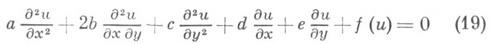
к виду (1) эквивалентна задаче редукции к канонич. виду
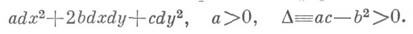
положительной квадратичной формы.
Последняя проблема эквивалентна отысканию гомеоморфизмов уравнения Бельтрами

где
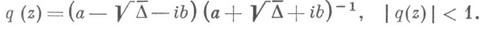
Если (19) - равномерно эллиптич. уравнение

При изучении уравнения Бельтрами основным вопросом является построение нек-рого его гомеоморфизма для данной области 5; если w(z) - гомеоморфизм уравнения Бельтрами, реализующий топологич. отображение области Sна область w(S), то всякое другое его решение в Sимеет вид

где Ф - произвольная аналитич. функция в области w(S).
Если q(z)- измерима, q(z)=0 вне S и |q(z)| <q0<1, то уравнение Бельтрами (20) имеет решение вида

где р удовлетворяет сингулярному интегральному уравнению (интеграл понимается в смысле главного значения по Коши):

Это уравнение имеет единственное решение в нек-ром классе Lp(E), р>2; его можно получить методом последовательных приближений. Функция (22) принадлежит классу С a (Е),a=р/(р-2), реализует топологич. отображение плоскости на себя, причем w(
 )=
)=
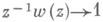 при
при  Если
Если  0<a<1,
0<a<1, то
то 
Равномерно эллиптич. система 1-го порядка общего вида в комплексной записи имеет вид

С помощью гомеоморфизма нек-рого уравнения вида (20) ее можно привести к виду (7).
Всякое решение уравнения (24) в нек-рой ограниченной области Sпри условии, что
 р>2, представлено в виде
р>2, представлено в виде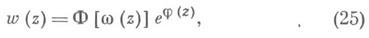
где w(z) - некоторый гомеоморфизм уравнения Бельтрами (20) с коэффициентом

Ф(w) - аналитич. функция в области w(S), функция
 a= (р-2)/р голоморфна вне S и исчезает на бесконечности. Представление (25) имеет место и тогда, когда коэффициенты левой части уравнения (24) зависят от wи ее производных любого порядка, лишь бы на рассматриваемых решениях выполнялись указанные выше условия. Как и (15), формула (25) допускает обращение.
a= (р-2)/р голоморфна вне S и исчезает на бесконечности. Представление (25) имеет место и тогда, когда коэффициенты левой части уравнения (24) зависят от wи ее производных любого порядка, лишь бы на рассматриваемых решениях выполнялись указанные выше условия. Как и (15), формула (25) допускает обращение.Формула (25) позволяет перенести целый ряд свойств классич. теории аналитич. функций на решения уравнения (24); теорему единственности, принцип аргумента, принцип максимума и др.
Общее квазиконформное отображение Qявляется решением нек-рой равномерно эллиптич. системы вида (24) (при A=B=0). Справедливо и обратное утверждение. Поэтому указанные выше результаты позволяют решить чисто аналитич. утем основные проблемы квазиконформных отображений.
Системы уравнений 1-го порядка эллиптич. типа с 2n, n>1, неизвестными функциями двух независимых переменных, при нек-рых естественных ограничениях, приводятся к канонич. виду:
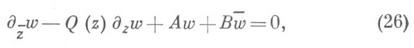
где w- искомый вектор с пкомплексно значными компонентами, Q, А, В- квадратные матрицы порядка п. Теория уравнений вида (26) имеет много сходства со случаем n=1, но она имеет и свои особенности.
Лит.:[1] Векуа И. Н., Новые методы решения эллиптических уравнений, М.- Л., 1948; [2] его же, Обобщенные аналитические функции, М., 1959; [3] его же, "Матем. сб.", 1952, т. 31, JM5 2, с. 217-314; [4] Бергман С, Интегральные операторы в теории линейных уравнений с частными производными, пер. с англ., М., 1964; [5] Веrs L., Theory of pseudoanalytic functions, N. Y., 1953; [6] Боярский Б. В., "Докл. АН СССР", 1958, т. 122, №4, с. 543-46; [7] его же, там же, 1959, т. 124, № 1, с. 15 - 18; [8] Саrlеman Т., "С. r. Acad. sci", 1933, t. 197, p. 471; [9] Бицадзе А. В., Краевые задачи для эллиптических уравнений второго порядка, М., 1966; [10] Халилов 3. И., "Изв. АН СССР. Сер. матем.", 1947, т. 11, с. 345-62; [11] Courant R., Hilbert D., Methods of mathematical physics, v. 2, 2 ed., N.Y.-L., 1962.
И. Н. Benya.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; функциональные методы решения - методы, основанные на рассмотрении левой части уравнения как оператора, действующего в функциональном пространстве, определенном соответствующим образом. Наибольшее развитие функциональные методы получили в применении к линейным уравнениям с частными производными. В этом случае функциональные методы условно могут быть разбиты на две группы: а) относящиеся к спектральной теории дифференциальных операторов и б) используемые при выяснении общего характера разрешимости уравнений, краевых задач и свойств решений. Внутри группы б) удобно, в свою очередь, выделить, с одной стороны, методы, опирающиеся лишь на общие теоремы функционального анализа (теории операторов), а с другой - методы, существенно использующие технику преобразования Фурье. Для первых характерно непосредственное рассмотрение краевых задач для общих уравнений с переменными коэффициентами; для вторых отправной точкой является изучение дифференциального оператора с постоянными- коэффициентами, часто безотносительно к краевым условиям, а переход к переменным коэффициентам (когда это возможно) осуществляется при помощи соответствующей "теории возмущений". Получаемые в обоих направлениях результаты дополняют друг друга.
Функциональные методы возникли при использовании связи между задачей минимизации функционала
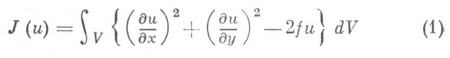
в классе действительных функций и( х, у), удовлетворяющих на границе Sобласти V(для простоты - двумерной) условию

и задачей решения уравнения Пуассона

в V[являющегося уравнением Эйлера для (1)] при тех же краевых условиях (2). Если f не является гладкой (напр.,
 - гильбертову пространству функций с суммируемым в Vквадратом), то минимум для
- гильбертову пространству функций с суммируемым в Vквадратом), то минимум для(1) достигается на функциях, не имеющих, вообще говоря, вторых производных, входящих в уравнение (3), т. е. эти функции дают лишь обобщенное решение задачи (3), (2). Для исчерпывающего описания возникающей ситуации (см. [1], [2]) вводится гильбертово пространство W1, получаемое пополнением линейного многообразия гладких функций, удовлетворяющих (2), внорме, порождаемой скалярным произведением

Тогда под решением задачи (3), (2) понимается элемент uО W1 такой, что для любого элемента uО W1 выполняется равенство
 (4)
(4)где круглые скобки означают скалярное произведение в H(V). Минимум для (1) при любой
 также достигается в W1 и дает решение задачи (3), (2) в смысле (4), являющееся единственным. Всякое классическое {имеющее вторые производные) решение задачи (3), (2) удовлетворяет равенству (4) при любой допустимой функции vи, значит, является обобщенным. Отсюда, в частности, следует определение, с помощью обобщенного решения, нек-рого расширения классич. оператора - D, заданного первоначально на гладких функциях, удовлетворяющих условию (2). Вопрос "при каких условиях на f и границу Sобобщенное решение будет классическим?" значительно более сложен (это - вопрос о так наз. дифференциальных свойствах обобщенного решения).
также достигается в W1 и дает решение задачи (3), (2) в смысле (4), являющееся единственным. Всякое классическое {имеющее вторые производные) решение задачи (3), (2) удовлетворяет равенству (4) при любой допустимой функции vи, значит, является обобщенным. Отсюда, в частности, следует определение, с помощью обобщенного решения, нек-рого расширения классич. оператора - D, заданного первоначально на гладких функциях, удовлетворяющих условию (2). Вопрос "при каких условиях на f и границу Sобобщенное решение будет классическим?" значительно более сложен (это - вопрос о так наз. дифференциальных свойствах обобщенного решения).В рассмотренной схеме существование обобщенного решения следовало из существования в
 элемента, реализующего минимум функционала (1). В дальнейшем было замечено, что теорема существования может быть получена непосредственно из определения (4) при помощи так наз. теоремы Рисса об общем виде линейного ограниченного функционала (см. [1]). Последующее развитие теории идет в нескольких направлениях. Приведенные построения немедленно обобщаются на случай, когда -D заменяется на общий самосопряженный положительный эллиптич. оператор порядка 2т с переменными коэффициентами. При этом, естественно, в скалярное произведение будут входить производные порядка т. Свойство полной непрерывности обратного оператора позволяет установить характер спектра соответствующих задач и установить справедливость для них Фредголъма альтернативы. Можно получить теорему существования решения и в - случае, когда в уравнении присутствует подчиненный главной эллиптич. части кососимметрич. оператор (напр., вместе с -D имеются-члены а( х, у)
элемента, реализующего минимум функционала (1). В дальнейшем было замечено, что теорема существования может быть получена непосредственно из определения (4) при помощи так наз. теоремы Рисса об общем виде линейного ограниченного функционала (см. [1]). Последующее развитие теории идет в нескольких направлениях. Приведенные построения немедленно обобщаются на случай, когда -D заменяется на общий самосопряженный положительный эллиптич. оператор порядка 2т с переменными коэффициентами. При этом, естественно, в скалярное произведение будут входить производные порядка т. Свойство полной непрерывности обратного оператора позволяет установить характер спектра соответствующих задач и установить справедливость для них Фредголъма альтернативы. Можно получить теорему существования решения и в - случае, когда в уравнении присутствует подчиненный главной эллиптич. части кососимметрич. оператор (напр., вместе с -D имеются-члены а( х, у) +b( х, у)
+b( х, у) ), т. е. и при отсутствии связи с вариационными задачами [3].
), т. е. и при отсутствии связи с вариационными задачами [3].Обобщения иного характера возникают из замечания о сохранении теоремы существования и единственности обобщенного решения задЧчи (3), (2) и в том случае, когда f - произвольный ограниченный линейный функционал над W1. Пространство всех таких функцию налов может быть получено пополнением Н по ново норме

Получаемое пространство
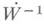 оказывается сущест венно шире Д. Напр., в одномерном случае (V- интервал (-1, 1)) последовательность функций
оказывается сущест венно шире Д. Напр., в одномерном случае (V- интервал (-1, 1)) последовательность функций
сходится в
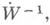 но расходится в II. Предел этой последовательности не является функцией в обычном смысле, т. е. пространство
но расходится в II. Предел этой последовательности не является функцией в обычном смысле, т. е. пространство  содержит обобщенным функции. В то же время неравенство
содержит обобщенным функции. В то же время неравенство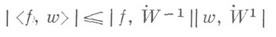
(скобки
 обозначают действие функционала f на элемент
обозначают действие функционала f на элемент  ) обеспечивает справедливость теоремы существования и единственности в случае
) обеспечивает справедливость теоремы существования и единственности в случае 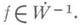 Этот результат интересен еще и в том отношении, что Teпeрь оператор - D устанавливает изоморфизм между пространствами
Этот результат интересен еще и в том отношении, что Teпeрь оператор - D устанавливает изоморфизм между пространствами  и
и  При
При 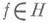 и гладкой Sобобщенное решение задачи (3), (2) не только принадлежит
и гладкой Sобобщенное решение задачи (3), (2) не только принадлежит  но всегда имеет и вторые обобщенные производные (
но всегда имеет и вторые обобщенные производные (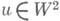 ), причем
), причем 
При n=2 (n - размерность V)пространство W-2 (функционалов над W2 )содержит d-функцию, т. е. функционал, определяемый равенством
 Существует принадлежащее пространству Нобобщенное решение уравнения
Существует принадлежащее пространству Нобобщенное решение уравнения  такое, что для u-обобщенного решения задачи (3), (2) верна формула
такое, что для u-обобщенного решения задачи (3), (2) верна формула
или

Это составляет абстрактную теорему существования функции Грина задачи (3), (2). Соответствующие построения осуществимы и в пространстве произвольного числа измерений для общих эллиптич. операторов [4]. Следующим (после эллиптич. операторов) объектом, к к-рому успешно были применены общие функциональные методы, явились уравнения с выделенным переменным - "временем", непосредственно обобщающие классические параболич. и гиперболич. уравнения математич физики. Здесь основные результаты условно могут быть разбиты на 3 группы: относящиеся к операторным уравнениям с 1-й и 2-й производной по времени [5], к симметричным положительным системам с частными производными 1-го порядка [3], [6] и к задаче Коши для гиперболич. уравнения произвольного порядка. Первая группа результатов излагается обычно либо в контексте обыкновенных дифференциальных уравнений в банаховом пространстве и теории полугрупп операторов, либо, вместе со второй и третьей группами, в рамках так наз. техники энергетич. нераренств. Последняя, в общих чертах, заключается в следующем. Для гладких решений уравнения со временем, записанного в операторной форме
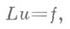 (6)
(6)подчиненных соответствующим начальным и краевым условиям, устанавливается неравенство вида

где Н 1, H2 - соответствующим образом определенные функциональные пространства. Для простоты их считают гильбертовыми. Напр., для
 удовлетворяющих в единичном квадрате Vуравнению
удовлетворяющих в единичном квадрате Vуравнению
и условиям

умножением на du/dt, интегрированием по Vи элементарными преобразованиями можно получить неравенство вида
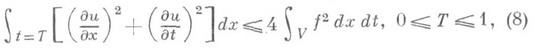
(являющееся математич. выражением нек-рого закона сохранения, откуда и термин "энергетическое неравенство"), соответствующее неравенству (7) при надлежащем определении норм в Н 1, Н 2. Определив обобщенное решение уравнения (6) как элемент иО Н х, для к-рого существует последовательность гладких функций и i, удовлетворяющих описанным краевым условиям, такая, что
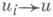 в H1 и
в H1 и  в H2, одновременно получают определение оператора L:
в H2, одновременно получают определение оператора L: (снова являющегося расширением классического), для к-рого существует ограниченный обратный оператор, что эквивалентно теореме единственности обобщенного решения. Следующим шагом исследования уравнения (6) является доказательство существования такого решения при любой допустимой правой части
(снова являющегося расширением классического), для к-рого существует ограниченный обратный оператор, что эквивалентно теореме единственности обобщенного решения. Следующим шагом исследования уравнения (6) является доказательство существования такого решения при любой допустимой правой части  Так как область изменения RL оператора Lявляется замкнутым подпространством в Н 2, доказательство единственности эквивалентно доказательству пустоты ортогонального дополнения к RL: из равенства
Так как область изменения RL оператора Lявляется замкнутым подпространством в Н 2, доказательство единственности эквивалентно доказательству пустоты ортогонального дополнения к RL: из равенства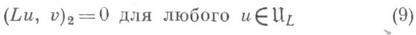
(скалярное произведение в Н 2). следует v=0. Равенство (9), с точки зрения теории операторов, означает, что
 и L*v=0, т. е. требуемый результат немедленно следовал бы из теоремы о единственности решения уравнения L*v=g. Однако доказательство такой теоремы требует специальных построений, часто весьма сложных, поскольку для L* (определенного с точки зрения классич. анализа с помощью нек-рого интегрального тождества) наличие неравенства, аналогичного (7) (так же, как и наличие для vпоследовательности сходящихся к ней гладких функций, удовлетворяющих нужным граничным условиям), отнюдь не очевидно. Возникающие трудности являются отражением несамосопряженности задач со "временем". При исследовании гиперболич. уравнений 2-го и высшего порядков использование (9) для доказательства равенства у=0 проводится обычно следующим образом: подбирается оператор Р* такой, что
и L*v=0, т. е. требуемый результат немедленно следовал бы из теоремы о единственности решения уравнения L*v=g. Однако доказательство такой теоремы требует специальных построений, часто весьма сложных, поскольку для L* (определенного с точки зрения классич. анализа с помощью нек-рого интегрального тождества) наличие неравенства, аналогичного (7) (так же, как и наличие для vпоследовательности сходящихся к ней гладких функций, удовлетворяющих нужным граничным условиям), отнюдь не очевидно. Возникающие трудности являются отражением несамосопряженности задач со "временем". При исследовании гиперболич. уравнений 2-го и высшего порядков использование (9) для доказательства равенства у=0 проводится обычно следующим образом: подбирается оператор Р* такой, что  и
и
Если заметить еще, что получение (7) основано обычно на рассмотрении выражения вида (Lu, Qu)2, где Q- оператор, подобранный так, что

и записать теперь (10) в виде

то можно считать, что исследование (6) основывается на этой паре неравенств (называемых иногда дуальным и). Сказанное относится главным образом к гиперболич. уравнениям. Параболич. уравнения допускают трактовку, более близкую к эллиптич" случаю. Преобразование Фурье позволяет провести, в известном смысле, исчерпывающее изучение задачи Коши для уравнений с постоянными коэффициентами [10]. Кроме того, преобразование Фурье, вместе с так наз. "замораживанием коэффициентов" (т. е. заменой оператора с переменными коэффициентами оператором с постоянными коэффициентами, равными значениям соответствующих коэффициентов в нек-рой фиксированной точке), часто используется для получения энергетич. неравенств при использовании схем рассмотренного выше типа, а также играет важную роль в локальной характеризации операторов и краевых условий при исследовании краевых задач для эллиптич. урав- . нений [10]. Дальнейшее развитие этих идей привело К введению и изучению псевдодифференциальных операторов. Кроме того, с помощью преобразования Фурье было установлено, что для дифференциальной операции Lс постоянными коэффициентами, рассматриваемой в компактной области Vевклидова пространства на функциях
 т. е. равных нулю на границе вместе со всеми производными, всегда имеет место неравенство
т. е. равных нулю на границе вместе со всеми производными, всегда имеет место неравенство
Взяв для Lзамыкание
 в И(V)(областью определения для Lсчитают
в И(V)(областью определения для Lсчитают  ) и определив Lкак сопряженный
) и определив Lкак сопряженныйк
 (в H(V)), получают, что RL=H(V). Наличие неравенства (11) для решений уравнения (6), обеспечивающее единственность решения, автоматически влечет и разрешимость при любой правой части уравнения L*v=g, содержащего сопряженный оператор. Используя теорему Банаха, можно заключить, что существует оператор
(в H(V)), получают, что RL=H(V). Наличие неравенства (11) для решений уравнения (6), обеспечивающее единственность решения, автоматически влечет и разрешимость при любой правой части уравнения L*v=g, содержащего сопряженный оператор. Используя теорему Банаха, можно заключить, что существует оператор  (т. е.
(т. е.  является расширением минимального оператора
является расширением минимального оператора  и сужением максимального
и сужением максимального  ), такой, что
), такой, что  причем существует ограниченный (в Н)обратный оператор
причем существует ограниченный (в Н)обратный оператор  (см. [10]). Можно считать, что
(см. [10]). Можно считать, что  соответствует нек-рой краевой задаче (определяется нек-рой системой условий, "сосредоточенной" на границе и находящейся "между" тождественно нулевыми условиями и полным отсутствием условий). О характере условий, определяющих оператор
соответствует нек-рой краевой задаче (определяется нек-рой системой условий, "сосредоточенной" на границе и находящейся "между" тождественно нулевыми условиями и полным отсутствием условий). О характере условий, определяющих оператор  в общем случае известно мало. Использование преобразования Фурье лежит также в основе исследования широкого круга вопросов теории дифференциальных операторов, связанных с изучением структуры фундаментального решения и так наз. локальных свойств решений уравнений (в отличие от исследования свойств решений краевых задач). Сюда относятся теорема о существовании фундаментального решения для общего оператора с постоянными коэффициентами, теорема о локальной (в окрестности данной точки) разрешимости уравнения с правой частью и о характере гладкости этого решения (см. [9], [11]). В связи с тем, что в случае переменных (комплексных) коэффициентов локальная разрешимость неоднородного уравнения (6) не всегда имеет место (для уравнения
в общем случае известно мало. Использование преобразования Фурье лежит также в основе исследования широкого круга вопросов теории дифференциальных операторов, связанных с изучением структуры фундаментального решения и так наз. локальных свойств решений уравнений (в отличие от исследования свойств решений краевых задач). Сюда относятся теорема о существовании фундаментального решения для общего оператора с постоянными коэффициентами, теорема о локальной (в окрестности данной точки) разрешимости уравнения с правой частью и о характере гладкости этого решения (см. [9], [11]). В связи с тем, что в случае переменных (комплексных) коэффициентов локальная разрешимость неоднородного уравнения (6) не всегда имеет место (для уравнения  имеется такая
имеется такая  что не существует решения, даже
что не существует решения, дажев классе обобщенных функций, ни в каком открытом непустом подмножестве R3, см. [9]), исследуются условия, обеспечивающие локальную разрешимость.
Использование функциональных методов весьма плодотворно и при изучении нелинейных, уравнений с частными производными. Это прежде всего относится к вариационным методам (если вместо функционала (1) рассматривать более общий, то связанное с ним уравнение Эйлера оказывается нелинейным) (см. [12]), различным вариантам метода неподвижной точки (см. Шаудера метод), к методу продолжения по параметру (см. [3], [13]), и другим, применяемым главным образом к эллиптич. и параболич. уравнениям. Метод энергетич. неравенств успешно используется при изучении квазилинейных гиперболич. уравнений.
Лит.:[1] Соболев С. Л., Некоторые применения функционального анализа в математической физике, Новосиб., 1962; [2] Курант Р., Гильберт Д., Методы математической физики, пер. с нем., 3 изд., т. 1-2, М.- Л., 1951; [3] Берс Л., Джон Ф., Шехтер М., Уравнения с частными производными, нер. с англ., М., 1966; [4] Liоns J., Equations differtntielles operationelles et problemes aux limites, В., 1961; [5] Xилле Э.,Филлипс Р., Функциональный анализ и полугруппы, пер. с англ., 2 изд., М., 1962; [6] Нагумо М., Лекции по современной теории дифференциальных уравнений в частных производных, пер. с япон., М.,1967; [7] Гординг Л., Задачи Коши для гиперболических уравнений, пер. с англ., М., 1961; [8J Гельфанд И. М., Шилов Г. Е., Некоторые вопросы теории дифференциальных уравнений, М., 1958; [9] Хёрмандер Л., Линейные дифференциальные операторы с частными производными, пер. с англ., М., 1965; [10] его же, К теории общих дифференциальных операторов в частных производных, пер. с англ., М., 1959; [11] Трев Ж., Лекции по линейным уравнениям в частных производных с постоянными коэффициентами, пер. с англ., М., 1965; [12] Ладышенекая О. А., Уральцева Н. Н., Линейные и квазилинейные уравнения эллиптического типа, М., 1964; [13] Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., М., 1957
А. А. Дезин.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
