- ИНДУКТИВНЫЙ ПРЕДЕЛ
- конструкция, к-рая впервые появилась в теории множеств, а затем стала широко использоваться в алгебре, топологии и других областях математики. Важный частный случай И. п.- это И. п. направленного семейства однотипных математических структур. Пусть С- направленное по возрастанию предупорядоченное множество, т. е. в Сзадано рефлексивное и транзитивное отношение
 и для любых элементов a,
и для любых элементов a,  найдется такой элемент
найдется такой элемент  что
что 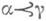 и
и 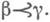 И пусть каждому
И пусть каждому  сопоставлена некоторая структура А a. (для определенности можно считать, что А a.- группы) и при
сопоставлена некоторая структура А a. (для определенности можно считать, что А a.- группы) и при  заданы гомоморфизмы jab :
заданы гомоморфизмы jab : удовлетворяющие двум условиям:
удовлетворяющие двум условиям: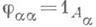 для любого и
для любого и 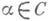
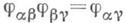 для любых
для любых  из С. На множестве
из С. На множестве  вводится отношение эквивалентности
вводится отношение эквивалентности 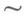 : элемент
: элемент 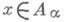 эквивалентен элементу
эквивалентен элементу 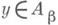 , если xjag=yjbg. для некоторого у. Фактормножество
, если xjag=yjbg. для некоторого у. Фактормножество 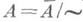 можно снабдить структурой группы: если
можно снабдить структурой группы: если 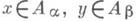 и
и 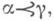
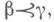 то произведением классов эквивалентности с представителями хи усчитается класс эквивалентности с представителем
то произведением классов эквивалентности с представителями хи усчитается класс эквивалентности с представителем 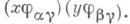 Построенная группа Аназ. И. п. семейства групп А a. Для каждого
Построенная группа Аназ. И. п. семейства групп А a. Для каждого 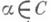 существует естественный гомоморфизм ja :
существует естественный гомоморфизм ja :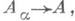 который элементу
который элементу  сопоставляет его класс эквивалентности. Группа А, вместе с гомоморфизмами ja, обладает следующим универсальным свойством: для любой системы гомоморфизмов ya :
сопоставляет его класс эквивалентности. Группа А, вместе с гомоморфизмами ja, обладает следующим универсальным свойством: для любой системы гомоморфизмов ya :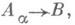
 для которой
для которой 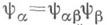 при
при 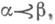 существует такой единственный гомоморфизм y :
существует такой единственный гомоморфизм y :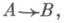 что
что 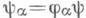 для любого
для любого 
Обобщением данной конструкции И. п. является индуктивный предел (прямой предел, копредел) функтора. Объект Акатегории
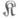 наз. индуктивным пределом ковариантного функтора F:
наз. индуктивным пределом ковариантного функтора F: если:
если:1. существуют такие морфизмы jD :
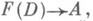 где
где  что
что 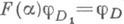 для любого морфизма а :
для любого морфизма а : 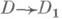 из
из 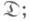
2. для любого семейства морфизмов yD :
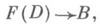 где
где  для к-рого
для к-рого 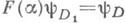 при любом a.: D
при любом a.: D D1 из
D1 из 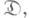 существует такой единственный морфизм у:
существует такой единственный морфизм у: что
что 
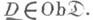
И. п. обозначается
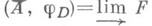 или
или 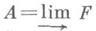 или
или  И. п. контравариантного функтора
И. п. контравариантного функтораF:
 определяется как индуктивный предел ковариантного функтора F* из двойственной к
определяется как индуктивный предел ковариантного функтора F* из двойственной к 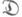 категории D* в категорию
категории D* в категорию 
Всякое предупорядоченное множество С можно рассматривать как категорию, объектами к-рой являются элементы множества С, а морфпзмами - всевозможные пары (a, b), где а,
 ис
ис 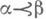 очевидным законом композиции. В произвольной категории Псемейство объектов А a,
очевидным законом композиции. В произвольной категории Псемейство объектов А a,  . и морфпзмов jab :
. и морфпзмов jab :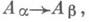 где
где 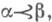 можно рассматривать как образ функтора
можно рассматривать как образ функтораF:
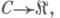 если
если  и при
и при 
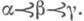
Если
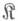 - категория множеств (групп, топологич. пространств и т. п.), то И. п. функтора F:С->p совпадает с приведенной выше конструкцией индуктивного предела.
- категория множеств (групп, топологич. пространств и т. п.), то И. п. функтора F:С->p совпадает с приведенной выше конструкцией индуктивного предела.Если
 - малая дискретная категория, то И. п. любого функтора Fиз
- малая дискретная категория, то И. п. любого функтора Fиз 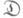 в произвольную категорию
в произвольную категорию 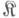 есть копроизведение объектов F(D),
есть копроизведение объектов F(D),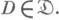 В частности, если категория
В частности, если категория  пуста, то И. п. есть левый нуль, или инициальный объект категории
пуста, то И. п. есть левый нуль, или инициальный объект категории 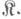 Коядра пар морфизмов любой категории
Коядра пар морфизмов любой категории  являются И. п. функторов со значениями в
являются И. п. функторов со значениями в 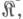 к-рые определены на категории с двумя объектами X и Y и четырьмя морфизмами 1X, 1Y и a, b:
к-рые определены на категории с двумя объектами X и Y и четырьмя морфизмами 1X, 1Y и a, b: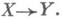
Всякий ковариантный функтор Fиз произвольной малой категории
 в категорию
в категорию  обладает И. п. тогда и только тогда, когда
обладает И. п. тогда и только тогда, когда  - категория с копроизведениями и коядрами пар морфизмов.
- категория с копроизведениями и коядрами пар морфизмов.Лит.:[1] Александров П. С, Топологические теоремы двойственности, ч. 1, М., 1955 (Тр. Матем. ин-та АН СССР, т. 48); [2] Бунур И., Деляну А., Введение в теорию категорий и функторов, пер. с англ., М., 1972; [2] Цаленко М. Ш., Шульгейфер Е. Г., Основы теории категорий, М., 1974.
М. Ш. Цаленко.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
