АНАЛИТИЧЕСКАЯ ФУНКЦИЯ

функция, к-рая может быть представлена степенным рядом. Исключит, важность класса А. ф. определяется следующим. Во-первых, этот класс достаточно ш и р о к: он охватывает большинство функций, встречающихся в основных вопросах математики и ее приложений к естествознанию и технике. Во-вторых, класс А. ф. з амкнут относительно основных операций арифметики, алгебры и анализа. Наконец, А. ф. обладают важным свойством единственности: каждая А. ф. образует одно "органически связанное целое", представляет собой "единую" функцию во всей своей естественной области существования. Это свойство, к-рое в 18 в. считалось неотделимым от самого понятия функции, приобрело принципиальное значение после установления - в 1-й пол. 19 в.- общей точки зрения на функцию как на произвольное соответствие. Теория А. ф. была создана в 19 в. в первую очередь благодаря работам О. Коши (A. Cauchy), Б. Римана (В. Riemann) и К. Вейерштрасса (К. Weierstrass). Решающее значение в построении этой теории сыграл "выход в комплексную область". Теория А. ф. возникла как теория функций комплексного переменного; и в настоящее время (70-е гг. 20 в.) теория А. ф. составляет основное содержание общей теории функций комплексного переменного.

Существуют различные подходы к понятию аналитичности. В основе одного из них, впервые развитого О. Коши и далеко продвинутого Б. Риманом, лежит структурное свойство функции - существование производной по комплексному неременному, или комплексная дифференцируемость. Этот подход тесно связан с геометрическими представлениями. Другой подход, систематич. развивавшийся К. Вейерштрассом, основывается на возможности представления функций степенными рядами; он связан, тем самым, с аналитическим аппаратом, к-рым может быть изображена функция. Основной факт теории А. ф. заключается в тождественности соответствующих классов функций, рассматриваемых в произвольной области комплексной плоскости.

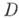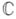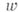Перейдем к точным определениям. Пусть - область в комплексной плоскости . Если каждой точке поставлено в соответствие нек-рое комплексное число , то говорят, что в области 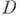определена (однозначная) функция f комплексного переменного 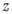, и пишут: 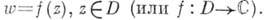Функция 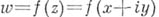может рассматриваться как комплексная функция двух действительных переменных хи у, определенная в области ( 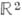- евклидова плоскость). Задание такой функции равносильно заданию двух действительных функций

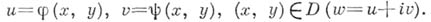
Зафиксировав точку 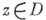, придадим 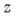приращение 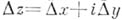(так, что 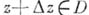) и рассмотрим соответствующее приращение функции :

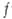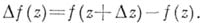
Если

при 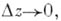или, что то же, если существует

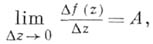
то функция 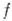наз. дифференцируемой (в смысле комплексного анализа, или в смысле 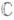) в точке 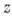; 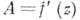- 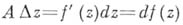производная функция 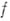в точке 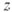, а - ее дифференциал в этой точке. Функция 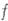, дифференцируемая в каждой точке области D, наз. дифференцируемой в области D.

Сравним понятия дифференцируемости функции 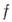как функции двух действительных переменных (в смысле 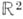) н в смысле 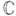. В первом случае дифференциал 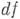имеет вид

где

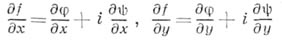
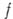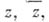- частные производные функции . Переходя от независимых переменных к переменным к-рые формально можно считать новыми независимыми переменными, связанными со старыми соотношениями 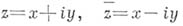(становясь на эту точку зрения, функцию 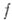иногда записывают в виде ), и, выражая 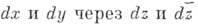по обычным правилам вычисления

дифференциалов, получают запись 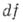в комплексной форме:

где

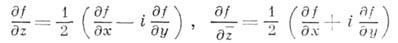
- (формальные) производные функции 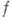по и 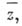соответственно. Отсюда видно, что дифференцируемость функции в смысле С имеет место в том и только том случае, когда она дифференцируема в смысле 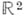и справедливо равенство , к-рое в развернутой форме можно переписать так:

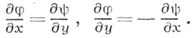
Если функция f дифференцируема в смысле 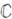в области D, то последние соотношения справедливы в каждой точке этой области; они наз. уравнениями Коши- Римана. Эти уравнения встречались уже в 18 в. в связи с изучением функций комплексного переменного в трудах Ж. Л. Д'Аламбера и Л. Эйлера (J. L. D'Alembert, L. Euler). Определение, данное в начале, уточняется так. Функция f, определенная в области D, наз. голоморфной (аналитической) вточке , если существует окрестность этой точки, в к-рой функция f представляется степенным рядом

Если это свойство имеет место в каждой точке 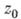области 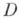, то функция 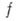наз. голоморфной (аналитической) в области .

Функция , голоморфная в точке 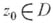, дифференцируема в этой точке. Более того, сумма сходящегося степенного ряда имеет производные всех порядков (бесконечно дифференцируема)

по комплексному переменному 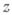; коэффициенты ряда могут быть выражены через производные функции 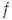в точке 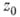по формулам

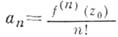. Степенной ряд, записанный в форме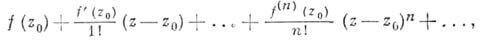

наз. рядом Тейлора функции 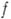в точке 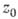. Тем самым, голоморфность функции в области 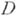означает, что в каждой точке области 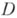функция 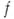бесконечно дифференцируема и ее ряд Тейлора сходится к ней в нек-рой окрестности этой точки.

С другой стороны, в теории А. ф. устанавливается следующий замечательный факт: функция 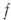, дифференцируемая в области , голоморфна в этой области (в отдельной точке это утверждение неверно: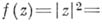 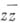дифференцируема в точке 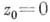, но нигде не голоморфна). Следовательно, понятия комплексной диф-ференцируемости и голоморфности функции в области тождественны; каждое из следующих свойств функции 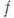в области - дпфференцируемость в смысле 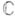, дифференцируемость в смысле вместе с вы. полнением уравнений Коши - Рпмана, голоморфность - может служить определением аналитичности f в этой области.

Еще одна характеристика А. ф. связана с понятием интеграла. Интеграл от функции 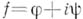вдоль (ориентированной спрямляемой)кривой Г: 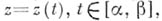может быть определен формулой:

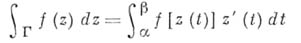
или при помощи криволинейного интеграла:

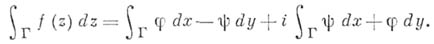
Центральное место в теории А. ф. занимает следующая интегральная теорема Коши: если 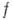- А. ф. в области D, то 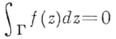для любой замкнутой кривой 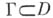, ограничивающей область, принадлежащую D. Верио и обратное заключение (теорема Морер ы): если f непрерывна в области D и 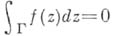для любой такой кривой Г, то 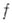- А. ф. в области D. В частности, в односвязной области аналитическими являются те п только те непрерывные функции f, для к-рых интеграл по любой замкнутой кривой равен нулю (или, что то же самое, интеграл по любой кривой Г, соединяющей произвольные точки 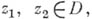зависит только от точек 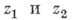и не зависит от формы этой кривой). Эта характеристика А. ф. лежит в основе многих их приложений. Интегральная теорема Коши позволяет получить интегральную фор мулу Коши, выражающую значения А. ф. внутри области через ее значения на границе этой области:

здесь D - область, граница к-рой 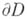состоит из конечного числа непересекающихся спрямляемых кривых (ориентация 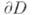предполагается положительной относительно области D), f - функция, аналитическая в нек-рой области 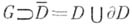. Эта формула позволяет, в частности, свести изучение многих вопросов, связанных с А. ф., к соответствующим вопросам для простейшей функции - ядра Коши 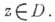(Подробнее см. статью Интегральные представления аналитических функций.)

Важнейшее свойство А. ф. выражается следующей теоремой единственности: две функции, аналитические в области Dи совпадающие на к.-л. множестве, имеющем предельную точку в D, совпадают и во всей области D(тождественны). В частности, А. ф. отличная от тождественного нуля, может иметь в области Dлишь изолированные нули. Если при этом 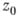- нуль функции 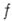, то в некоторой окрестности точки 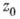имеем 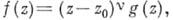где 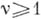- натуральное число (называемое кратностью нуля функции 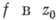), а 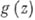- А. ф. в 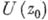, отличная от нуля.

Важную роль в изучении А. ф. играют точки, в к-рых нарушается свойство аналитичности - так наз. особые точки А. ф. Рассмотрим здесь изолированные особые точки (однозначных) А. ф. (подробнее см. Особая точка аналитической функции). Если f - А. ф. в кольце вида 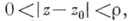то она разлагается в этой области вряд Лорана

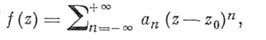
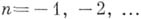содержащий, вообще говоря, не только положительные, но и отрицательные степени . Если в этом разложении члены с отрицательными степенями отсутствуют ( для ), то 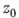наз. правильной точкой f (устранимой особой точкой). В правильной точке существует и конечен

полагая 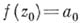, получаем А. ф. во всем круге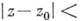 . Если ряд Лорана функции содержит лишь конечное число членов с отрицательными степенями z- z₀:

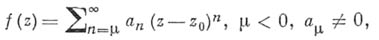
то точка 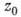наз. полюсом функции 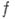(кратности ); полюс 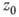характеризуется тем, что

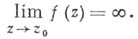
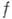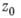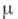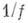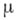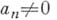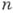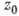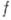Функция имеет в точке полюс кратности тогда и только тогда, когда функция имеет в этой точке нуль кратности . В случае, когда ряд Лорана содержит бесконечное число отрицательных степеней ( для бесконечного множества отрицательных индексов ), точка наз. существенно особой точкой; в таких точках не существует ни конечного, ни бесконечного предела функции . Коэффициент разложения функции в ряд Лорана с центром в изолированной особой точке 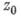наз. вычетом функции 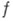в точке :

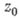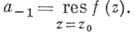
Вычет функции 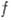в точке 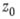может быть определен формулой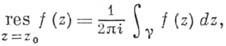

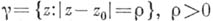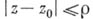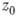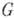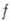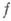где - достаточно мало (так что круг не содержит особых точек функции f, отличных от ). Важная роль вычетов определяется следующей теоремой: если - А. ф. в области , за исключением нек-рого множества изолированных особых точек, - контур, ограничивающий область и не проходящий через особые точки функции , - все особые точки , лежащие в 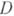, то

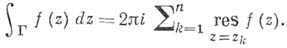
Эта теорема дает эффективное средство для нахождения интегралов (см. также Вычет).

Сумма членов ряда Лорана функции 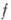в точке 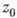, соответствующая отрицательным индексам ,

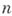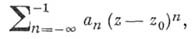
наз. главной частью ряда Лорана (или функции f) в точке 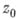. Именно главная часть определяет характер особенности функции 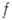в точке .

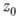Функции, представимые в виде отношения двух функций, голоморфных в области D, наз. мероморф-ными в области Д. Мероморфная в области функция голоморфна в этой области за исключением, быть может, конечного или счетного множества полюсов; в полюсах значения мероморфной функции считаются равными бесконечности. Если допустить такие значения, то мероморфные в области Dфункции могут быть определены как функции, к-рые в окрестности каждой точки представимы рядом по степеням 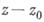, содержащим конечное (зависящее от ) число членов с отрицательными степенями .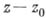

Часто аналитическими в области Dназ. как голоморфные, так и мероморфные в этой области функции. В этом случае голоморфные функции наз. также регулярными аналитическими, или просто регулярными.

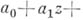
Простейший класс А. ф. составляют функции, голоморфные во всей плоскости; такие функции наз. ц ел ы м и. Целые функции представимы рядами 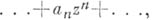сходящимися во всей плоскости. К ним относятся многочлены от 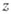, функции

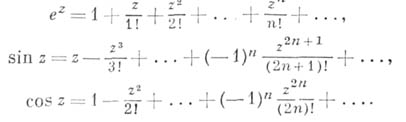
Теорема Вейерштрасса утверждает, что какова бы ни была последовательность комплексных чисел 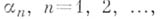не имеющая предельных точек в 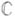, существует целая функция 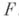, обращающаяся в нуль в точках 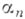, и только в этих точках (среди точек 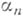могут быть совпадающие; им отвечает нуль функции Fсоответствующей кратности). При этом функция 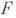может быть представлена в виде (вообще говоря, бесконечного) произведения целых функций, каждая из к-рых имеет только по одному нулю. Напр.,

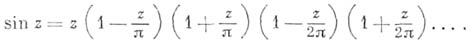
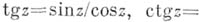
Функции, мероморфные во всей плоскости (т. е. представимые в виде отношения целых функций), наз. мероморфными функциями. Таковыми являются рациональные функции, 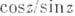, эллиптич. функции и др.

Согласно теореме Миттаг-Леффлера, для любой последовательности 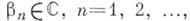не имеющей предельных точек в , существует мероморфная функция 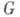с полюсами в точках 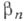(и только в этих точках), главные части к-рой в точках 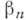совпадают ¹ с заранее заданными многочленами от . При этом функция G может быть представлена в виде (вообще говоря, бесконечной) суммы мероморфных функций, каждая из к-рых имеет полюс только в одной точке. Напр.,

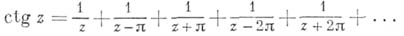
Теоремы о существовании голоморфной функции с заданными нулями и мероморфных функций с заданными полюсами и главными частями справедливы и для произвольной области .

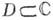Важное значение для изучения А. ф. имеют связанные с ними геометрич. представления. Если f : - А. ф., то образ f(D) области Dтакже является областью (принцип сохранения области). При 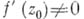отображение 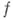сохраняет углы в 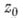как по величине, так и по знаку, т. е. является конформным. Таким образом, существует тесная связь между аналитичностью и важным геометрич. понятием конформного отображения. Если f - А. ф. в D ц 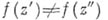при 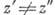(такие функции наз. однолистными), то 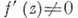в Dи f определяет взаимно однозначное и конформное отображение области Dна область 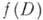. Теорема Римана, основная теорема теории конформных отображений, утверждает, что в любой односвязной области, граница к-рой содержит более одной точки, существуют однолистные А. ф., конформно отображающие эту область на круг или полуплоскость (см. Конформное отображение. Однолистная функция).

Действительная и мнимая части функции 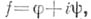голоморфной в области D, удовлетворяют в этой области уравнению Лапласа:

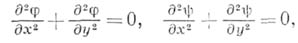
т. е. являются гармоническими функциями. Две гар-монпч. функции, связанные между собой уравнениями Коши - Рпмана, наз. сопряженными. В односвязной области любая гармонич. функция имеет сопряженную функцию 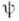и является, тем самым, действительной частью нек-рой голоморфной в Dфункции f.

Связи с конформными отображениями п гармонич. функциями лежат в основе многих приложений теории А. ф.

Функция 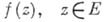( - произвольное множество) наз. аналитической в точке 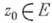, если существует окрестность этой точки, на пересечении к-рой с множеством 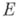функция 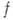представляется сходящимся степенным рядом. Функция 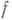наз. аналитической на множестве Е, если она ана-литнчна на нек-ром открытом множестве, содержащем Е(точнее, если существуют открытое множество, содержащее Е, и аналитическая на нем функция F, совпадающая с 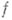на множестве ). Для открытых множеств понятие аналитичности совпадает с понятием дифференцируемости по множеству. Однако в общем случае это не так; в частности, на действительной прямой существуют функции, не только имеющие производную, но и бесконечно дифференцируемые в каждой точке, к-рые не являются аналитическими ни в одной точке этой прямой. Для справедливости теоремы единственности А. ф. существенно свойство связности множества Е. Именно поэтому А. ф. рассматриваются обычно в областях, т. е. на открытых и связных множествах.

Все сказанное выше относилось к однозначным А. ф. f, рассматриваемым в данной области D(пли на данном множестве Е).комплексной плоскости. Задаваясь вопросом о возможности продолжения функции f - как А. ф.- в большую область, приходят к понятию А. ф., рассматриваемой в целом - во всей своей естественной области существования. При таком продолжении данной функции область ее аналитичности, расширяясь, может налегать сама на себя, доставляя новые значения функции в точках плоскости, где она уже была определена. Поэтому А. ф., рассматриваемая в целом, вообще говоря, оказывается многозначной.

К необходимости изучения многозначных А. ф. приводят многие вопросы анализа (обращение функций, нахождение первообразных и построение А. ф. с заданной действительной частью в многосвязных областях, решение алгебраич. уравнений с аналитич. оэффициентами и др.); такими функциями являются алгебраические функции и т. д.

Регулярный процесс, приводящий к полной А. ф., рассматриваемой в своей естественной области существования, был указан К. Вейерштрассом; он носит назв. аналитического продолжения по Вейерштрассу.

Исходным является понятие элемента А. ф. - степенного ряда с ненулевым радиусом сходимости. Такой элемент :

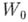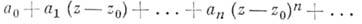
определяет нек-рую А. ф. f в своем круге сходимости К ₀. Пусть 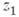- точка круга 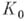, отличная от 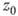. Разлагая функцию 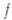в ряд с центром в точке 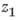, получаем новый элемент :

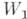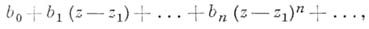
круг сходимости к-рого обозначим через 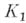. В общей части кругов 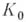и ряд сходится к той же функции, что и ряд 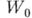. Если круг 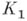выходит за пределы круга 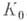, то ряд 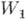определяет функцию, заданную посредством 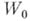, на нек-ром множестве вне 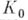(где ряд 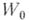расходится). В этом случае элемент 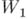наз. непосредственным аналитич. родолжением элемента 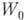. Пусть 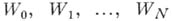- цепочка элементов, в к-рой 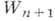является непосредственным аналитич. родолжением 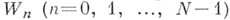; тогда элемент 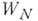наз. аналитич. родолжением элемента (посредством данной цепочки элементов). Может оказаться так, что центр круга 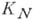принадлежит кругу 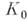, но элемент 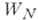не является непосредственным аналитич. родолжением элемента . В этом случае суммы рядов 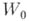и 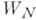в общей части кругов 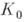и 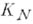имеют различные значения; тем самым аналитич. родолжение может привести к новым значениям функции в круге .

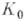Совокупность всех элементов, к-рые могут быть получены аналитич. родолжением элемента 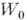, образуют полную А. ф. (в смысле Веперштрасса), порожденную элементом 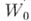; объединение их кругов сходимости представляет собой (вейерштрассову) о б-ласть существования этой функции. Из теоремы единственности А. ф. следует, что А. ф. в смысле Вейерштрасса полностью определяется заданием элемента 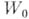. При этом в качестве исходного может быть взят любой другой элемент, принадлежащий этой функции; полная А. ф. от этого не изменится.

Полная А. ф.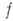, рассматриваемая как функция точек плоскости, принадлежащих ее области существования D, вообще говоря, является многозначной. Чтобы избавиться от многозначности, функцию рассматривают не как функцию точек плоской области D, а как функцию точек нек-рой (лежащей над областью D).многолпстной поверхности Rтакой, что каждой точке области Dсоответствует столько (проектирующихся в нее) точек поверхности Л, сколько различных элементов с центром в этой точке имеет полная А. ф. 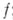; на поверхности Л функция 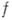становится однозначной функцией. Идея перехода к таким поверхностям принадлежит Б. Риману, а сами они носят назв. римановых поверхностей. Абстрактное определение понятия римановой поверхности позволило заменить теорию многозначных А. ф. теорией однозначных А. ф. на римановых поверхностях.

Фиксируем область 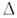, принадлежащую области существования 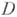полной А. ф. 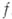, и к.-л. элемент Wфункции 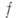с центром в точке области 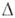. Совокупность всех элементов, к-рые могут быть получены аналитич. родолжением элемента 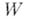посредством цепочек с центрами, принадлежащими А, наз. ветвью А. ф. f. Ветвь многозначной А. ф. может оказаться однозначной А. ф. в области А. Так, напр., произвольные ветви функци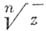й и 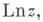соответствующие любой односвяз-ной области, не содержащей точку 0, являются однозначными функциями; при этом имеет ровно , а 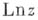- бесконечное множество различных ветвей в каждой такой области. Выделение однозначных ветвей (при помощи тех или иных разрезов области существования) и их изучение средствами теории однозначных А. ф. является одним из осп. приемов исследования конкретных многозначных А. ф. ^А- ^А- Гончар.

Аналитические функции нескольких комплексных переменных. Комплексное пространство 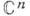(состоящее из точек 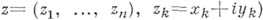- это векторное пространство над полем комплексных чисел с евклидовой метрикой

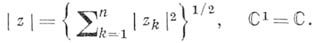
От 2n-мерного евклидова пространства 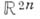оно отличается нек-рой асимметрией: при переходе от 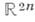к 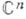(т. е. при введении в R²ⁿ комплексной структуры) координаты разбиваются на пары, к-рые выступают в комплексе .

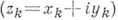Если комплексная функция 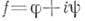задана в области и дифференцируема в каждой точке 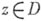в смысле 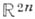(т. е. как функция 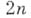действительных переменных 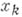и 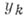), то ее дифференциал может быть представлен в виде

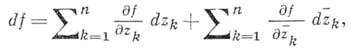
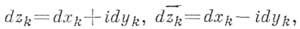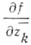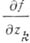где а символы и определяются так же, как и в плоском случае. <Если при этом 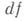имеет вид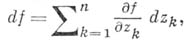

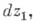
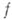т. е. является комплексно линейной функцией от то функция наз. дифференцируемой в смысле 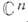, или голоморфной, или аналитической в области .

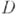Таким образом, условие голоморфности 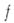в области состоит из условия ее дифференцируемости в смысле и системы пкомплексных равенств 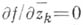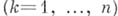, к-рая равносильна системе уравнений с частными производными 1-го порядка

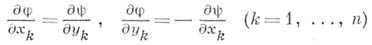
(системаКоши- Римана).

В пространственном случае 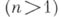, в отличие от плоского 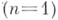, эта система переопределена - число уравнений превышает число неизвестных функций. Переопределенность остается и при переходе к геометрически более естественному пространственному аналогу голоморфной функции одного комплексного переменного - голоморфному отображению 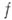, осуществляемому системой 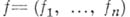из пголоморфных в области функций 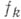. Отображение 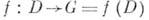наз. биголоморфным, если оно взаимно однозначно и голоморфно вместе с обратным 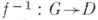. Условия голоморфности отображения 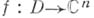выражаются системой 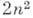действительных уравнений относительно действительных функций. Переопределенность условий голоморфности при является причиной ряда эффектов, специфичных для пространственного случая, таких, как отсутствие пространственного аналога Римана теоремы о существовании конформных отображений. По теореме Римана, при 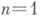всякие две односвязные области, границы которых не сводятся к точке, изоморфны. Однако при n> 1 неизоморфными оказываются даже такие простые односвязные области, как шар и произведение кругов (поликруг)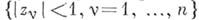 Неизоморфность обнаруживается при сравнении групп автоморфизмов этих областей (т. е. их биголоморфных отображений на себя) - группы оказываются алгебраически неизоморфными, а биголоморфное отображение одной области на другую, если бы оно существовало, устанавливало бы изоморфизм этих групп. Отмеченное обстоятельство существенно отличает теорию бпголоморфных отображений областей комплексного пространства от теории конформных отображений плоских областей.

Функция наз. голоморфной в точке 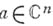, если она голоморфна в нек-рой окрестности этой точки. По условиям Коши - Римана, голоморфная в точке афункция нескольких переменных голоморфна по каждому переменному (при фиксированных значениях остальных переменных). Справедливо п обратное: если функция 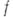в окрестности нек-рой точки голоморфна по каждому переменному в отдельности, то она голоморфна в этой точке (основная теорема Гартогса).

Голоморфность функции 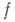в точке по аналогии с плоским случаем, эквивалентна ее разложимости в окрестности этой точки в кратный степенной ряд

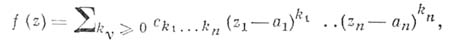
или, в сокращенной записи,

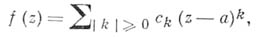
где 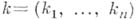- целочисленный векторный индекс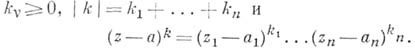

Голоморфная функция бесконечно дифференцируема, и этот ряд - ее ряд Тейлора, т. е.

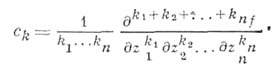
(производные берутся в точке а).

На голоморфные функции нескольких переменных распространяются основные факты теории голоморфных функций одного переменного, иногда в измененной формулировке, напр., Вейерштрасса теорема подготовительная, к-рая распространяет на пространственный случай свойство голоморфных функций одного переменного обращаться в нуль как целая степень . Теорема формулируется так: если голоморфная в точке 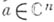функция 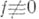равна нулю в этой точке, то в нек-рой окрестности ее можно представить (возможно, после невырожденного линейного преобразования независимых переменных) в виде

.

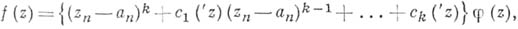где - целое число, 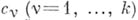- функции от , голоморфные в окрестности точки (штрих перед буквой обозначает проекцию в пространство первых 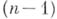координат) и равные нулю в а, а голоморфна и отлична от нуля в .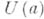

Эта теорема имеет принципиальное значение для изучения аналитических множеств, к-рые локально, в окрестности каждой своей точки, описываются как множества общих нулей иек-рого числа голоморфных в этой точке функций. Согласно теореме Вейерштрасса, такие множества локально описываются как множества общих нулей полиномов по одному переменному 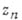с коэффициентами из кольца голоморфных функций от остальных переменных 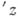. Это обстоятельство позволяет при локальном изучении аналнтич. множеств широко ..пользоваться алгебраич. методами.

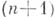Интегральная теорема Коши также несколько видоизменяется в пространственном случае и наз. теоремой Коши - Пуанкаре: пусть функция f голоморфна в области , тогда для любой мерной поверхности , компактно принадлежащей D, с кусочно гладкой границей

При этом интеграл, как и в плоском случае, определяется параметрич. заданием множества: если 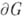имеет уравнение 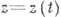, где параметр 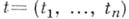меняется в тг-мерной клетке , то, по определению

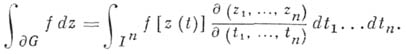
Отличие пространственного случая от плоского состоит в том, что здесь размерность поверхности Gменьше размерности области О, а в плоском случае эти размерности совпадают .

Пространственный аналог интегральной формулы Коши особенно просто выписывается для поликруговых областей, т. е. произведений плоских областей. Пусть - такая область, где - область плоскости комплексного переменного с кусочно гладкой границей 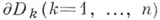, а функция f голоморфна в области, компактно содержащей D. Тогда последовательное применение интегральной формулы Коши для одного переменного дает для любой точки

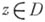
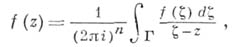
где 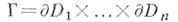есть n-мерная поверхность на границе 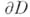, 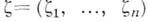и

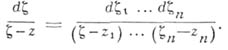
Однако поликруговые области составляют лишь весьма специальный класс, а в областях общего вида подобное разделение переменных невозможно. Роль интеграла Коши для произвольных областей 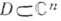с кусочно гладкой границей играет интегральная формула Мартинелли - Бохнер а: для любой функции 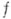, голоморфной в области, к-рая содержит 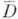, и для любой точки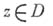

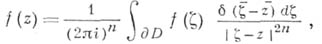
где 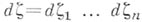, а

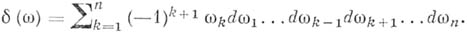
Это - формула Грина для пары функций, одна из к-рых голоморфна в D, а другая является фундаментальным решением уравнения Лапласа в пространстве 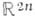с особенностью в точке 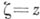. При это обычный интеграл Коши. При 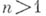формула отличается от кратного интеграла Коши для произведения плоских областей тем, что: во-первых, интегрирование в ней ведется по ( )-мерной границе области, а не по ее re-мерной части; во-вторых, ее ядро (множитель при 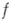под знаком интеграла) зависит от параметра 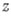не аналитически. В ряде задач, однако, аналитичность ядра существенна, и поэтому желательно построить интегральную формулу с таким ядром для возможно более широкого класса областей.

Обширный запас интегральных формул, в том числе для многих областей с аналитич. ядром, содержится в общей Лере формуле. Эта формула имеет вид

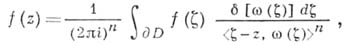
где 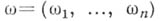- гладкая вектор-функция, 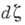и определены выше и 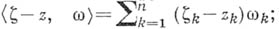предполагается, что 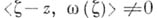при любом фиксированном 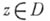и , пробегающем dD. Величина интеграла в этой формуле не зависит от выбора вектор-функции 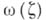(если только 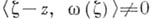при всех 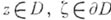), а при 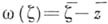этот интеграл совпадает с интегралом Мартинелли - Бохнера. Варьирование выбора со для разных классов областей позволяет получить из формулы Лере различные интегральные формулы. В теории А. ф. нескольких переменных рассматриваются и другие интегральные представления, справедливые для тех или иных классов областей. Важный класс составляют так наз. области Вейля, являющиеся обобщением произведения плоских областей. Для них справедливо Бергмана - Вейля представление с ядром, также аналитически зависящим от параметра.

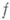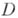Как и в плоском случае, основной интерес представляет изучение особенностей А. ф.; при этом принципиальное отличие пространственного случая от плоского выражается теоремой Осгуда - Брауна о стирании компактных особенностей, согласно к-рой любая функция , голоморфная в , где - область из 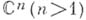, а К - компактно принадлежащее Dмножество, не разбивающее D, голоморфно продолжается во всю область D. По этой теореме голоморфные функции нескольких переменных не могут иметь изолированных особых точек. Место последних в 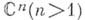занимают особые множества, к-рые являются аналитическими, если их размерность ниже 2п-1.

Отмеченное обстоятельство является определяющим для многомерной теории вычетов. В этой теории изучается задача о вычислении интеграла от функции f, голоморфной всюду в области 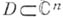, за исключением аналитич. множества М, по замкнутой n-мерной поверхности 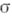, не пересекающейся с М. Так как размерность особого множества Мниже размерности Dпо крайней мере на 2, то Мне разбивает D. Если поверхность а не зацеплена с М, т. е. ограничивает 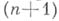мерную поверхность G, компактно принадлежащую 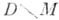, то (по теореме Коши - Пуанкаре). В общем случае для вычисления этого интеграла 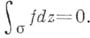нужно выяснить, как а зацеплена с особым множеством М, и вычислить интегралы по специальным n-мерным поверхностям, ассоциированным с отдельными порциями множества М(вычеты).

Решение этой задачи связано со значительными топологич. и аналитич. трудностями. В ряде случаев их помогают преодолеть методы, предложенные Мартинелли и Лере. Метод Мартинелли основан на применении топологич. принципа двойственности Александера - Понтрягина и сводит изучение n-мерных гомологии множества 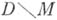к изучению -мерных гомологии особого множества М. Метод Лере имеет более общий характер; он основан на рассмотрении специальных гомологич. классов и вычислении нек-рых дифференциальных форм (форм-вычетов). Многомерная теория вычетов нашла приложения в теоретич. физике (см. Фейнмана интеграл).

Теорема Осгуда - Брауна выявляет важное принципиальное отличие пространственной теории от плоской. На плоскости для любой области Dможно построить функцию f, к-рая голоморфна в D и не продолжается аналитически за ее пределы, т. е. является естественной областью существования. В пространстве это не так: напр., шаровой слой не может быть областью существования никакой голоморфной функции, ибо по теореме Осгуда - Брауна любая голоморфная в нем функция непременно аналитически продолжается на весь шар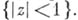

Возникает задача характеризации естественных областей существования голоморфных функций - так наз. областей голоморфности. Простой достаточный признак можно сформулировать при помощи понятия барьера в граничной точке области, т. е. функции 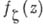, голоморфной в этой области и неограниченно возрастающей при приближении к 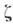Именно является областью голоморфности, если для всюду плотного множества точек ее границы можно построить барьер. Этому условию удовлетворяет, в частности, любая выпуклая область; для любой точки 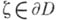достаточно в -мерной опорной плоскости к Dв точке 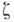выбрать 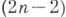-мерную плоскость вида

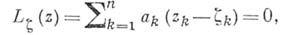
и тогда барьером будет функция 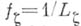. Следовательно, каждая выпуклая область в есть область голоморфности. Однако выпуклость не является необходимым признаком голоморфности: произведение плоских областей всегда есть область голоморфности, а такое произведение может и не быть выпуклым. Тем не менее если надлежащим образом обобщить понятие выпуклости, то можно прийти к необходимому и достаточному признаку. Одно из таких обобщений основано на том, что выпуклую оболочку множества 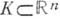можно описать как совокупность точек, в к-рых значение любой линейной функции не превосходит верхней грани значений этой функции на K. По аналогии, голоморфно выпуклой оболочкой множества 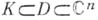наз. совокупность

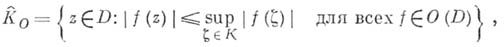
где 0(D).означает множество всех голоморфных в области Dфункций. Область наз. голоморфно выпуклой, если из того, что множество компактно принадлежит D, вытекает, что и 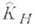компактно принадлежит D. Голоморфная выпуклость является необходимым и достаточным условием области голоморфности. Этот критерий, однако, не очень эффективен, ибо голоморфная выпуклость трудно проверяется.

Другое обобщение связано с понятием плюрисубгар-монической функции, к-рая является комплексным аналогом выпуклой функции. Выпуклую функцию в нек-рой области из 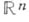можно определить как функцию, сужения к-рой на принадлежащие области отрезки прямых 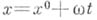(здесь 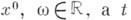- действительный параметр) являются выпуклыми функциями от t. Плюрисубгармонической в области наз. такую полунепрерывную сверху в этой области действительную функцию 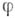, сужение к-рой на принадлежащие Dчасти комплексной прямой 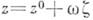( 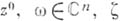- комплексный параметр) является субгармояич. функцией от 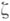. Если 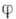дважды непрерывно дифференцируема, то условие ее плюрисубгармоничности по правилу дифференцирования сложных функций выражается условием неотрицательности эрмитовой формы

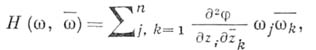
к-рая наз. формой Леви.

Область 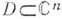наз. псевдовыпуклой, если для нее функция , где 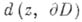означает

евклидово расстояние точки 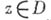до границы , является плюрисубгармонич. в этой области. Псевдовыпуклость также является необходимым и достаточным условием области голоморфности.

В ряде случаев псевдовыпуклость области удается проверить эффективно.

Для областей, не являющихся областью голоморфности, возникает задача описания ее оболочки голоморфности, т. е. наименьшей области голоморфности, в к-рую аналитически продолжается любая функция, голоморфная в 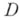. Для областей простейших типов оболочку голоморфности удается построить эффективно. Однако в общем случае задача неразрешима в классе однолистных областей. В процессе аналитич. родолжения функций за пределы заданной области в нек-рых случаях возникает многозначность, для избежания к-рой приходится вводить многолистные области наложения над , аналогичные римановым поверхностям. В классе областей наложения задача построения оболочек голоморфности всегда разрешима. Эта задача также имеет приложения в теоретич. физике, именно - в квантовой теории поля.

Переход от плоскости к комплексному пространству существенно расширяет круг геометрич. вопросов, связанных с голоморфными функциями. В частности, такие функции естественно рассматривать не только в областях, но и накомплексных многообразиях - гладких многообразиях четной действительной размерности, соотношения соседства к-рых биголоморфны. Среди них особую роль играют Штейна, многообразия - естественные обобщения областей голоморфности.

Ряд вопросов анализа сводится к задаче построения в данной области голоморфной функции с заданными нулями или мероморфной функции с заданными полюсами и главными частями лорановских разложений. В плоском случае, согласно теоремам Вейерштрасса и Миттаг-Леффлера и их обобщениям, эти задачи решены для произвольной области. В пространственном случае это не так - разрешимость аналогичных задач, к-рые наз. проблемами Кузена, обусловлена нек-рыми топологич. и аналитич. свойствами рассматриваемых комплексных многообразий.

Центральным пунктом решения проблем Кузена является построение из локально заданных функций с теми или иными свойствами глобальной функции, определенной на всем рассматриваемом многообразии и обладающей теми же локальными свойствами. Для такого рода построений оказались очень хорошо приспособленными методы теории пучков, к-рая возникла в процессе алгебраико-топологич. обработки понятия аналитич. функции и нашла важные применения в самых разных отраслях математики. Решение проблемы Кузена методами теории пучков получено в работах А. Картана (Н. Cartan) и Ж. Серра (J. Serre).

Б. В. Шабот.

Современная теория аналитических функций и их обобщений представляет собой одну из важнейших ветвей анализа, тесно связанную с самыми разнообразными разделами математики и имеющую многочисленнее приложения к теоретич. физике, механике и технике.

Фундаментальные исследования по теории А. ф. и их приложениям принадлежат советским математикам. Широкий интерес к теории функций комплексного переменного в России возник в нач. 20 в. в связи с замечательными исследованиями рус. ученых по приложениям теории А. ф. к различным вопросам механики сплошных сред. Важнейшие задачи гидро-и аэродинамики были решены на базе методов теории А. ф. в трудах Н. Б. Жуковского и С. А. Чаплыгина. В работах Г. В. Колосова и Н. И. Мусхелишвили эти методы нашли глубокие приложения к теории упругости. В последующие годы теория функций комплексного переменного получила в нашей стране всестороннее развитие. Фундаментальные исследования В. В. Го-лубева, Н. Н. Лузина, И. И. Привалова и В. И. Смирнова - по граничным свойствам А. ф., М. А. Лаврентьева - по геометрич. теории функций комплексного переменного (квазиконформные отображения и их приложения к газовой динамике), М. В. Келдыша, М. А. Лаврентьева и Л. И. Седова - по приложениям методов теории А. ф. к задачам механики сплошных сред, Д. Е. Меньшова - по теории моногенности, М. В. Келдыша, М. А. Лаврентьева и С. Н. Мергеляна - по теории приближений функций комплексного переменного, И. Н. Векуа - по теорип обобщенных А. ф. и их приложениям, А. О. Гельфонда - по теории интерполяции, Н. Н. Боголюбова ц В. С. Владимирова - по теории А. ф. нескольких переменных и ее применениям в квантовой теории поля и многие др. сыграли определяющую роль в развитии соответствующих разделов теории А. ф. Теория А. ф. одного и нескольких комплексных переменных и их обобщений продолжает активно развиваться. См. Граничные свойства аналитических функций, Квазиконформное отображение, Граничные задачи теории аналитических функций, Приближение функций комплексного переменного.

Лит.:[1] Привалов И. И., Введение в теорию функций комплексного переменного, 11 изд., М., 1967; [2] Смирнов В. И., Курс высшей математики, 8 изд., т. 3, ч. 2, М., 1969; [3] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1-2, М., 1967-68; [4] Лаврентьев М. А., Шабат Б. В., Методы теории функций комплексного переменного, 4 изд., М., 1973; [5] Голузин Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; [6] Евграфов М. А., Аналитические функции, 2 изд., М., 1968; [7] Свешвиков А. Г., Тихонова. Н., Теория функций комплексной переменной, М., 1967; [8] Фукс Б. А., Теория аналитических функций многих комплексных переменных, 2 изд., ч. 1-2, М., 1962-63; [9] Владимиров В. С., Методы теории функций многих комплексных переменных, М., 1964; [10] Маркушевич А. И., Очерки по истории теории аналитических функций, М.-Л., 1951; [11] Математика в СССР за тридцать лет, 1917-1947, М.- Л., 1948, с. 319-414; [12] Математика в СССР за сорок лет, 1917- 1957, т. 1, М., 1959, с. 381-510; [13] Шабат Б. В., Введение в комплексный анализ, ч. 1-2, 2 изд., М., 1976; [14] Бицадве А. В., Основы теории аналитических функций комплексного переменного, М., 1969. А. А. Гончар. В. В. Шабат.