МЕРОМОРФНАЯ ФУНКЦИЯ

одного комплексного переменного в области (или на римановой поверхности W) - голоморфная функция в области к-рая в каждой особой точке имеет полюс (т. е. -изолированная точка множества не имеющего предельных точек в W, и ). Совокупность M(W) всех М. ф. в W являетсяполем относительно обычных поточечных операций с последующим доопределением в устранимых особенностях.

Отношение любых голоморфных в W функций, , является М. ф. в W. Обратно, всякая М. ф. в области (и на некомпактной римановой поверхности W) представляется в виде где голоморфны и не имеют общих нулей в W. Таким образом, на некомпактной римановой поверхности поле совпадает с полем отношений кольца голоморфных функций в W. Всякая М. ф. определяет непрерывное отображение области в сферу Римана к-рое является голоморфным отображением относительно стандартной комплексной структуры

Обратно, всякое голоморфное отображение определяет М. ф. f в : множество полюсов f совпадает с дискретным множеством и , если . Таким образом, М. ф. одного комплексного переменного можно отождествлять с голоморфными отображениями в сферу Римана.

Основные задачи теории М. ф.- это вопросы существования (и построения) М. ф. с данными особенностями.

I. Задано замкнутое дискретное подмножество и в каждой точке -главная часть разложения Лорана

требуется найти М. ф.с этими главными частями, т. е. такую, что f голоморфна в и голоморфна в окрестности a_v для каждого V.

Если число точек a_v конечно, то (в области ) задача решается тривиально функцией . В общем случае эту задачу решает теорема Миттаг-Леффлера: на всякой некомпактной римановой поверхности существует М. ф. с заданными главными частями На компактной римановой поверхности (напр., на торе) эта задача в общем неразрешима - нужны дополнительные условия согласования главных частей.

Вторую основную задачу удобно формулировать в терминах дивизоров, т. е. отображений таких, что для всякого компакта число точек , в к-рых конечно (число D(z) наз. кратностью Dв точке z). Дивизор наглядно можно записать в виде формальной суммы 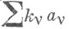, где -точки, в к-рых в случае конечного числа слагаемых число наз. степенью дивизора D. Для М. ф. f ее дивизор (f) равен 0 во всех точках, кроме нулей и полюсов f, где его кратность полагается равной соответственно порядку нуля или полюса (порядки полюсов отрицательны).

II. В точках замкнутого дискретного подмножества заданы "кратности" - целые числа . Требуется найти М. ф. с нулями и полюсами данных кратностей, т. е. такую, что f голоморфна в голоморфна и не равна нулю в окрестности В случае конечного числа точек такой будет, напр., . В общем случае задачу решает теорема Вейерштрасса: на некомпактной римановой поверхности для любого заданного дивизора Dсуществует М. ф. f, дивизор к-рой (f) совпадает с D. Для компактной римановой поверхности голоморфное отображение в сферу Римана, определяемое непостоянной М. ф. f, является разветвленным накрытием, и поэтому каждое значение функция f принимает одинаково часто, в частности число нулей f равно числу ее полюсов (с учетом кратностей). Таким образом, условие необходимо для разрешимости задачи II на компактной римановой поверхности. В общем оно не достаточно; необходимое и достаточное условие существования М. ф. с данным дивизором дает теорема Абеля (см. [2]).

Функции , удовлетворяющие условию для данного дивизора Dна компактной римановой поверхности , образуют конечномерное линейное пространство (над полем ); если , то .

Теорема Римана - Роха утверждает, что

где К - т. н. канонич. дивизор и g-род римановой поверхности . Из этого соотношения получаются многие теоремы существования (если то и, значит, в имеются непостоянные М. ф.). Напр., на всякой компактной римановой поверхности рода существует М. ф., осуществляющая не более чем -листное разветвленное накрытие

Большое место в теории М. ф. одного комплексного переменного занимает распределения значений теория (теория Неванлинны), изучающая распределение корней уравнений при подходе к границе области.

Мероморфная функция нескольких комплексных переменных. Пусть - область в (или комплексное n -мерное многообразие) и - (комплексное) аналитич. подмножество коразмерности 1 (или пустое). Голоморфная функция f, определенная в , наз. мероморфной функцией в , если для каждой точки найдется сколь угодно малая окрестность в и голоморфные в Uфункции без общих необратимых в O(U). множителей такие, что в . Множество наз. полярным мно жеством М. ф. f. Его подмножество , к-рое локально определяется условием наз. множеством (точек) неопределенности М. ф. f; это аналитич. одмножество (комплексной) коразмерности . В каждой точке функция не определена по существу: предельные значения при заполняют всю сферу Римана . С другой стороны, в точках множества существует , и после доопределения для получается голоморфное отображение в сферу Римана. Обратно, если - произвольное комплексное аналитич. одмножество W. коразмерности (возможно, пустое), то любое голоморфное отображение определяет М. ф. в , равную в , где оказывается аналитич. одмножеством коразмерности 1 или пустым. Таким образом, М. ф. f в - это голоморфное отображение в сферу Римана, определенное вне аналитич. одмножества коразмерности Третье, полностью локализованное, определение М. ф. (эквивалентное приведенным выше) формулируется в терминах пучков. Пусть О- пучок ростков голоморфных функций на и для каждой точки есть поле отношений кольца (слоя пучка Онад точкой z). Тогда естественно наделяется структурой пучка полей, к-рый наз. пучком ростков М. ф. в W. М. ф. в W. определяется как глобальное сечение М, т. е. непрерывное отображение такое, что для всех . Множества определяются так: если где , то можно считать, что и взаимно просты, т. е. не имеют общих необратимых в множителей; тогда , если , и , если

Значение так определенной М. ф.в точке , по определению, равно .

Как и в одномерном случае, совокупность всех М. ф. в образует поле относительно поточечных алгебраич. операций с последующим доопределением в устранимых особенностях. Замыкание множества нулей М. ф. f, т. е. множества является аналитич. одмножеством коразмерности 1 (или пустым), множество неопределенности . На и можно определить порядки (кратности) нулей и полюсов М. ф. f. Если р- регулярная точка аналитич. множества , то в нек-рой окрестности множество связно и задается уравнением ,, причем всюду в U. Поэтому существует максимальное целое число такое, что функция голоморфно продолжается в U;. это число наз. порядком (нуля, если , и полюса, если рОР). М. ф. f в точке р. Функция k(р)локально постоянна на множестве регулярных точек . Поэтому каждой М. ф. f в можно сопоставить ее дивизор , где -неприводимые компоненты и -кратность (порядок)в регулярных точках , принадлежащих (другие обозначения:и т. п.). На компактном комплексном многообразии М. ф. определяется своим дивизором однозначно с точностью до постоянного множителя. Задачи, к-рые в одномерном случае решают теоремы Миттаг-Леффлера и Вейерштрасса, в многомерном случае наз. соответственно первой (аддитивной) и второй (мультипликативной) Кузена проблемами. Ввиду сложности полярного множества понятие главной части М. ф. f в общем не определено, и проблемы Кузена формулируются так.

I. Дано открытое покрытие многообразия W и в каждом задана М. ф. f_v; требуется найти М. ф. такую, что для всех .

II. Для данного дивизора на найти М. ф. такую, что .

Условия разрешимости этих задач в многомерном случае гораздо более жесткие, чем в одномерном.

Задача о представлении М. ф. в виде отношения двух голоморфных функций наз. проблемой Пуанкаре. Усиленная проблема Пуанкаре - представимость М. ф. в виде отношения голоморфных функций, ростки к-рых в каждой точке взаимно просты в . Проблема Пуанкаре неразрешима на связном компактном комплексном многообразии, если на нем есть непостоянные М. ф. Однако она разрешима в любой области , более того, в любой области на Штейна многообразии (см. [7]). Разрешимость усиленной проблемы Пуанкаре следует из разрешимости проблемы II Кузена (обратное неверно).

Функции наз. алгебраически зависимым и, если существует многочлен от переменных с комплексными коэффициентами такой, что в общей области определения функций . Максимальное число алгебраически независимых М. ф. на наз. степенью трансцендентности поля . На любом компактном комплексном многообразии это число не превосходит его (комплексной) размерности (теорема 3игеля), более того, это поле имеет конечное число образующих (см. [6]).

На конкретных комплексных многообразиях М. ф. могут обладать дополнительными свойствами. Так, в проективном комплексном пространстве С Р _п множество неопределенности любой непостоянной М. ф. непусто. Всякая М. ф. на проективном алгебраич. многообразии рациональна, т. е. представляется в виде отношения p/q однородных многочленов от однородных координат. На алгебраич. многообразиях поле достаточно богато. С другой стороны, существуют комплексные многообразия (напр., нек-рые неалгебраич. торы), на к-рых всякая М. ф. постоянна. Многомерные обобщения теоремы Римана - Роха не столь эффективны, и теоремы существования различных классов М. ф. получаются лишь для нек-рых классов комплексных многообразий.

См. также Вейерштрасса теорема, Миттаг-Леффлера теорема, Римана- Роха теорема.

Лит.:[1] Неванлинна Р., Однозначные аналитические функции, пер. с нем., М.-Л., 1941; [2] Форстер О., Римановы поверхности, пер. с нем., M._s 1980; [3] Хейман У.-К., Мероморфные функции, пер. с англ., М., 1966; [4] Шабат Б. В., Введение в комплексный анализ, ч. 1-2, М., 1976; [5] Xермандер Л., Введение в теорию функций нескольких комплексных переменных, пер. с англ., М., 1968; [6] Шафаревич И. Р., Основы алгебраической геометрии, М., 1972; [7] Каjiwara J., Sakai К., "Nagoya Math, .т.", 1967, v. 29, р. 75-84.

Е. М. Чирка.