- Дифференциальная геометрия
-
раздел геометрии, в котором геометрические образы изучаются методами математического анализа. Главными объектами Д. г. являются произвольные достаточно гладкие кривые (линии) и поверхности евклидова пространства, а также семейства линий и поверхностей. Обычно в Д. г. исследуются локальные свойства геометрических образов, которые присущи сколь угодно малой их части. Рассматриваются также и свойства геометрических образов в целом (например, свойства замкнутых выпуклых поверхностей).Геометрические объекты, изучаемые в Д. г., обычно подчинены некоторым требованиям гладкости. Как правило, эти требования выражаются в том, что функции, задающие указанные объекты, не менее двух раз непрерывно дифференцируемы.Сущность методов Д. г., применяемых для выяснения локальных свойств геометрических объектов, проще всего уяснить на примере локального исследования формы кривых.В каждой точке М достаточно гладкой кривой L можно построить касательную (См. Касательная) прямую МТ и соприкасающуюся плоскость (См. Соприкасающаяся плоскость) π (рис. 1). При этом касательная МТ является пределом секущей MN при неограниченном приближении точки N к М по кривой L, а соприкасающаяся плоскость есть предел переменной плоскости, проходящей через касательную МТ и точку N при приближении N к М по L. Касательную МТ можно рассматривать также как прямую, наиболее тесно прилегающую к L вблизи точки М. Соприкасающаяся же плоскость представляет собой плоскость, наиболее тесно прилегающую к L вблизи М.Для геометрической характеристики искривлённости кривой L вблизи данной точки М рассматривается Соприкасающаяся окружность, представляющая собой окружность, проходящую через М и наиболее тесно прилегающую к L вблизи М. Это свойство выражается в том, что если учитывать величины только 1-го и 2-го порядка малости по сравнению с длиной дуги MN, то участок кривой L вблизи М можно считать дугой соприкасающейся окружности. Соприкасающаяся окружность касается L в точке М и расположена в соприкасающейся плоскости. Её центр называется центром кривизны кривой L в точке М, а радиус — радиусом кривизны L в М.Для численной характеристики искривлённости L в точке М используется Кривизна k кривой, равная обратной величине радиуса R соприкасающейся окружности: k = 1/R. Кривизну k можно рассматривать и как меру отклонения L от касательной МТ (рис. 1):
 или как скорость изменения (вращения) касательной к L (рис. 2):
или как скорость изменения (вращения) касательной к L (рис. 2): где α — угол между касательными в точках М и N, а Δs — длина дуги MN.Мерой отклонения кривой от соприкасающейся плоскости π в точке М служит так называемое Кручение σ, которое определяется как предел отношения угла β между соприкасающимися плоскостями в точках М и N к длине Δs дуги MN при Δs → 0:
где α — угол между касательными в точках М и N, а Δs — длина дуги MN.Мерой отклонения кривой от соприкасающейся плоскости π в точке М служит так называемое Кручение σ, которое определяется как предел отношения угла β между соприкасающимися плоскостями в точках М и N к длине Δs дуги MN при Δs → 0: При этом угол β берётся со знаком +, если для наблюдателя в М вращение соприкасающейся плоскости в N при приближении N к М происходит против часовой стрелки, и со знаком — в противном случае. Кручение кривой можно рассматривать как скорость изменения (вращения) соприкасающейся плоскости. В частности, для плоской кривой соприкасающаяся плоскость во всех точках совпадает с плоскостью кривой и поэтому кручение такой кривой во всех точках равно нулю. Кривизна k и кручение σ достаточно гладкой кривой L определены в каждой её точке и представляют собой функции параметра, определяющего точки этой кривой. Для вычисления k и σ используется какой-либо способ задания кривой. Чаще всего кривая L задаётся параметрическими уравнениями в прямоугольных координатах:x = φ(t), y = ψ(t), z = χ(t). (1)При изменении параметра t точка М с координатами (x, у, z) описывает кривую L. Иными словами, параметрические уравнения кривой связаны с представлением о кривой как траектории движущейся точки. Правые части (1) могут рассматриваться и как проекции на оси координат радиуса-вектора r переменной точки М кривой L. Вектор r' с координатами {φ'(t), ψ'(t), χ'(t)} называется производной вектор-функции r (t) и направлен по касательной к L в точке М.Кривизна и кручение вычисляются по формулам
При этом угол β берётся со знаком +, если для наблюдателя в М вращение соприкасающейся плоскости в N при приближении N к М происходит против часовой стрелки, и со знаком — в противном случае. Кручение кривой можно рассматривать как скорость изменения (вращения) соприкасающейся плоскости. В частности, для плоской кривой соприкасающаяся плоскость во всех точках совпадает с плоскостью кривой и поэтому кручение такой кривой во всех точках равно нулю. Кривизна k и кручение σ достаточно гладкой кривой L определены в каждой её точке и представляют собой функции параметра, определяющего точки этой кривой. Для вычисления k и σ используется какой-либо способ задания кривой. Чаще всего кривая L задаётся параметрическими уравнениями в прямоугольных координатах:x = φ(t), y = ψ(t), z = χ(t). (1)При изменении параметра t точка М с координатами (x, у, z) описывает кривую L. Иными словами, параметрические уравнения кривой связаны с представлением о кривой как траектории движущейся точки. Правые части (1) могут рассматриваться и как проекции на оси координат радиуса-вектора r переменной точки М кривой L. Вектор r' с координатами {φ'(t), ψ'(t), χ'(t)} называется производной вектор-функции r (t) и направлен по касательной к L в точке М.Кривизна и кручение вычисляются по формулам σ = r'r"r"'/[r', r"]2,в которых [r', r"] — векторное, a r'r "r"' — смешанное произведение (см. Векторное исчисление).С каждой точкой М кривой L связаны три единичных вектора: касательной (t), главной нормали (n) и бинормали (b) (рис. 1). При этом вектор (n) расположен в соприкасающейся плоскости и направлен от точки М к центру кривизны L в М, а вектор b ортогонален t и n и направлен так, что векторы t, n и b образуют правую тройку. Указанная тройка векторов образует так называемый основной, или сопровождающий, триедр кривой L. Плоскости векторов (n, b) и (t, b) называются соответственно нормальной и спрямляющей плоскостями L в М.Формулы для производных векторов t, n, b по длине s дуги L называются формулами Френе. Они играют фундаментальную роль как в теории кривых, так и в приложениях этой теории (в механике, теоретической физике и т.д.). Эти формулы имеют вид
σ = r'r"r"'/[r', r"]2,в которых [r', r"] — векторное, a r'r "r"' — смешанное произведение (см. Векторное исчисление).С каждой точкой М кривой L связаны три единичных вектора: касательной (t), главной нормали (n) и бинормали (b) (рис. 1). При этом вектор (n) расположен в соприкасающейся плоскости и направлен от точки М к центру кривизны L в М, а вектор b ортогонален t и n и направлен так, что векторы t, n и b образуют правую тройку. Указанная тройка векторов образует так называемый основной, или сопровождающий, триедр кривой L. Плоскости векторов (n, b) и (t, b) называются соответственно нормальной и спрямляющей плоскостями L в М.Формулы для производных векторов t, n, b по длине s дуги L называются формулами Френе. Они играют фундаментальную роль как в теории кривых, так и в приложениях этой теории (в механике, теоретической физике и т.д.). Эти формулы имеют вид Если кривизна и кручение не равны нулю в точке М, то можно сделать определённые заключения о форме L вблизи М: проекции L на соприкасающуюся и нормальную плоскости в М имеют вид, изображённый соответственно на рис. 3 и 4. Форма проекции на спрямляющую плоскость зависит от знака кручения. На рис. 5 и 6 изображены проекции L на спрямляющую плоскость для σ > 0 и σ < 0. Кривизна и кручение вполне определяют кривую. Именно, если между точками двух кривых установлено соответствие так, что соответствующие дуги этих кривых имеют одинаковую длину и в соответствующих точках кривые имеют равные кривизны и равные кручения, то эти кривые могут быть совмещены посредством движения.По аналогии с кривыми исследуется локальное строение формы поверхностей. В каждой точке М достаточно гладкой поверхности S можно построить касательную плоскость (См. Касательная плоскость) γ и однозначно определённый соприкасающийся параболоид π (рис. 7), который может выродиться в параболический цилиндр или плоскость. При этом касательную плоскость можно рассматривать как плоскость, наиболее тесно прилегающую к S вблизи М. Соприкасающийся же параболоид характеризуется тем, что в окрестности точки М он совпадает с S с точностью до величин третьего порядка малости по сравнению с размерами этой окрестности. С помощью соприкасающихся параболоидов точки М поверхностей классифицируются следующим образом: эллиптическая (рис. 8) (соприкасающийся параболоид — эллиптический), гиперболическая (рис. 9) (соприкасающийся параболоид — гиперболический), параболическая (рис. 10) (соприкасающийся параболоид — параболический цилиндр), точка уплощения (рис. 11) (соприкасающийся параболоид — плоскость).Обычно для исследования строения поверхности используются так называемая первая и вторая основные квадратичные формы поверхности.Пусть поверхность S определена параметрическими уравнениями:x = φ (u, v), y = ψ (u, v), z = χ (u, v). (2)При фиксированном значении v уравнения (2) определяют на S линию, называемую координатной линией u. Аналогично определяется линия v. Координатные линии u и v образуют на S параметрическую сеть (если, например, сферу радиуса 1 задать параметрическими уравнениямих = cos u cos v, у = cos u sin v, z = sin u,то параметрической сетью линий u и v будут меридианы и параллели этой сферы). Величины u и v называются также внутренними координатами, т.к. точка на поверхности есть точка пересечения проходящих через неё координатных линий, т. е. может быть найдена путём построений на поверхности без обращения к объемлющему пространству.Радиус-вектор r произвольной точки М на S определяется уравнениями (2) как функция u и v. Частные производные ru и rv этой функции суть векторы, касательные соответственно к линиям u и v. Эти векторы в точке М лежат в касательной плоскости к S в М. Векторное произведение [ru, rv] определяет нормаль к S в точке М.Пусть s — длина дуги линии L на S и пусть u = f (t), v = g (t) — параметрические уравнения во внутренних координатах. Тогда, вдоль L r и s будут функциями от t, причём дифференциал s определяется равенством ds2 = dx2 + dy2 + dz2, правая часть которого есть скалярный квадрат вектора dr = rudu + rvdv, т. е. ds2 = dr2. Поэтомуds2 = r2udu2 + 2rurvdudv + r2vdv2.С помощью обозначений r2u = Е, rurv = F, r2v = G выражение для ds2 можно записать в видеds2 = Edu2 + 2Fdudv + Gdv2. (3)Правая часть соотношения (3) называется первой основной квадратичной формой поверхности S. С помощью этой формы можно измерять длины дуг на поверхности путём интегрирования выражения
Если кривизна и кручение не равны нулю в точке М, то можно сделать определённые заключения о форме L вблизи М: проекции L на соприкасающуюся и нормальную плоскости в М имеют вид, изображённый соответственно на рис. 3 и 4. Форма проекции на спрямляющую плоскость зависит от знака кручения. На рис. 5 и 6 изображены проекции L на спрямляющую плоскость для σ > 0 и σ < 0. Кривизна и кручение вполне определяют кривую. Именно, если между точками двух кривых установлено соответствие так, что соответствующие дуги этих кривых имеют одинаковую длину и в соответствующих точках кривые имеют равные кривизны и равные кручения, то эти кривые могут быть совмещены посредством движения.По аналогии с кривыми исследуется локальное строение формы поверхностей. В каждой точке М достаточно гладкой поверхности S можно построить касательную плоскость (См. Касательная плоскость) γ и однозначно определённый соприкасающийся параболоид π (рис. 7), который может выродиться в параболический цилиндр или плоскость. При этом касательную плоскость можно рассматривать как плоскость, наиболее тесно прилегающую к S вблизи М. Соприкасающийся же параболоид характеризуется тем, что в окрестности точки М он совпадает с S с точностью до величин третьего порядка малости по сравнению с размерами этой окрестности. С помощью соприкасающихся параболоидов точки М поверхностей классифицируются следующим образом: эллиптическая (рис. 8) (соприкасающийся параболоид — эллиптический), гиперболическая (рис. 9) (соприкасающийся параболоид — гиперболический), параболическая (рис. 10) (соприкасающийся параболоид — параболический цилиндр), точка уплощения (рис. 11) (соприкасающийся параболоид — плоскость).Обычно для исследования строения поверхности используются так называемая первая и вторая основные квадратичные формы поверхности.Пусть поверхность S определена параметрическими уравнениями:x = φ (u, v), y = ψ (u, v), z = χ (u, v). (2)При фиксированном значении v уравнения (2) определяют на S линию, называемую координатной линией u. Аналогично определяется линия v. Координатные линии u и v образуют на S параметрическую сеть (если, например, сферу радиуса 1 задать параметрическими уравнениямих = cos u cos v, у = cos u sin v, z = sin u,то параметрической сетью линий u и v будут меридианы и параллели этой сферы). Величины u и v называются также внутренними координатами, т.к. точка на поверхности есть точка пересечения проходящих через неё координатных линий, т. е. может быть найдена путём построений на поверхности без обращения к объемлющему пространству.Радиус-вектор r произвольной точки М на S определяется уравнениями (2) как функция u и v. Частные производные ru и rv этой функции суть векторы, касательные соответственно к линиям u и v. Эти векторы в точке М лежат в касательной плоскости к S в М. Векторное произведение [ru, rv] определяет нормаль к S в точке М.Пусть s — длина дуги линии L на S и пусть u = f (t), v = g (t) — параметрические уравнения во внутренних координатах. Тогда, вдоль L r и s будут функциями от t, причём дифференциал s определяется равенством ds2 = dx2 + dy2 + dz2, правая часть которого есть скалярный квадрат вектора dr = rudu + rvdv, т. е. ds2 = dr2. Поэтомуds2 = r2udu2 + 2rurvdudv + r2vdv2.С помощью обозначений r2u = Е, rurv = F, r2v = G выражение для ds2 можно записать в видеds2 = Edu2 + 2Fdudv + Gdv2. (3)Правая часть соотношения (3) называется первой основной квадратичной формой поверхности S. С помощью этой формы можно измерять длины дуг на поверхности путём интегрирования выражения вдоль рассматриваемой дуги. Поэтому форма (3) называется также метрической формой поверхности. Первая форма определяет также внутреннюю геометрию (См. Внутренняя геометрия) поверхности, т. е. совокупность фактов, которые могут быть получены путём измерений на поверхности, без обращения к объемлющему пространству. Внутренняя геометрия поверхности не меняется при её изгибании — деформации поверхности как абсолютно гибкой и нерастяжимой плёнки.Вторая основная квадратичная форма поверхности представляет собой выражениеLdu2 + 2Мdudv + Ndv2,в котором L = ruun, М = ruvn, N = rvvn (n — единичный вектор нормали к S в точке М). С помощью второй формы можно получить представление о пространственной форме поверхности. Например, кривизны 1/R нормальных сечений поверхности в данной точке М (т. е. линий пересечения S с плоскостями, проходящими через нормаль в М) вычисляются по формуле
вдоль рассматриваемой дуги. Поэтому форма (3) называется также метрической формой поверхности. Первая форма определяет также внутреннюю геометрию (См. Внутренняя геометрия) поверхности, т. е. совокупность фактов, которые могут быть получены путём измерений на поверхности, без обращения к объемлющему пространству. Внутренняя геометрия поверхности не меняется при её изгибании — деформации поверхности как абсолютно гибкой и нерастяжимой плёнки.Вторая основная квадратичная форма поверхности представляет собой выражениеLdu2 + 2Мdudv + Ndv2,в котором L = ruun, М = ruvn, N = rvvn (n — единичный вектор нормали к S в точке М). С помощью второй формы можно получить представление о пространственной форме поверхности. Например, кривизны 1/R нормальных сечений поверхности в данной точке М (т. е. линий пересечения S с плоскостями, проходящими через нормаль в М) вычисляются по формуле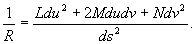 Две основные формы поверхности, заданные в каких-либо внутренних координатах, определяют поверхность с точностью до положения в пространстве. Если заданы две формыEdu2 + 2Fdudv + Gdv2иLdu2 + 2Mdudv + Ndv2,первая из которых положительная, а коэффициенты L, M и N второй удовлетворяют некоторой системе уравнений, из которых одно (полученное К. Гауссом) алгебраическое, а два других (полученные К. М. Петерсоном) — линейные дифференциальные уравнения с частными производными первого порядка, то найдётся поверхность, для которой эти формы являются соответственно первой и второй основными формами.Отмеченные уравнения Гаусса — Петерсона играют фундаментальную роль в теории поверхностей.Подробнее о поверхностях см. Поверхностей теория.Одним из объектов исследований в Д. г. являются семейства кривых и поверхностей. Такие семейства задаются посредством уравнений, содержащих параметры. Например, уравнение (х - α)2 + у2 = 1, содержащее параметр α, определяет семейство окружностей радиуса 1 с центрами в точках (α, 0), т. е. на оси Ox (рис. 12). С семейством кривых (поверхностей) связано понятие огибающей — такой кривой (поверхности), которая касается всех кривых (поверхностей) семейства. В рассмотренном выше примере огибающей будет пара параллельных оси Ox прямых, отстоящих от неё на расстоянии 1. Особенно детально в Д. г. исследованы двупараметрические семейства прямых b в пространстве, называемые конгруэнциями. Простейший пример конгруэнции — семейство параллельных прямых в пространстве. Истоком теории конгруэнций является геометрическая оптика.Различные разделы Д. г. посвящены изучению во всевозможных аспектах так называемых дифференциально-геометрических многообразии (См. Многообразие). Примерами таких многообразий могут служить кривые (одномерные многообразия), поверхности (двумерные многообразия), обычное евклидово пространство (трёхмерное многообразие). Более сложным примером может служить четырёхмерное многообразие, элементами которого являются прямые обычного евклидова пространства (прямая в декартовых координатах определяется уравнениями вида z = ax + b, z = су + d; числа a, b, с, d можно рассматривать как координаты этой прямой).Изучение дифференциально-геометрических многообразий ведётся по следующим основным направлениям. 1) Геометрия транзитивной группы отображений многообразия на себя, или геометрия «локальной группы» отображений. В тематику этих вопросов входят обычная классическая локальная Д. г. (изучение инвариантов группы движений евклидова пространства), аффинная, проективная и конформная геометрии (изучение инвариантов соответствующей группы преобразований). 2) Геометрия многообразий с римановой метрикой (римановых пространств (См. Риманово пространство)), представляющая собой обобщение на многомерный случай внутренней геометрии поверхностей, которое можно рассматривать как двумерные римановы пространства. Геометрия римановых пространств играет важную роль в теории относительности. 3) Геометрия так называемых финслеровых пространств, являющихся обобщением римановых пространств. 4) Геометрия многообразий со связностью, т. е. многообразий, в которых указан способ, с помощью которого можно сравнивать геометрические образы, расположенные в касательных пространствах в разных точках.Возникновение Д. г. связано с именами Л. Эйлера и Г. Монжа. Ими к концу 18 в. были получены важные факты теории поверхностей. Значительный вклад в развитие Д. г. сделан в начале 19 в. К. Гауссом, который ввёл обе основные квадратичные формы. Им же была доказана теорема об инвариантности полной кривизны относительно изометрических преобразований. Фактически им были заложены основы внутренней геометрии поверхностей. Построение основ классической теории поверхностей было завершено в середине 19 в. основателем московской геометрической школы К. М. Петерсоном. В середине и во 2-й половине 19 в. много глубоких и общих результатов по классической теории поверхностей было получено Ф. Миндингом, Ж. Лиувиллем (См. Лиувилль), Э. Бельтрами, Ж. Г. Дарбу, Л. Бианки. Ряд замечательных результатов по классической Д. г. был получен русскими учёными Д. Ф. Егоровым, Н. Н. Лузиным, С. П. Финиковым и др.Развитие др. направлений в Д. г. связано с именами Б. Римана, Г. Ламе, Ф. Клейна, Г. Вейля (См. Вейль), Э. Картана.В СССР разрабатывались различные направления Д. г.; наибольшие успехи относятся к области проблем «в целом» (А. Д. Александров, А. В. Погорелов и др.).Лит.: Монж Г., Приложение анализа к геометрии, пер. с франц., М. — Л., 1936; Стройк Д. Дж., Очерк истории дифференциальной геометрии до XX столетия, пер. с англ., М. — Л., 1941; Погорелов А. В., Дифференциальная геометрия, 5 изд., М., 1969; Рашевский П. К., Курс дифференциальной геометрии, 3 изд., М., 1950; Бляшке В., Введение в дифференциальную геометрию, пер. с нем., М., 1957; Рашевский П. К., Риманова геометрия и тензорный анализ, 2 изд., М., 1964; Александров А. Д., Внутренняя геометрия выпуклых поверхностей, М. — Л., 1948; Погорелов А. В., Внешняя геометрия выпуклых поверхностей, М., 1969.Э. Г. Позняк.
Две основные формы поверхности, заданные в каких-либо внутренних координатах, определяют поверхность с точностью до положения в пространстве. Если заданы две формыEdu2 + 2Fdudv + Gdv2иLdu2 + 2Mdudv + Ndv2,первая из которых положительная, а коэффициенты L, M и N второй удовлетворяют некоторой системе уравнений, из которых одно (полученное К. Гауссом) алгебраическое, а два других (полученные К. М. Петерсоном) — линейные дифференциальные уравнения с частными производными первого порядка, то найдётся поверхность, для которой эти формы являются соответственно первой и второй основными формами.Отмеченные уравнения Гаусса — Петерсона играют фундаментальную роль в теории поверхностей.Подробнее о поверхностях см. Поверхностей теория.Одним из объектов исследований в Д. г. являются семейства кривых и поверхностей. Такие семейства задаются посредством уравнений, содержащих параметры. Например, уравнение (х - α)2 + у2 = 1, содержащее параметр α, определяет семейство окружностей радиуса 1 с центрами в точках (α, 0), т. е. на оси Ox (рис. 12). С семейством кривых (поверхностей) связано понятие огибающей — такой кривой (поверхности), которая касается всех кривых (поверхностей) семейства. В рассмотренном выше примере огибающей будет пара параллельных оси Ox прямых, отстоящих от неё на расстоянии 1. Особенно детально в Д. г. исследованы двупараметрические семейства прямых b в пространстве, называемые конгруэнциями. Простейший пример конгруэнции — семейство параллельных прямых в пространстве. Истоком теории конгруэнций является геометрическая оптика.Различные разделы Д. г. посвящены изучению во всевозможных аспектах так называемых дифференциально-геометрических многообразии (См. Многообразие). Примерами таких многообразий могут служить кривые (одномерные многообразия), поверхности (двумерные многообразия), обычное евклидово пространство (трёхмерное многообразие). Более сложным примером может служить четырёхмерное многообразие, элементами которого являются прямые обычного евклидова пространства (прямая в декартовых координатах определяется уравнениями вида z = ax + b, z = су + d; числа a, b, с, d можно рассматривать как координаты этой прямой).Изучение дифференциально-геометрических многообразий ведётся по следующим основным направлениям. 1) Геометрия транзитивной группы отображений многообразия на себя, или геометрия «локальной группы» отображений. В тематику этих вопросов входят обычная классическая локальная Д. г. (изучение инвариантов группы движений евклидова пространства), аффинная, проективная и конформная геометрии (изучение инвариантов соответствующей группы преобразований). 2) Геометрия многообразий с римановой метрикой (римановых пространств (См. Риманово пространство)), представляющая собой обобщение на многомерный случай внутренней геометрии поверхностей, которое можно рассматривать как двумерные римановы пространства. Геометрия римановых пространств играет важную роль в теории относительности. 3) Геометрия так называемых финслеровых пространств, являющихся обобщением римановых пространств. 4) Геометрия многообразий со связностью, т. е. многообразий, в которых указан способ, с помощью которого можно сравнивать геометрические образы, расположенные в касательных пространствах в разных точках.Возникновение Д. г. связано с именами Л. Эйлера и Г. Монжа. Ими к концу 18 в. были получены важные факты теории поверхностей. Значительный вклад в развитие Д. г. сделан в начале 19 в. К. Гауссом, который ввёл обе основные квадратичные формы. Им же была доказана теорема об инвариантности полной кривизны относительно изометрических преобразований. Фактически им были заложены основы внутренней геометрии поверхностей. Построение основ классической теории поверхностей было завершено в середине 19 в. основателем московской геометрической школы К. М. Петерсоном. В середине и во 2-й половине 19 в. много глубоких и общих результатов по классической теории поверхностей было получено Ф. Миндингом, Ж. Лиувиллем (См. Лиувилль), Э. Бельтрами, Ж. Г. Дарбу, Л. Бианки. Ряд замечательных результатов по классической Д. г. был получен русскими учёными Д. Ф. Егоровым, Н. Н. Лузиным, С. П. Финиковым и др.Развитие др. направлений в Д. г. связано с именами Б. Римана, Г. Ламе, Ф. Клейна, Г. Вейля (См. Вейль), Э. Картана.В СССР разрабатывались различные направления Д. г.; наибольшие успехи относятся к области проблем «в целом» (А. Д. Александров, А. В. Погорелов и др.).Лит.: Монж Г., Приложение анализа к геометрии, пер. с франц., М. — Л., 1936; Стройк Д. Дж., Очерк истории дифференциальной геометрии до XX столетия, пер. с англ., М. — Л., 1941; Погорелов А. В., Дифференциальная геометрия, 5 изд., М., 1969; Рашевский П. К., Курс дифференциальной геометрии, 3 изд., М., 1950; Бляшке В., Введение в дифференциальную геометрию, пер. с нем., М., 1957; Рашевский П. К., Риманова геометрия и тензорный анализ, 2 изд., М., 1964; Александров А. Д., Внутренняя геометрия выпуклых поверхностей, М. — Л., 1948; Погорелов А. В., Внешняя геометрия выпуклых поверхностей, М., 1969.Э. Г. Позняк. Рис. 1 к ст. Дифференциальная геометрия.
Рис. 1 к ст. Дифференциальная геометрия.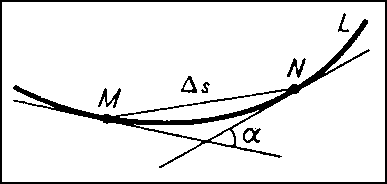 Рис. 2 к ст. Дифференциальная геометрия.
Рис. 2 к ст. Дифференциальная геометрия.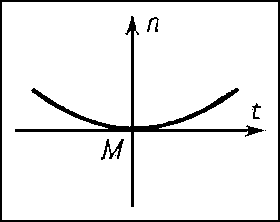 Рис. 3 к ст. Дифференциальная геометрия.
Рис. 3 к ст. Дифференциальная геометрия. Рис. 4 к ст. Дифференциальная геометрия.
Рис. 4 к ст. Дифференциальная геометрия. Рис. 5 к ст. Дифференциальная геометрия.
Рис. 5 к ст. Дифференциальная геометрия.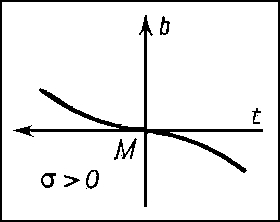 Рис. 6 к ст. Дифференциальная геометрия.
Рис. 6 к ст. Дифференциальная геометрия.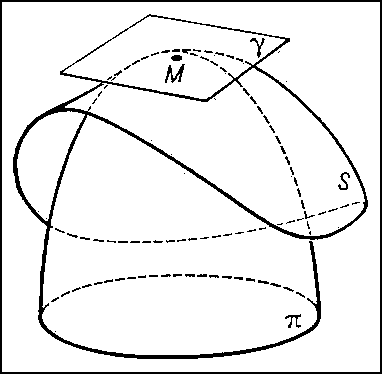 Рис. 7 к ст. Дифференциальная геометрия.
Рис. 7 к ст. Дифференциальная геометрия.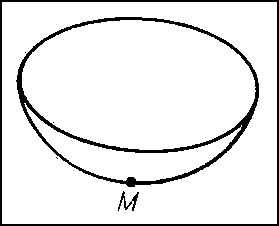 Рис. 8 к ст. Дифференциальная геометрия.
Рис. 8 к ст. Дифференциальная геометрия. Рис. 9 к ст. Дифференциальная геометрия.
Рис. 9 к ст. Дифференциальная геометрия. Рис. 10 к ст. Дифференциальная геометрия.
Рис. 10 к ст. Дифференциальная геометрия. Рис. 11 к ст. Дифференциальная геометрия.
Рис. 11 к ст. Дифференциальная геометрия.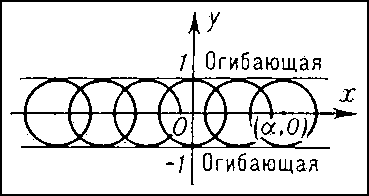 Рис. 12 к ст. Дифференциальная геометрия.
Рис. 12 к ст. Дифференциальная геометрия.
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
