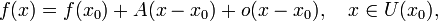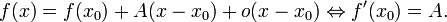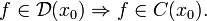Дифференцируемость функции в точке
- Дифференцируемость функции в точке
-
Дифференци́руемая фу́нкция в математическом анализе — это функция, которая может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так и в естественных науках, широко использующих математический аппарат.
Определения
- где o(x − x0) обозначает величину, пренебрежимо малую по сравнению с x − x0 при
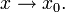 Если f дифференцируема в x0, пишут
Если f дифференцируема в x0, пишут 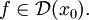
- Линейное отображение
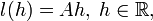 где A — константа из предыдущего определения, называется дифференциа́лом функции f в точке x0 и обозначается df(x0).
где A — константа из предыдущего определения, называется дифференциа́лом функции f в точке x0 и обозначается df(x0).
- Функция z = f(x;y) называется дифференцируемой в точке M(x;y), если ее полное приращение в этой точке можно представить в виде
Δz = AΔx + BΔy + αΔx + βΔy,
где 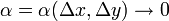 и
и 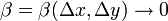 при
при 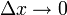 ,
,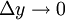
Свойства
- Функция дифференцируема в точке тогда и только тогда, когда у неё существует конечная производная. Более того
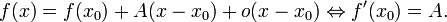
- Дифференциал функции (соответственно производная) определяется единственным образом.
- Функция, дифференцируемая в какой-либо точке, непрерывна в ней же, то есть
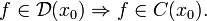
- Обратное, вообще говоря, неверно.
Касательная прямая

График функции (чёрная кривая) и касательная прямая (красная прямая)
-
Из определения дифференцируемой функции вытекает, что она может быть хорошо приближена в окрестности рассматриваемой точки линейной функцией, чей график является прямой. Функция 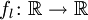 , задаваемая уравнением fl(x) = f(x0) + (f)'(x0)(x − x0), называется касательной к функции f в точке x0.
, задаваемая уравнением fl(x) = f(x0) + (f)'(x0)(x − x0), называется касательной к функции f в точке x0.
Примеры
- Функция f(x) = x2 определена и дифференцируема в любой вещественной точке. Действительно, имеет место представление
- f(x) = f(x0) + 2x0(x − x0) + (x − x0)2.
- Таким образом имеем: f'(x0) = 2x0. Уравнение касательной для этой функции имеет вид:
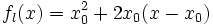 . Дифференциал этой функции задаётся формулой: df(x0)(h) = 2x0h.
. Дифференциал этой функции задаётся формулой: df(x0)(h) = 2x0h.
- Функция f(x) = | x | является непрерывной, но не является дифференцируемой в точке x0 = 0, её производная в этой точке не существует. Соответственно, в этой точке не определён и её дифференциал.
См. также
Ссылки
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Дифференцируемость функции в точке" в других словарях:
Аналитические функции — функции, которые могут быть представлены степенными рядами (См. Степенной ряд). Исключительная важность класса А. ф. определяется следующим. Во первых, этот класс достаточно широк; он охватывает большинство функций, встречающихся в… … Большая советская энциклопедия
Дифференцируемость — Дифференцируемая функция в математическом анализе это функция, которая может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так… … Википедия
Производная функции — У этого термина существуют и другие значения, см. Производная. Иллюстрация понятия производной Производная&# … Википедия
АППРОКСИМАТИВНАЯ ДИФФЕРЕНЦИРУЕМОСТЬ — обобщение понятия дифференцируемости с заменой обычного предела аппроксимативным пределом. Действительная функция действительного переменного наз. аппроксимативно дифференцируемой в точке х 0, если существует такое число А, что При этом величина… … Математическая энциклопедия
Непрерывная дифференцируемость — Дифференцируемая функция в математическом анализе это функция, которая может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так… … Википедия
Показатель Гёльдера — (известен также как показатель Липшица) характеристика гладкости функции. Локальный (точечный) показатель Гёльдера характеризует локальную гладкость (локальную нерегулярность) функции в точке. В общем случае показатель Гёльдера является… … Википедия
Показатель Гельдера — Показатель Гёльдера α (известен также как показатель Липшица) характеристика гладкости функции. Локальный (точечный) показатель Гёльдера характеризует локальную гладкость (локальную нерегулярность) функции в точке. В общем случае показатель… … Википедия
Показатель Липшица — Показатель Гёльдера α (известен также как показатель Липшица) характеристика гладкости функции. Локальный (точечный) показатель Гёльдера характеризует локальную гладкость (локальную нерегулярность) функции в точке. В общем случае показатель… … Википедия
Условие Гельдера — Показатель Гёльдера α (известен также как показатель Липшица) характеристика гладкости функции. Локальный (точечный) показатель Гёльдера характеризует локальную гладкость (локальную нерегулярность) функции в точке. В общем случае показатель… … Википедия
АНАЛИТИЧЕСКАЯ ФУНКЦИЯ — функция, к рая может быть представлена степенным рядом. Исключит, важность класса А. ф. определяется следующим. Во первых, этот класс достаточно ш и р о к: он охватывает большинство функций, встречающихся в основных вопросах математики и ее… … Математическая энциклопедия
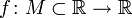 , и
, и 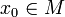 — внутренняя точка области определения f. Тогда f называется дифференци́руемой в x0, если существует окрестность
— внутренняя точка области определения f. Тогда f называется дифференци́руемой в x0, если существует окрестность 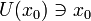 и число
и число 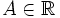 такие, что в этой окрестности для f справедливо представление
такие, что в этой окрестности для f справедливо представление
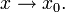 Если f дифференцируема в x0, пишут
Если f дифференцируема в x0, пишут 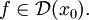
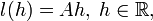 где A — константа из предыдущего определения, называется дифференциа́лом функции f в точке x0 и обозначается df(x0).
где A — константа из предыдущего определения, называется дифференциа́лом функции f в точке x0 и обозначается df(x0).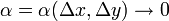 и
и 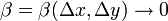 при
при 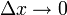 ,
,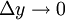
 График функции (чёрная кривая) и касательная прямая (красная прямая)
График функции (чёрная кривая) и касательная прямая (красная прямая)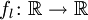 , задаваемая уравнением fl(x) = f(x0) + (f)'(x0)(x − x0), называется касательной к функции f в точке x0.
, задаваемая уравнением fl(x) = f(x0) + (f)'(x0)(x − x0), называется касательной к функции f в точке x0.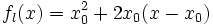 . Дифференциал этой функции задаётся формулой: df(x0)(h) = 2x0h.
. Дифференциал этой функции задаётся формулой: df(x0)(h) = 2x0h.