- Линейная функция
-
Линейная функция — функция вида
 (для функций одной переменной).
(для функций одной переменной).
Основное свойство линейных функций: приращение функции пропорционально приращению аргумента. То есть функция является обобщением прямой пропорциональности.
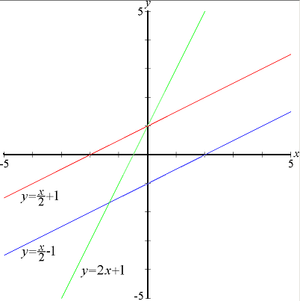
График линейной функции является прямой линией, с чем и связано ее название. Это касается вещественной функции одной вещественной переменной.
- Частный случай
 линейной функции называется однородными линейными функциями (это в сущности синоним прямой пропорциональности), в отличие от
линейной функции называется однородными линейными функциями (это в сущности синоним прямой пропорциональности), в отличие от  — неоднородных линейных функций.
— неоднородных линейных функций.
Содержание
Свойства
 является тангенсом угла, который образует прямая с положительным направлением оси абсцисс.
является тангенсом угла, который образует прямая с положительным направлением оси абсцисс.- При
 , прямая образует острый угол с осью абсцисс.
, прямая образует острый угол с осью абсцисс. - При
 , прямая образует тупой угол с осью абсцисс.
, прямая образует тупой угол с осью абсцисс. - При
 , прямая параллельна оси абсцисс.
, прямая параллельна оси абсцисс.  является показателем ординаты точки пересечения прямой с осью ординат.
является показателем ординаты точки пересечения прямой с осью ординат.- При
 , прямая проходит через начало координат.
, прямая проходит через начало координат.
Линейная функция нескольких переменных
Линейная функция
 переменных
переменных  — функция вида
— функция видагде
 — некоторые фиксированные числа. Областью определения линейной функции является всё
— некоторые фиксированные числа. Областью определения линейной функции является всё  -мерное пространство переменных
-мерное пространство переменных  вещественных или комплексных. При
вещественных или комплексных. При  линейная функция называется однородной, или линейной формой.
линейная функция называется однородной, или линейной формой.Если все переменные
 и коэффициенты
и коэффициенты  — вещественные числа, то графиком линейной функции в
— вещественные числа, то графиком линейной функции в  -мерном пространстве переменных
-мерном пространстве переменных  является
является  -мерная гиперплоскость
-мерная гиперплоскостьв частности при
 — прямая линия на плоскости.
— прямая линия на плоскости.Абстрактная алгебра
Термин «линейная функция», или, точнее, «линейная однородная функция», часто применяется для линейного отображения векторного пространства
 над некоторым полем
над некоторым полем  в это поле, то есть для такого отображения
в это поле, то есть для такого отображения  , что для любых элементов
, что для любых элементов  и любых
и любых  справедливо равенство
справедливо равенствопричём в этом случае вместо термина «линейная функция» используются также термины линейный функционал и линейная форма — также означающие линейную однородную функцию определённого класса.
Алгебра логики
Булева функция
 называется линейной, если существуют такие
называется линейной, если существуют такие  , где
, где  , что для любых
, что для любых  имеет место равенство:
имеет место равенство: .
.
Нелинейные функции
Для функций, не являющихся линейными (то есть достаточно произвольных), когда хотят подчеркнуть некие свойства, употребляют термин нелинейные функции. Обычно это происходит, когда функциональную зависимость вначале приближают линейной, а потом переходят к изучению более общего случая, часто начиная с младших степеней, например рассматривая квадратичные поправки.
То же относится и к употреблению слова нелинейные в отношении других объектов, не обладающих свойством линейности, например — нелинейные дифференциальные уравнения.
В ряде случаев этот термин может применяться и к зависимостям
 , где
, где  , то есть к неоднородным линейным функциям, поскольку они не обладают свойством линейности, а именно в этом случае
, то есть к неоднородным линейным функциям, поскольку они не обладают свойством линейности, а именно в этом случае  и
и  . Например, нелинейной зависимостью считают
. Например, нелинейной зависимостью считают  для материала с упрочнением (см. теория пластичности).
для материала с упрочнением (см. теория пластичности).См. также
Ссылки
- Справочник по математике для инженеров и учащихся втузов. Бронштейн И. Н., Семендяев К. А.- М.: Наука, 1981.- 720с., ил.
Категории:- Элементарные функции
- Булева алгебра
- Линейная алгебра
- Элементарная математика
Wikimedia Foundation. 2010.