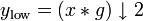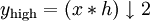Дискретные вейвлет-преобразования

В численном и функциональном анализе дискретные вейвлет-преобразования (ДВП) относятся к вейвлет-преобразованиям, в которых вейвлеты представлены дискретными сигналами (выборками).

Первое ДВП было придумано венгерским математиком Альфредом Хааром. Для входного сигнала, представленного массивом 2ⁿ чисел, вейвлет-преобразование Хаара просто группирует элементы по 2 и образует от них суммы и разности. Группировка сумм проводится рекурсивно (в случае чётной длины последовательности сумм) для образования следующего уровня разложения. В итоге получается 2ⁿ-1 разность и 1 общая сумма.

Это простое ДВП иллюстрирует общие полезные свойства вейвлетов. Во-первых, преобразование (один уровень) можно выполнить за O(n) операций. Во-вторых, оно не только раскладывает сигнал на некоторое подобие частотных полос (путём анализа его в различных масштабах), но и представляет временну́ю область, то есть моменты возникновения тех или иных частот в сигнале. Вместе, эти свойства характеризуют быстрое вейвлет-преобразование — альтернативу обычному быстрому преобразованию Фурье.

Самый распространенный набор дискретных вейвлет-преобразований был сформулирован бельгийским математиком Ингрид Добеши (Ingrid Daubechies) в 1988 году. Он основан на использовании рекуррентных соотношений для вычисления всё более точных выборок неявно заданной функции материнского вейвлета, с удвоением разрешения при переходе к следующему уровню (масштабу). В своей основополагающей работе Добеши выводит семейство вейвлетов, первый из которых является вейвлетом Хаара. С тех пор интерес к этой области быстро возрос, что привело к созданию многочисленных потомков исходного семейства вейвлетов Добеши.

Другие формы дискретного вейвлет-преобразования включают непрореженное вейвлет-преобразование (где не выполняется прореживания сигналов), преобразование Ньюлэнда (где ортонормированный базис вейвлетов выводится из специальным образом построенных фильтров типа «top-hat» в частотной области). Пакетные вейвлет-преобразования также связаны с ДВП. Другая форма ДВП — комплексное вейвлет-преобразование.

У дискретного вейвлет-преобразования много приложений в естественных науках, инженерном деле, математике (включая прикладную). Наиболее широко ДВП используется в кодировании сигналов, где свойства преобразования используются для уменьшения избыточности в представлении дискретных сигналов, часто — как первый этап в компрессии данных.

Определение

Один уровень преобразования

ДВП сигнала x получают применением набора фильтров. Сначала сигнал пропускается через низкочастотный (low-pass) фильтр с импульсным откликом g, и получается свёртка:

$y[n] = (x * g)[n] = \sum\limits_{k = - \infty }^\infty {x[k] g[n - k]}$

Одновременно сигнал раскладывается с помощью высокочастотного (high-pass) фильтра h. В результате получаются детализирующие коэффициенты (после ВЧ-фильтра) и коэффициенты аппроксимации (после НЧ-фильтра). Эти два фильтра связаны между собой и называются квадратурными зеркальными фильтрами (QMF).

Так как половина частотного диапазона сигнала была отфильтрована, то, согласно теореме Котельникова, отсчёты сигналов можно проредить в 2 раза:

$y_{\mathrm{low}} [n] = \sum\limits_{k = - \infty }^\infty {x[k] g[2n - k]}$

$y_{\mathrm{high}} [n] = \sum\limits_{k = - \infty }^\infty {x[k] h[2n - k]}$

Такое разложение вдвое уменьшило разрешение по времени в силу прореживания сигнала. Однако каждый из получившихся сигналов представляет половину частотной полосы исходного сигнала, так что частотное разрешение удвоилось.

Схема разложения сигнала в ДВП^[1]

С помощью оператора прореживания $\downarrow$

$(y \downarrow k)[n] = y[k n]$

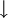
вышеупомянутые суммы можно записать короче:

$y_{\mathrm{low}} = (x*g)\downarrow 2$

$y_{\mathrm{high}} = (x*h)\downarrow 2$

Вычисление полной свёртки x * g с последующим прореживанием — это излишняя трата вычислительных ресурсов.

Схема лифтинга является оптимизацией, основанной на чередовании этих двух вычислений.

Каскадирование и банки фильтров

Это разложение можно повторить несколько раз для дальнейшего увеличения частотного разрешения, с дальнейшим прореживанием коэффициентов после НЧ и ВЧ-фильтрации. Это можно представить в виде двоичного дерева, где листья и узлы соответствуют пространствам с различной частотно-временной локализацией. Это дерево представляет структуру банка (гребёнки) фильтров.

Трехуровневый банк (гребёнка) фильтров

На каждом уровне вышеприведённой диаграммы сигнал раскладывается на низкие и высокие частоты. В силу двукратного прореживания, длина сигнала должна быть кратна 2ⁿ, где n — число уровней разложения.

Например, для сигнала из 32 отсчётов с частотным диапазоном от 0 до f_n трёхуровневое разложение даст 4 выходных сигнала в разных масштабах:

Уровень	Частоты	Длина сигнала
3	0 … fn / 8	4
	fn / 8 … fn / 4	4
2	fn / 4 … fn / 2	8
1	fn / 2 … fn	16

Представление ДВП в частотной области

Пример программы

Ниже приведён пример ДВП-разложения (один уровень), показывающий простоту его вычисления.

Это вейвлет Хаара (Haar wavelet), написанный на

    public static int[] invoke(int[] input){
        //WARNING: This will destroy the contents of the input array
        //This function assumes input.length=2^n, n>1
        int[] output = new int[input.length];
 
        for(int length = input.length >> 1; ; length >>= 1){
        //length=2^n, WITH DECREASING n
            for(int i = 0; i < length; i++) {
                int sum = input[i*2]+input[i*2+1];
                int difference = input[i*2]-input[i*2+1];
                output[i] = sum;
                output[length+i] = difference;
            }
            if (length == 1) 
                return output;
 
            //Swap arrays to do next iteration
            System.arraycopy(output, 0, input, 0, length<<1);
        }
    }