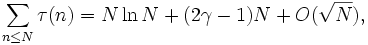- Делитель
-
Делимость — одно из основных понятий арифметики и теории чисел, связаное с операцией деления.
Содержание
Определение
Если для некоторого целого числа a и целого числа
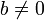 существует такое целое число q, что bq = a, то говорят, что число a делится нацело на b.
существует такое целое число q, что bq = a, то говорят, что число a делится нацело на b.При этом число b называется делителем числа a, делимое a будет кратным числа b, а число q называется частным от деления a на b.
Обозначения
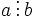 означает, что a делится на b
означает, что a делится на b- b | a означает, что b делит a.
Связанные определения
- Натуральное число, имеющее ровно два натуральных делителя (единицу и само себя), называется простым. Все остальные числа (кроме единицы) называются составными.
- Собственным делителем числа называется всякий его делитель, отличный от самого числа. У простых чисел существует ровно один собственный делитель — единица.
- Вне зависимости от делимости целого числа a на целое число
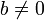 , число a всегда можно разделить на b с остатком, то есть представить в виде:
, число a всегда можно разделить на b с остатком, то есть представить в виде:
- a = bq + r, где
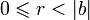 .
.
- a = bq + r, где
- В этом соотношении число r называется остатком (от деления a на b), а число q — неполным частным (от деления a на b).
- Число a делится нацело на b тогда и только тогда, когда остаток от деления a на b равен нулю.
Свойства
- Любое натуральное число является делителем нуля;
- Единица является делителем любого целого числа;
- Любое натуральное число является делителем самого себя.
Число делителей
Число положительных делителей натурального числа n обычно обозначается τ(n), является мультипликативной функцией, для неё верна асимптотическая формула Дирихле:
Обобщения
Понятие делимости обобщается на произвольные кольца, например кольцо многочленов.
См. также
Wikimedia Foundation. 2010.