- Вектор (Геометрические представления)
-
Под направленным отрезком
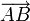 в геометрии понимают упорядоченную пару точек, первая из которых — точка A — называется его началом, а вторая — B — его концом.
в геометрии понимают упорядоченную пару точек, первая из которых — точка A — называется его началом, а вторая — B — его концом.Содержание
Определение
Вектором в простейшем случае называется направленный отрезок, а в других случаях различные векторы — это разные классы эквивалентности направленных отрезков, определяемые неким конкретным отношением эквивалентности. Причем отношение эквивалентности может быть разным, определяя тип вектора («свободный», «фиксированный» итд). Проще говоря, внутри класса эквивалентности все входящие в него направленные отрезки рассматриваются как совершенно равные, и каждый может равно представлять весь класс.
Учитывая изоморфизм между множеством свободных векторов и множеством их параллельных переносов пространства, если операцию сложения отождествить с композицией переносов, можно использовать множество параллельных переносов пространства даже для определения вектора.
Большую роль играют векторы в изучении бесконечно малых трансформаций пространства.
- Вектор, начало которого совпадает с его концом, называют нулевым:
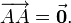
- Вектор
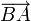 называют противоположным вектору
называют противоположным вектору 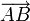 .
.
- Длиной вектора, или модулем вектора, называют длину соответствующего направленного отрезка:
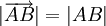 .
.
Свободные, скользящие и фиксированные векторы
Иногда, вместо того, чтобы рассматривать в качестве векторов множество всех равных направленных отрезков, берут только некоторую модификацию этого множества (фактормножество). Так, говорят о «свободных» (когда отождествляются все равные по длине и направлению направленные отрезки, считаясь полностью равными или одним и тем же вектором), «скользящих» (отождествляются между собой все направленные отрезки, равные в смысле свободных векторов, начала и концы которых расположены на одной прямой) и «фиксированных» векторах (по сути дела, просто о направленных отрезках, когда разное начало означает уже неравенство векторов).
Определение. Говорят, что свободные векторы
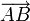 и
и 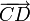 равны, если найдутся точки E и F такие, что четырёхугольники ABFE и CDFE — параллелограммы.
равны, если найдутся точки E и F такие, что четырёхугольники ABFE и CDFE — параллелограммы.- Замечание. «Ухищрение» (введение дополнительных точек) в определении равенства касается, прежде всего, случая, когда точки A,B,C,D располагаются на одной прямой. В противном случае определение выглядит проще:
Определение. Говорят, что свободные векторы
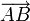 и
и 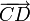 , не лежащие на одной прямой, равны, если четырёхугольник ABDC — параллелограмм.
, не лежащие на одной прямой, равны, если четырёхугольник ABDC — параллелограмм.Определение. Говорят, что скользящие векторы
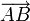 и
и 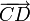 равны, если
равны, если- точки A,B,C,D располагаются на одной прямой,
- векторы
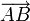 и
и 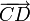 равны между собой как свободные векторы.
равны между собой как свободные векторы.
Неформально говоря, скользящему вектору разрешено двигаться вдоль его прямой без изменения величины и направления.
- Замечание. Скользящие векторы особо употребимы в механике. Простейший пример скользящего вектора в механике — сила. Перенос такого начала вектора вдоль прямой, на котой он лежит, не меняет момента силы ни относительно какой точки; перенос же его на другую прямую, даже если не менять величины и направления вектора, может вызвать изменение его момента (скорее даже почти всегда вызовет): поэтому нельзя рассматривать силу как свободный вектор.
Определение. Говорят, что фиксированные векторы
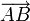 и
и 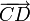 равны, если попарно совпадают точки A и C, B и D.
равны, если попарно совпадают точки A и C, B и D.Операции над векторами
Сложение векторов
 Два вектора u, v и вектор их суммы
Два вектора u, v и вектор их суммыСложение двух свободных векторов можно осуществлять как по правилу параллелограмма, так и по правилу треугольника.
Правило треугольника. Для сложения двух векторов
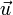 и
и 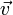 по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора.
по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора.Правило параллелограмма. Для сложения двух векторов
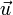 и
и 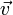 по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.
по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Тогда каждый из векторов переносится вдоль своей прямой в точку пересечения этих прямых, после чего сложение осуществляется по правилу параллелограмма.
Сложение двух фиксированных векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма.
Сложение коллинеарных скользящих векторов
Если скользящие векторы параллельны, то при их сложении главная трудность состоит в определении прямой, на которой будет расположена их сумма. (Величину и направление вектора суммы было бы естественно определить точно так же, как и в случае сложения свободных векторов.) В механике при изучении статики для решения вопроса о сложении параллельных сил, которые, как известно, задаются скользящими векторами, вводится дополнительная гипотеза: к системе векторов можно добавить два вектора, равных по величине, противоположных по направлению и расположенных на одной прямой, пересекающей прямые, на которых расположены данные вектора. Пусть, например, надо сложить скользящие векторы
 и
и 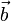 , расположенные на параллельных прямых. Добавим к ним векторы
, расположенные на параллельных прямых. Добавим к ним векторы 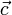 и
и 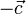 , расположенные на одной прямой. Прямые, на которых расположены векторы
, расположенные на одной прямой. Прямые, на которых расположены векторы  и
и 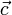 ,
,  и
и 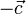 пересекаются. Поэтому определены векторы
пересекаются. Поэтому определены векторы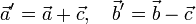
Прямые, на которых расположены векторы
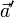 и
и 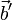 , пересекаются всегда, за исключением случая, когда векторы
, пересекаются всегда, за исключением случая, когда векторы  и
и 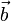 равны по величине и противоположны по направлению, в котором говорят, что векторы
равны по величине и противоположны по направлению, в котором говорят, что векторы  и
и 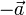 образуют пару (векторов).
образуют пару (векторов).Таким образом, под суммой векторов
 и
и 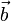 можно понимать сумму векторов
можно понимать сумму векторов 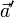 и
и 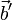 , и эта сумма векторов определена корректно во всех случаях, когда векторы
, и эта сумма векторов определена корректно во всех случаях, когда векторы  и
и 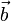 не образуют пару.
не образуют пару.Произведение вектора на число
Произведением вектора
 и числа λ называется вектор, обозначаемый
и числа λ называется вектор, обозначаемый 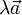 (или
(или 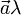 ), модуль которого равен
), модуль которого равен  , а направление совпадает с направлением вектора
, а направление совпадает с направлением вектора  , если
, если 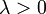 , и противоположно ему, если
, и противоположно ему, если 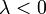 . Если же
. Если же 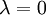 , или вектор
, или вектор  нулевой, тогда и только тогда произведение
нулевой, тогда и только тогда произведение 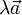 — нулевой вектор.
— нулевой вектор.- Обычно принято в записи произведения числа и вектора число записывать слева, но в принципе допустим и обратный порядок, хотя все же обычное соглашение состоит в том, чтобы его избегать, если нет прямой необходимости. Так или иначе,
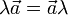 .
.
Из определения произведения вектора на число легко вывести следующие свойства:
- если
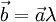 , то
, то 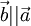 . Наоборот, если
. Наоборот, если 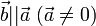 , то при некотором λ верно равенство
, то при некотором λ верно равенство 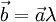 ;
; - всегда
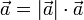 °, то есть каждый вектор равен произведению его модуля на орт.
°, то есть каждый вектор равен произведению его модуля на орт.
Скалярное произведение
Скалярным произведением векторов
 и
и 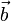 называют число, равное
называют число, равное 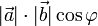 , где
, где 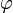 — угол между векторами
— угол между векторами  и
и 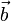 . Обозначения:
. Обозначения: 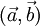 или
или 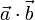 .
.Если один из векторов является нулевым, то несмотря на то, что угол
 не определён, произведение равно нулю.
не определён, произведение равно нулю.Свойства скалярного произведения векторов:
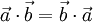 — коммутативность.
— коммутативность.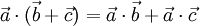 — дистрибутивность.
— дистрибутивность.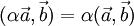 — линейность по отношению к умножению на число.
— линейность по отношению к умножению на число.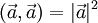 — норма вектора.
— норма вектора.
Геометрически скалярное произведение есть произведение длины одного из сомножителей на ортогональную проекцию другого на направление первого (или наоборот). Скалярное произведение какого-то вектора
 с единичным вектором есть ортогональная проекция вектора
с единичным вектором есть ортогональная проекция вектора  на направление единичного вектора.
на направление единичного вектора.Векторное произведение
Векторным произведением вектора a на вектор b называется вектор c, удовлетворяющий следующим требованиям:
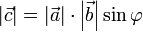
- вектор c ортогонален каждому из векторов a и b
- вектор c направлен так, что тройка векторов abc является правой.
Обозначение:
![\vec c = \left[ \vec a \vec b \right] = \left[ \vec a, \vec b \right] = \vec a \times \vec b](/pictures/wiki/files/56/8a8df77cfa301a9a6e5c4e01235165ad.png)
Геометрически векторное произведение
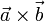 есть ориентированная площадь параллелограмма, построенного на векторах
есть ориентированная площадь параллелограмма, построенного на векторах 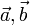 , представленная псевдовектором, ортогональным этому параллелограмму.
, представленная псевдовектором, ортогональным этому параллелограмму.Свойства векторного произведения:
- При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е
- Векторное произведение обладает сочетательным свойством относительно скалярного множителя, то есть
- Векторное произведение обладает распределительным свойством:
Смешанное произведение
Сме́шанное произведе́ние
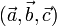 векторов
векторов 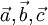 — скалярное произведение вектора
— скалярное произведение вектора  на векторное произведение векторов
на векторное произведение векторов 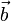 и
и 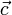 :
:(равенство записано для разных обозначений скалярного и векторного произведения).
Иногда смешанное произведение называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).
Геометрически смешанное произведение
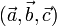 есть (ориентированный) объем параллелепипеда, построенного на векторах
есть (ориентированный) объем параллелепипеда, построенного на векторах 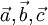 .
.Условие перпендикулярности векторов
Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.
Пример
Даны два вектора
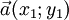 и
и 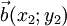 . Эти векторы будут перпендикулярны, если выражение x1x2 + y1y2 = 0.
. Эти векторы будут перпендикулярны, если выражение x1x2 + y1y2 = 0.Условие коллинеарности векторов
Векторы являются коллинеарными тогда и только тогда, когда их векторное произведение равно нулю.
Пример
Даны два вектора
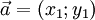 и
и 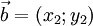 . Эти векторы коллинеарны, если x1 = λx2 и y1 = λy2, где
. Эти векторы коллинеарны, если x1 = λx2 и y1 = λy2, где 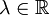
См. также
Ссылки
- Вектор, начало которого совпадает с его концом, называют нулевым:
Wikimedia Foundation. 2010.

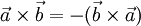
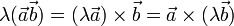
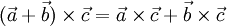
![(\vec{a}, \vec{b}, \vec{c}) = \left(\vec{a}, [\vec{b}, \vec{c}]\right) = \vec{a}\cdot\left(\vec{b}\times\vec{c}\right)](/pictures/wiki/files/50/2def1ecac1759e7c06c5e879e157d6eb.png)