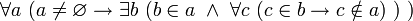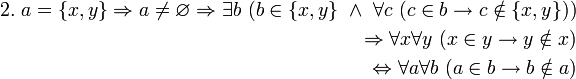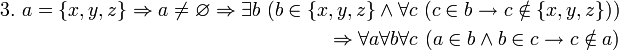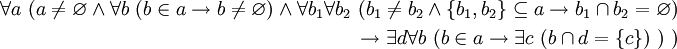- ZFC
-
Современная теория множеств строится на системе аксиом — утверждений, принимаемых без доказательства, из которых выводятся все теоремы и утверждения теории множеств.
Система аксиом Цермело — Френкеля (ZF) является стандартной системой аксиом для теории множеств. Эта и подобные ей системы аксиом любопытны потому, что любая математическая теория может быть «переведена» на язык теории множеств таким образом, что теоремы этой теории станут теоремами о множествах, доказуемыми из аксиом ZF.
К этой системе аксиом часто добавляют аксиому выбора, и называют системой Цермело — Френкеля с аксиомой выбора (ZFC).
Эта система аксиом записана на языке логики первого порядка, и содержит бесконечное количество аксиом. Существуют и другие, конечные системы. Например, система NBG (von Neumann — Bernays — Godel) наряду с множествами рассматривает так называемые классы объектов. NBG равносильна ZF в том смысле, что любая теорема о множествах (то есть не упоминающая о классах), доказуемая в одной системе, также доказуема и в другой.
Содержание
Аксиомы ZFC
Аксиомами ZFC называется следующая совокупность высказываний теории множеств:
Пояснение к аксиомам ZFC
Аксиомы ZFC включают в себя:
0) группу высказываний о равенстве множеств (1 аксиома),
1) группу высказываний о существовании множеств (2 аксиомы),
2) группу высказываний об образовании множеств из уже имеющихся множеств (3 аксиомы и 2 схемы), в которой можно выделить три подгруппы,
3) группу высказываний об упорядоченности образованных множеств (2 аксиомы).
0. Критерий равенства множеств в ZFC
Следующее высказывание выражает необходимое условие идентичности двух множеств.
Аксиома экстенсиональности (Аксиома объёмности)
Примечание
«Аксиому объёмности» можно сформулировать следующим образом: «Если каждый элемент первого множества принадлежит второму множеству, а каждый элемент второго множества принадлежит первому множеству, тогда первое множество идентично второму [множеству].»
Достаточное условие идентичности двух множеств имеет вид
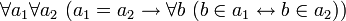 и выводится из аксиом предиката
и выводится из аксиом предиката  , а именно:
, а именно: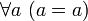 ,
,![~ \forall a_1 \forall a_2 \ (a_1 = a_2 \to (\varphi[a_1] \to \varphi[a_2]))](/pictures/wiki/files/50/297cc0702a68769e668e75031b033d1e.png) , где
, где ![~ \varphi[a_1]](/pictures/wiki/files/99/c5a6859a5ff2d733a4bbb72f2fb9f7bd.png) — любое математически корректное суждение об
— любое математически корректное суждение об 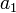 , а
, а ![~ \varphi[a_2]](/pictures/wiki/files/51/36ff804863fade69c1c5c0b6d42e7723.png) — то же самое суждение, но об
— то же самое суждение, но об 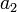 .
.
Соединение указанного достаточного условия [идентичности множеств] с аксиомой объёмности даёт следующий критерий равенства множеств:
1. Аксиомы ZFC о существовании множеств«Аксиома объёмности» была бы бесполезным высказыванием, если бы не существовало ни одного множества или существовало только одно множество.
Следующие два высказывания гарантируют существование по меньшей мере двух разных множеств, а именно: а) множества, в котором нет ничего, и б) множества, в котором должно было бы быть всё [математическое].
Примечание
«Аксиому [существования] пустого множества» можно сформулировать следующим образом: «Существует [по меньшей мере одно] множество без единого элемента.»
Доказывается, что «аксиома пустого множества» равносильна высказыванию
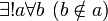 . Поэтому единственному множеству
. Поэтому единственному множеству 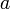 можно присвоить имя. Употребительны два имени:
можно присвоить имя. Употребительны два имени: 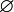 и
и 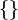 . Используя указанные имена, «аксиому пустого множества» записывают так:
. Используя указанные имена, «аксиому пустого множества» записывают так: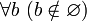 и
и 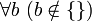
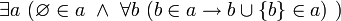 , где
, где 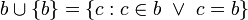
Примечание
«Аксиому бесконечности» можно сформулировать следующим образом: «Существует [по меньшей мере одно] „бесконечное множество“, которое состоит из
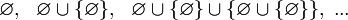 .»
.»Высказывание о существовании бесконечного множества отличается от высказывания о существовании «множества всех множеств» (
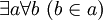 ).
).
2. Аксиомы ZFC об образовании множествСледующие пять высказываний можно назвать аксиомами образования множеств [из имеющихся множеств, включая
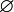 и по меньшей мере одну
и по меньшей мере одну  ].
].Каждое из этих пяти высказываний создано по мотивам высказывания
![~ \forall a \exist b \ (b = \varphi[a])](/pictures/wiki/files/51/3103d56ac2a9b613509eeebb002f62e5.png) , которое выводится из аксиом предиката
, которое выводится из аксиом предиката  .
.Эти пять высказываний можно объединить в следующие подгруппы:
2.0) группу постулатов об образовании множеств путём перечисления их элементов,
2.1) группу деклараций об учреждении и об упразднении семейств множеств,
2.2) группу схем образования множеств с помощью математически корректных суждений.
2.0. Постулаты об образовании множеств путём перечисления их элементовПростейший способ образовать новое множества [из уже имеющихся множеств] состоит в том, чтобы "ткнуть пальцем" в каждое множество, которое должно стать элементом [образуемого множества]. В ZFC указанный способ образования множеств представлен одной аксиомой, в которой "тыканье пальцем" моделируется с помощью предиката
 .
.2.0 Аксиома пары
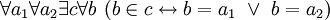 , что есть
, что есть 
Примечание
«Аксиому [неупорядоченной] пары» можно сформулировать следующим образом: «Из любых двух множеств можно образовать „неупорядоченную пару“, то есть такое множество
 , каждый элемент
, каждый элемент  которого идентичен данному множеству
которого идентичен данному множеству 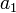 или данному множеству
или данному множеству 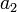 ».
».- Примеры
Доказывается, что «аксиома пары» равносильна высказыванию
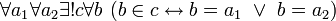 . Поэтому единственному множеству
. Поэтому единственному множеству  можно присвоить имя
можно присвоить имя 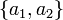 . Используя указанное имя, «аксиому пары» записывают так:
. Используя указанное имя, «аксиому пары» записывают так: или
или 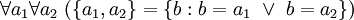
2.1. Декларации об учреждении и об упразднении семейств множествСледующие две аксиомы, именуемые "аксиомой множества подмножеств" и "аксиомой объединения", можно рассматривать как естественное дополнение к "аксиоме пары". Чтобы убедиться в этом, заметим следующее.
Известно, что каждое множество
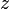 имеет подмножества, включая [копию пустого множества]
имеет подмножества, включая [копию пустого множества] 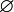 и [копию самого множества]
и [копию самого множества] 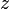 . Иначе говоря,
. Иначе говоря, .
.
Руководствуясь "аксиомой пары", из названных подмножеств можно образовать неупорядоченную пару
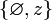 . Назовём эту пару семейством
. Назовём эту пару семейством 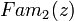 .
.Если можно образовать семейство
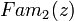 из двух подмножеств множества
из двух подмножеств множества 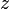 , тогда можно объявить об образовании семейства
, тогда можно объявить об образовании семейства 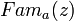 из всех подмножеств множества
из всех подмножеств множества 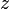 .
.- Чтобы объявить об образовании семейства
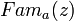 достаточно потребовать, чтобы каждый элемент
достаточно потребовать, чтобы каждый элемент  названного семейства был подмножеством множества
названного семейства был подмножеством множества 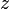 , а каждое подмножество
, а каждое подмножество  названного множества было элементом семейства
названного множества было элементом семейства 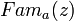 . Иначе говоря,
. Иначе говоря, 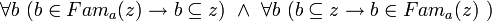 ,
,- что равносильно предложению
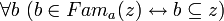 ,
,- которое подразумевает предложение
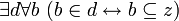 ,
,- которое является частным случаем высказывания
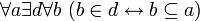 .
.
Если можно объявить об учреждении семейства
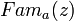 , тогда можно объявить об упразднении названного семейства.
, тогда можно объявить об упразднении названного семейства.- Мыслимы различные способы упразднения семейства
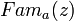 , включая:
, включая: - 1) его полное упразднение (уничтожение), то есть
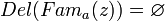 , что равносильно
, что равносильно 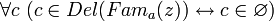 ,
,- 2) его фиктивное упразднение (резервирование), то есть
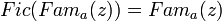 , что равносильно
, что равносильно  ,
,- 3) его реверсивное упразднение (расформирование), то есть
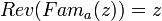 , что равносильно
, что равносильно 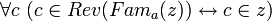 .
.
- Поскольку
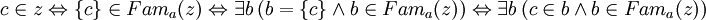 ,
,- постольку предложение
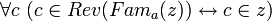
- равносильно предложению
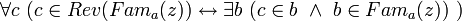 ,
,- которое подразумевает предложение
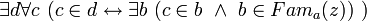 ,
,- которое является частным случаем высказывания
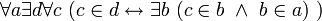 .
.
Из изложенного следует, что высказывания
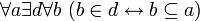 и
и 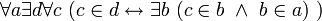 можно считать независимыми условно.
можно считать независимыми условно.2.1.0 Аксиома множества подмножеств (Аксиома булеана)
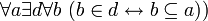 , что есть
, что есть 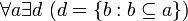 , где
, где 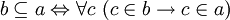
Примечание
«Аксиому множества подмножеств» можно сформулировать следующим образом: «Из любого множества можно образовать „суперкучу“, то есть такое множество
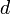 , каждый элемент
, каждый элемент  которого является [собственным либо несобственным] подмножеством
которого является [собственным либо несобственным] подмножеством  данного множества
данного множества 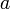 .»
.»- Примеры
 , так как
, так как 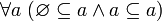
Доказывается, что «аксиома множества подмножеств» равносильна высказыванию
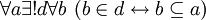 . Поэтому единственному множеству
. Поэтому единственному множеству 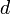 можно присвоить имя
можно присвоить имя 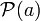 , которое произносится: "множество всех подмножеств [множества]
, которое произносится: "множество всех подмножеств [множества] 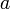 " или "булеан [множества]
" или "булеан [множества] 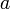 ". Используя указанное имя, «аксиому множества подмножеств» записывают так:
". Используя указанное имя, «аксиому множества подмножеств» записывают так: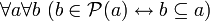 или
или 
2.1.1 Аксиома объединения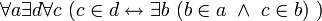 , что есть
, что есть 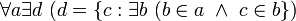
Примечание
Аксиому объединения [множеств] можно сформулировать следующим образом: «Из любого семейства множеств можно образовать „кучу-малу“, то есть такое множество
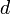 , каждый элемент
, каждый элемент  которого принадлежит по меньшей мере одному множеству
которого принадлежит по меньшей мере одному множеству  данного семейства
данного семейства 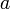 ».
».- Примеры

Доказывается, что аксиома объединения равносильна высказыванию
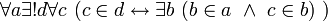 . Поэтому единственному множеству
. Поэтому единственному множеству 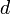 можно присвоить имя
можно присвоить имя  , которое произносится: «объединение множеств семейства
, которое произносится: «объединение множеств семейства 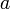 ». Используя указанное имя, аксиому объединения записывают так:
». Используя указанное имя, аксиому объединения записывают так: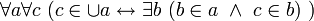 или
или 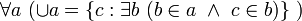 .
.
Объединение множеств семейства
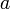 (
( ) не следует путать с пересечением множеств семейства
) не следует путать с пересечением множеств семейства 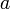 (
(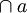 ), о котором известно:
), о котором известно: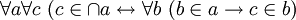 , то есть
, то есть 
2.2. Схемы образования множеств с помощью математически корректных сужденийСреди математических высказываний встречаются аксиомы связи, включая:
а) аксиому связи между алгебраической операцией
 (сложить) и алгебраической операцией
(сложить) и алгебраической операцией  (умножить)
(умножить)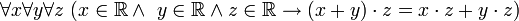 ,
,
б) аксиому связи между отношением порядка
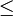 (меньше или равно) и алгебраической операцией
(меньше или равно) и алгебраической операцией  (сложить)
(сложить)
Следующие два высказывания, именуемые "схемой выделения" и "схемой преобразования", являются аксиомами связи между множествами (например, множеством ) и математически корректными суждениями (например, суждением
) и математически корректными суждениями (например, суждением 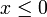 ).
).
"Схема выделения" и "схема преобразования" выражают следующую простую мысль: "Каждое математически корректное суждение об элементах любого множества приводит к образованию [того же самого или другого] множества."
Математически корректные суждения, фигурирующие в "схеме выделения", позволяют "довести [до товарного вида]" множества, которые образованы, например, с помощью аксиомы булеана. Поэтому указанные математические суждения аналогичны штихелям, надфелям, часовым отвёрткам и иным доводочным инструментам.
Математически корректные суждения, фигурирующие в "схеме преобразования", позволяют создавать "[математические] изделия" из ["неотёсанных"] множеств, образованных, например, с помощью аксиомы булеана. Поэтому указанные математические суждения аналогичны прецизионным станкам.
2.2.0 Схема выделения![~ \forall a \exist c \forall b \ (b \in c \leftrightarrow b \in a \ \land \ \Phi[b]\ )](/pictures/wiki/files/54/66a8995e560a9cb006fe7062e355869a.png) , что есть
, что есть ![~ \forall a \exist c \ (c = \{b: b \in a \ \land \ \Phi[b]\} \ )](/pictures/wiki/files/99/c3e0268d917c9cabd73e57f09d802c79.png) , где
, где ![~ \Phi[b]](/pictures/wiki/files/48/041d6391a5452be0db836122c7eb1bde.png) — любое математически корректное суждение о
— любое математически корректное суждение о  , но не о множестве
, но не о множестве 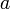 и не о множестве
и не о множестве  .
.
Примечание
Схему выделения [подмножеств] можно сформулировать следующим образом: «Из каждого множества можно выделить [по меньшей мере одно] подмножество
 , высказав суждение
, высказав суждение 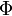 о каждом элементе
о каждом элементе  данного множества
данного множества 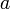 .»
.»- Примеры
![~ 1. \ (\Phi[x] \leftrightarrow x = x) \Rightarrow \forall a \exist c \forall b \ (b \in c \leftrightarrow b \in a \ \land \ b = b)](/pictures/wiki/files/57/93cf53d76c8b4cb33638e464c7f83327.png)
Доказывается. что схема выделения равносильна высказыванию
![~ \forall a \exist!c \forall b \ (b \in c \leftrightarrow b \in a \ \land \ \Phi[b]\ )](/pictures/wiki/files/57/902424db3d4623ffaa1f084f3fa34d49.png) . Поэтому единственному подмножеству
. Поэтому единственному подмножеству  можно присвоить имя
можно присвоить имя ![~ \{x: x \in a \land \Phi[x]\}](/pictures/wiki/files/57/9670cf21a4b10966d9bb2270b37ddcc1.png) . Используя указанное имя, схему выделения записывют так:
. Используя указанное имя, схему выделения записывют так:![~ \forall a \forall b \ (b \in \{x: x \in a \land \Phi[x]\} \leftrightarrow b \in a \ \land \ \Phi[b] \ )](/pictures/wiki/files/101/e577f6079e040e44e9264d19aa0f5c53.png)
- или
![~ \forall a (\{x: x \in a \ \land \ \Phi[x]\} = \{b: b \in a \ \land \ \Phi[b]\}](/pictures/wiki/files/50/2c10539d898fe91a2df8e429ab8ef35d.png)
Схема выделения равносильна счётному множеству аксиом.
2.2.1 Схема преобразования![~ \forall x \exist ! y \ (\phi[x,y]) \ \to \ \forall a \exist d \forall c \ (c \in d \leftrightarrow \exist b \ (b \in a \ \land \ \phi[b,c] \ ) \ )](/pictures/wiki/files/49/1af1e044a1cf56d750c5c2d71d5c385f.png) , что есть
, что есть ![~ \forall x \exist ! y \ (\phi[x,y]) \ \to \ \forall a \exist d \ (d = \{c: \exist b \ (b \in a \ \land \ \phi[b,c])\} \ )](/pictures/wiki/files/100/d6c44cb20973b0adcd959517b85e1e4e.png)
Примечание
Схему преобразования [множеств] можно сформулировать следующим образом: «Любое множество можно преобразовать в [то же самое или другое] множество
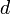 , высказав любое истинное математически корректное функциональное суждение
, высказав любое истинное математически корректное функциональное суждение 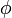 обо всех элементах
обо всех элементах  данного множества
данного множества 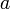 .»
.»- Примеры
![~ 1. \ (\phi[x,y] \leftrightarrow y = x) \Rightarrow \forall a \exist d \forall c \ (c \in d \leftrightarrow \exist b \ (b \in a \ \land \ c = b)) \Leftrightarrow \forall a \exist d \forall c \ (c \in d \leftrightarrow c \in a)](/pictures/wiki/files/97/a84f57cec4ab8f92d4d5275fdc4d6175.png)
Доказывается, что в схеме преобразования множество
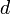 единственно. Поэтому указанному множеству можно присвоить имя
единственно. Поэтому указанному множеству можно присвоить имя ![~ \{y: \exist x \ (x \in a \ \land \ \phi[x,y])\}](/pictures/wiki/files/50/21b31bdf60a4a64e7e33d4ccc16f7d00.png) . Используя указанное имя, схему преобразования записывают так:
. Используя указанное имя, схему преобразования записывают так:![~ \forall x \exist!y (\phi[x,y]) \to \forall a \forall c \ (c \in \{y: \exist x \ (x \in a \ \land \ \phi[x,y])\} \leftrightarrow \exist b \ (b \in a \ \land \ \phi[b,c]) \ )](/pictures/wiki/files/53/51386685890f186408a8af1b82e2a594.png)
- или
![~ \forall x \exist!y (\phi[x,y]) \to \forall a (\{y: \exist x \ (x \in a \ \land \ \phi[x,y])\} = \{c: \exist b \ (b \in a \ \land \ \phi[b,c])\} \ )](/pictures/wiki/files/101/e0ab12beeadb416c35fb3829fc3fe408.png)
Схема преобразования равносильна счётному множеству аксиом.
3. Аксиомы ZFC об упорядоченности множеств
Следующие два высказывания определяют упорядоченность множеств, которые образованы из
 и каждой
и каждой  с помощью аксиом образования множеств. Образно говоря, высказывания об упорядоченности множеств образуют "сортировочный цех" теории ZFC, тогда как высказывания об образовании множеств образуют "производственный цех" этой теории.
с помощью аксиом образования множеств. Образно говоря, высказывания об упорядоченности множеств образуют "сортировочный цех" теории ZFC, тогда как высказывания об образовании множеств образуют "производственный цех" этой теории.Примечание
«Аксиому регулярности» можно сформулировать следующим образом: «В любом семействе множеств есть [по меньшей мере одно] множество
 , каждый элемент
, каждый элемент  которого не принадлежит данному семейству
которого не принадлежит данному семейству 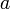 .»
.»- Примеры
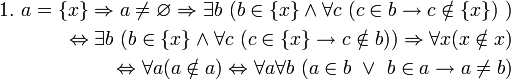
- Сравните с высказываниями
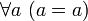 и
и 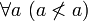 , а также
, а также 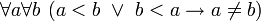 .
.
- Сравните с высказываниями
 и
и 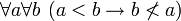 .
.
- Сравните с высказываниями
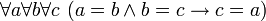 и
и 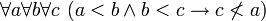 .
.
3.1 Аксиома выбора
Примечание
«Аксиому выбора» можно сформулировать следующим образом: «Из любого семейства непустых попарно непересекающихся множеств можно выбрать „делегацию“, то есть такое множество
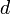 , в котором есть по одному элементу
, в котором есть по одному элементу  от каждого множества
от каждого множества  данного семейства
данного семейства 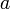 .»
.»- Пример
- Предположим, что семейство образовано из множества неотрицательных чётных чисел и множества неотрицательных нечётных чисел. В таком случае, выполнены все условия "аксиомы выбора", а именно:
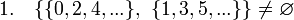 ,
, ,
,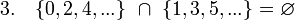 .
.- Следовательно, можно образовать по меньшей мере одну "делегацию" в составе одного "делегата" (например, нуля) от множества
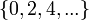 и одного "делегата" (например, единицы) от множества
и одного "делегата" (например, единицы) от множества  . Действительно:
. Действительно: 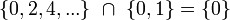 .
.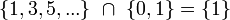 .
.
Примечания
1. Непротиворечивость аксиоматики ZFC не установлена.
Историческая справка
Сведения в этой исторической справке нуждаются в уточнении
По-видимому, первоначальный вариант теории множеств, умышленно названный Немецким математиком Георгом Кантором (Georg Cantor) учением о множествах, состоял из двух аксиом, а именно:
- 1) аксиомы объёмности
 , которая позволяет сформулировать критерий равенства множеств,
, которая позволяет сформулировать критерий равенства множеств,
- 2) "аксиомы математической свободы"
![~ \forall a \exist b \forall c \ (c \in b \leftrightarrow \Phi[a,c])](/pictures/wiki/files/52/445d15217ef3057a41958f57831cc335.png) , которая позволяет создавать множества с помощью "суждения свободы"
, которая позволяет создавать множества с помощью "суждения свободы" ![~ \Phi[a,c]](/pictures/wiki/files/53/50b951b97f9657a5a034053bac254302.png) .
.
"Аксиома математической свободы" имеет рациональные следствия, включая следующие: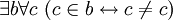 ,
,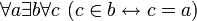 ,
,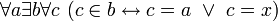 ,
,![~ \forall a \exist b \forall c \ (c \in b \leftrightarrow c \in a \land \Phi[c])](/pictures/wiki/files/56/8572b0b30ca828b71b9ebb1a65c948e1.png) ,
,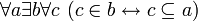 ,
, .
.
В 1903 году Английский философ Бертран Рассел (Bertrand Russel) обратил внимание на следующее:- 1) руководствуясь "аксиомой математической свободы", невозможно отличить "свободу" от "вседозволенности",
- 2) выбрав в качестве
![~ \Phi[a,c]](/pictures/wiki/files/53/50b951b97f9657a5a034053bac254302.png) тривиальнейшее математическое суждение
тривиальнейшее математическое суждение  , мы получаем высказывание о существовании "множества всех множеств"
, мы получаем высказывание о существовании "множества всех множеств" 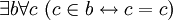 , от которого "один шаг" до парадокса Рассела.
, от которого "один шаг" до парадокса Рассела.
Критические высказывания названного Английского философа о "немецком учении [о множествах]" побудили Немецкого математика Эрнста Цермело (Ernst Zermelo) заменить "аксиому математической свободы" такими её следствиями, которые не вызывали протеста ни у математиков, ни у философов.В 1908 году в журнале Mathematishe Annalen Эрнст Цермело опубликовал следующие семь аксиом:
- 1) Axiom der Bestimmtheit, то есть аксиому объёмности,
- 2) Axiom der Elementarmengen, то есть аксиому о существовании "элементарных множеств"
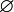 ,
,  и
и 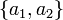 , которую можно записать в следующем виде:
, которую можно записать в следующем виде: 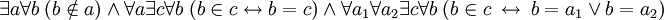 ,
,
- 3) Axiom der Aussonderung, то есть схему выделения,
- 4) Axiom der Potenzmenge, то есть аксиому множества подмножеств,
- 5) Axiom der Vereinigung, то есть аксиому объединения,
- 6) Axiom der Auswahl, то есть аксиому выбора,
- 7) Axiom der Unendlichkeit, то есть аксиому бесконечности в формулировке, отличной от современной формулировки.
Так "учение о множествах" превратилось в теорию множеств, а именно в теорию ZC [Zermelo set theory with the Axiom of Choice].
Последняя аксиома теории ZC (аксиома бесконечности) сблизила сторонников Георга Кантора со сторонниками Леопольда Кронекера, которые рассматривали множество натуральных чисел как священный грааль математики.
как священный грааль математики.Предпоследняя аксиома теории ZC (аксиома выбора) стала предметом оживлённых математических дискуссий. Действительно, эта аксиома не является следствием "аксиомы математической свободы".
В 1922 году Немецкий математик Адольф Френкель (Adolf Fraenkel) и Норвежский математик Торальф Сколем (Thoralf Skolem) дополнили теорию ZC схемой преобразования. В результате теория ZC превратилась в теорию ZFC [Zermelo-Fraenkel set theory with the Axiom of Choice].В 1925 году Венгерский математик Джон фон Нейман (John von Neumann) дополнил теорию ZFC аксиомой регулярности. Одно из следствий этой аксиомы (
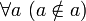 ) "похоронило" и "множество всех множеств", и "парадокс Рассела".
) "похоронило" и "множество всех множеств", и "парадокс Рассела".См. также
- Zermelo-Fraenkel set theory
Литература
- Колмогоров А. Н., Драгалин А. Г. Математическая логика. — М.: УРСС, 2005. — 240 с.
- Френкель А. А., Бар-Хиллел И. Основания теории множеств. — М.: Мир, 1966. — 556 с.
- Аксиоматика теории множеств на сайте (англ.)
Wikimedia Foundation. 2010.

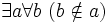
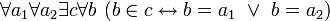
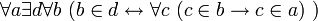
![~ \forall x \exist ! y \ (\phi[x,y]) \to \forall a \exist d \forall c \ (c \in d \leftrightarrow \exist b \ (b \in a \ \land \ \phi[b,c]) \ )](/pictures/wiki/files/49/1731e9cacca82fe36d8bde46e5c84890.png)


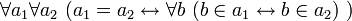
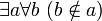
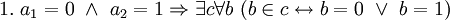
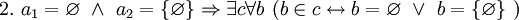
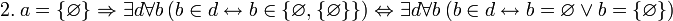
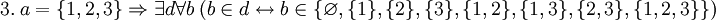
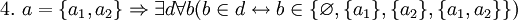
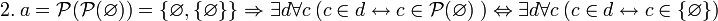

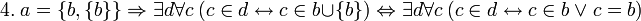
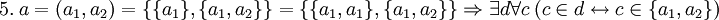
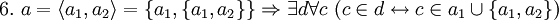
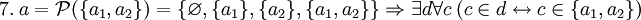
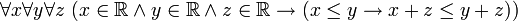
![~ 2. \ (\Phi[x] \leftrightarrow x \ne x) \Rightarrow \forall a \exist c \forall b \ (b \in c \leftrightarrow b \in a \ \land \ b \ne b)](/pictures/wiki/files/57/933ba95e0714c4b0c836eff20bbad848.png)
![~ 3. \ (\Phi[x] \leftrightarrow x \in y) \Rightarrow \forall a \exist c \forall b \ (b \in c \leftrightarrow b \in a \ \land \ b \in y)](/pictures/wiki/files/53/535d58fa8e4cbce21c5915574b79b758.png)
![~ 4. \ (\Phi[x] \leftrightarrow x \notin y) \Rightarrow \forall a \exist c \forall b \ (b \in c \leftrightarrow b \in a \ \land \ b \notin y)](/pictures/wiki/files/101/ee302aa87bbaf99a71134eddf3134f82.png)
![~ 5. \ (\Phi[x] \leftrightarrow x < 2) \ \land \ a = \mathbb{N} \Rightarrow \exist c \forall b \ (b \in c \leftrightarrow b \in \mathbb{N} \ \land \ b < 2) \Leftrightarrow \exist c \forall b \ (b \in c \leftrightarrow b \in \{0,1\})](/pictures/wiki/files/57/9d6ebde48e7bd0746c9890c5bdb73ec0.png)
![\begin{align} 6. \
(\Phi[x] \leftrightarrow \exist k \ (k \in \mathbb{N} \land x = 2k)) \land a = \mathbb{N} \Rightarrow \exist c \forall b \ (b \in c \leftrightarrow b \in \mathbb{N} \land \exist k \ (k \in \mathbb{N} \land b = 2k))
\\ \
\Leftrightarrow \exist c \forall b \ (b \in c \leftrightarrow b \in \{0,2,4,6,...\})
\end{align}](/pictures/wiki/files/98/b0727116ef47508606afb1be6ff1f495.png)
![\begin{align} 7. \
(\Phi[x] \ \leftrightarrow \ \exist u \exist v \ (u \in U \ \land \ v \in V \ \land \ x = (u,v) \ ) \ ) \quad \land \quad a = \mathcal{P}(\mathcal{P}(U \cup V))
\\ \
\Rightarrow \exist c \forall b \ (b \in c \leftrightarrow b \in \mathcal{P}(\mathcal{P}(U \cup V)) \ \land \ \exist u \exist v \ (u \in U \land v \in V \land b = (u,v)))
\end{align}](/pictures/wiki/files/52/41c0a6d82a7a120016a40d2ccbd327d4.png)
![\begin{align} 2. \
(\phi[x,y] \leftrightarrow y = x^2) \ \land \ a = \{1,2,3\} \Rightarrow \exist d \forall c \ (c \in d \leftrightarrow \exist b \ (b \in \{1,2,3\} \ \land \ c = b^2))
\\ \
\Leftrightarrow \exist d \forall c \ (c \in d \leftrightarrow c \in \{1,4,9\})
\end{align}](/pictures/wiki/files/50/2425aa016eef88362a816f214f6f0705.png)
![~ 3. \ (\phi[x,y] \leftrightarrow y = f(x)) \Rightarrow \forall a \exist d \forall c \ (c \in d \leftrightarrow \exist b \ (b \in a \ \land \ c = f(b) \ ) \ )](/pictures/wiki/files/55/7317d9e7a30c28567133ba5be08e2ad7.png)
![\begin{align} 4. \
(\phi[x,y] \leftrightarrow (x = \varnothing \to y = a_1) \land (x \ne \varnothing \to y = a_2) \ ) \quad \land \quad a = \mathcal{P}(\mathcal{P}(\varnothing)) = \{\varnothing, \{\varnothing\}\}
\\ \
\Rightarrow \exist d \forall c \ (c \in d \leftrightarrow \exist b \ (b \in \{\varnothing, \{\varnothing\}\} \land (b = \varnothing \to c = a_1) \land (b \ne \varnothing \to c = a_2)\ ))
\\ \
\Leftrightarrow \exist d \forall c \ (c \in d \leftrightarrow c = a_1 \ \lor \ c = a_2)
\end{align}](/pictures/wiki/files/99/c5bb14b0c297a15d1137ccc22ec6826f.png)
![\begin{align} 5. \
(\phi[x,y] \leftrightarrow y = 2x) \ \land \ a = \mathbb{N} \Rightarrow \exist d \forall c \ (c \in d \leftrightarrow \exist b \ (b \in \mathbb{N} \land c = 2b))
\\ \
\Leftrightarrow \exist d \forall c \ (c \in d \leftrightarrow c \in \{0,2,4,6,...\})
\end{align}](/pictures/wiki/files/51/30f0f864a1e171c485838d5c6059450e.png)
![\begin{align} 6. \
(\phi[x,y] \leftrightarrow y = 2x + 1) \ \land \ a = \mathbb{N} \Rightarrow \exist d \forall c \ (c \in d \leftrightarrow \exist b \ (b \in \mathbb{N} \land c = 2b + 1))
\\ \
\Leftrightarrow \exist d \forall c \ (c \in d \leftrightarrow c \in \{1,3,5,7,...\})
\end{align}](/pictures/wiki/files/54/6316623a316fcedfb05a300077fb3cf8.png)
![\begin{align} 7. \
(\phi[x,y] \leftrightarrow (x \in \mathbb{N} \ \land \ x < 2 \to y = x) \ \land \ (x \in \mathbb{N} \ \land \ \neg (x < 2) \to y = 1)) \quad \land \quad a = \mathbb{N}
\\ \
\Rightarrow \exist d \forall c (c \in d \leftrightarrow \exist b (b \in \mathbb{N} \ \land \ (b \in \mathbb{N} \land b < 2 \to c = b) \ \land \ (b \in \mathbb{N} \land \neg (b < 2) \to c = 1)))
\\ \
\Leftrightarrow \exist d \forall c \ (c \in d \leftrightarrow c \in \mathbb{N} \ \land \ c < 2) \Leftrightarrow \exist d \forall c \ (c \in d \leftrightarrow c \in \{0,1\})
\end{align}](/pictures/wiki/files/56/8965999f79908556c163beba8eb3c331.png)