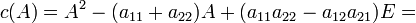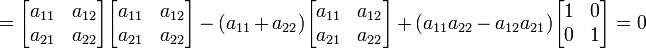Теорема Гамильтона-Кэли

Теорема Гамильтона-Кэли

Теоре́ма Га́мильтона-Кэ́ли — известная теорема из теории матриц, названная в честь Уильяма Гамильтона и Артура Кэли

Теорема Гамильтона-Кэли Любая квадратная матрица удовлетворяет своему характеристическому уравнению. (Если 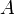$\ A$ — квадратная матрица и 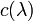$\ c(\lambda)$ её характеристический многочлен, то $\ c(A)=0$.)

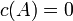Непосредственная проверка оправдывает это утверждение для матрицы порядка 2:

Характеристический многочлен $c(\lambda)=\det(A-\lambda E)=\begin{vmatrix} a_{11}-\lambda & a_{12} \\ a_{21} & a_{22}-\lambda \end{vmatrix}=\lambda^2-(a_{11}+a_{22})\lambda+(a_{11}a_{22}-a_{12}a_{21})$,

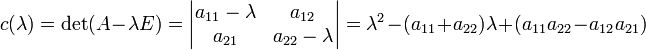тогда

$\ c(A)=A^2-(a_{11}+a_{22})A+(a_{11}a_{22}-a_{12}a_{21})E=$

$=\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}-(a_{11}+a_{22})\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}+(a_{11}a_{22}-a_{12}a_{21})\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}=0$

• Теорема Гамильтона-Кэли обуславливает существование аннулируещего многочлена.
• Теорема Гамильтона-Кэли эквивалентна утверждению, что характеристический многочлен делится без остатка на минимальный многочлен.

Доказательство  

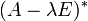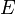Рассмотрим присоединённую λ-матрицу $\ (A-\lambda E)^*$, где $\ E$ — единичная матрица, тогда согласно определению присоединённой матрицы

$\ (A-\lambda E)^*(A-\lambda E)=(A-\lambda E)(A-\lambda E)^*=\det(A-\lambda E)E=c(\lambda)E$.

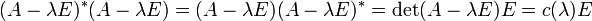Это означает, что λ-матрица 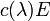$\ c(\lambda)E$ делится без остатка на 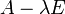$\ A-\lambda E$, а значит, согласно следствию из теоремы Безу для λ-матриц 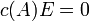$\ c(A)E=0$, и следовательно $\ c(A)=0$.

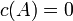См. также

• Матрица (математика)
• Функции от матриц
• Минимальный многочлен
• Характеристический многочлен матрицы
• Аннулирующий многочлен
• λ-матрицы

Литература

• Гантмахер Ф. Р.Теория матриц (2-е изд.). М.: Наука, 1966
• Ланкастер П. Теория матриц М.: Наука, 1973