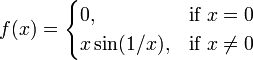Абсолютно непрерывная функция
- Абсолютно непрерывная функция
-
Абсолютно непрерывная функция
Функция 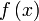 называется абсолю́тно непреры́вной фу́нкцией на конечном или бесконечном отрезке, если
называется абсолю́тно непреры́вной фу́нкцией на конечном или бесконечном отрезке, если 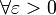 ,
, 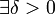 такое, что для любого конечного набора непересекающихся интервалов
такое, что для любого конечного набора непересекающихся интервалов  области определения функции
области определения функции 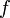 , который удовлетворяет условию
, который удовлетворяет условию 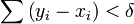 , выполнено
, выполнено 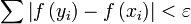 .
.
Абсолютно непрерывная на отрезке функция является равномерно непрерывной, и, следовательно, непрерывной. Обратное неверно.
Свойства абсолютно непрерывных функций
- Всякая абсолютно непрерывная функция имеет на промежутках конечной длины ограниченную вариацию.
- Абсолютно непрерывные функции образуют векторное пространство. Более того, они образуют замкнутое подпространство в пространстве функций ограниченной вариации.
- Произведение абсолютно непрерывных на отрезке конечной длины функций даёт абсолютно непрерывную функцию.
- Каждая абсолютно непрерывная функция представима в виде разности двух неубывающих абсолютно непрерывных функций.
- (Лебег) Если F абсолютно непрерывна на (a,b), то F' является интегрируемой, и для почти всех
![x\in[a,b]](http://dic.academic.ru/pictures/wiki/files/56/8290bddba5acf9822dcbf61f4ac67d1b.png)
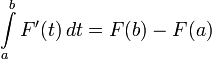 .
.
Примеры
Следующие функции являются непрерывными, но не абсолютно непрерывными:
-
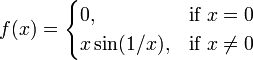
- на конечных интервалах, содержащих 0;
- функция ƒ(x) = x 2 на неограниченных интервалах.
Литература
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Абсолютно непрерывная функция" в других словарях:
Абсолютно — Абсолютный (лат. absolutus законченный, неограниченный, безусловный, совершенный) абсолютный означает то, что рассматривается само по себе, без отношения к чему либо другому, противопоставляется относительному. Значения В философии: Абсолютная… … Википедия
Абсолютно непрерывное распределение — Плотность вероятности один из способов задания вероятностной меры на евклидовом пространстве . В случае когда вероятностная мера является распределением случайной величины, говорят о плотности случайной величины. Содержание 1 Плотность… … Википедия
Функция — I Функция (от лат. functio совершение, исполнение) (философская), отношение двух (группы) объектов, в котором изменение одного из них ведёт к изменению другого. Ф. может рассматриваться с точки зрения следствий (благоприятных,… … Большая советская энциклопедия
Функция ограниченной вариации — В математическом анализе вариацией функции называется числовая характеристика функции одного действительного переменного, связанная с её дифференциальными свойствами. Для функции из отрезка на вещественной прямой в является обобщением понятия… … Википедия
СИНГУЛЯРНАЯ ФУНКЦИЯ — отличная от постоянной непрерывная ограниченной вариации функция, производная к рой почти всюду на рассматриваемом отрезке равна нулю. С. ф. входят в качестве слагаемых в Лебега разложение функций ограниченной вариации. Напр., всякая непрерывная… … Математическая энциклопедия
Функция (математ.) — Функция, одно из основных понятий математики, выражающее зависимость одних переменных величин от других. Если величины x и у связаны так, что каждому значению x соответствует определённое значение у, то у называют (однозначной) функцией аргумента … Большая советская энциклопедия
СЛОЖНАЯ ФУНКЦИЯ — функция, представленная как композиция нескольких функций. Если множество значений Yi функции fi содержится во множестве определения Х i+1 функции fi+1, т. е. то функция определяемая равенством наз. сложной функцией или (п 1) кратной композицией… … Математическая энциклопедия
ВЫПУКЛАЯ ФУНКЦИЯ — действительного переменного функция , определенная на нек ром интервале, для любых двух точек х 1 и x2 к рого выполняется условие Геометрически это означает, что середина любой хорды графика функции f лежит либо над графиком, либо на нем. Если… … Математическая энциклопедия
РАСПРЕДЕЛЕНИЯ ФУНКЦИЯ — к а к о й л и б о с л у ч а й н о й в е л и ч и н ы X функция действительного переменного х, принимающая при каждом хзначение, равное вероятности неравенства Х<x. Каждая Р. ф. F(х)обладает следующими свойствами: 1) при ; 2) F(х)непрерывна… … Математическая энциклопедия
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ — 1) А. н. интеграла свойство неопределенного интеграла (Лебега). Пусть функция f интегрируема на множестве Е. Интеграл от f на измеримых подмножествах является абсолютно непрерывной функцией (см. ниже п. 3) множества относительно меры m, т. е. для … Математическая энциклопедия
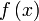 называется абсолю́тно непреры́вной фу́нкцией на конечном или бесконечном отрезке, если
называется абсолю́тно непреры́вной фу́нкцией на конечном или бесконечном отрезке, если 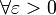 ,
, 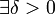 такое, что для любого конечного набора непересекающихся интервалов
такое, что для любого конечного набора непересекающихся интервалов  области определения функции
области определения функции 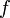 , который удовлетворяет условию
, который удовлетворяет условию 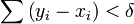 , выполнено
, выполнено 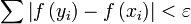 .
.![x\in[a,b]](http://dic.academic.ru/pictures/wiki/files/56/8290bddba5acf9822dcbf61f4ac67d1b.png)
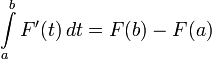 .
.