ВЫПУКЛАЯ ФУНКЦИЯ

действительного переменного - функция , определенная на нек-ром интервале, для любых двух точек х ₁ и x₂ к-рого выполняется условие

Геометрически это означает, что середина любой хорды графика функции f лежит либо над графиком, либо на нем. Если для любых и неравенство (1) является строгим неравенством, то функция f называется строго выпуклой. Примеры В. ф.: для для всех х. При обратном знаке неравенства (1) функцию f наз. вогнутой. Всякая измеримая В. ф. непрерывна. Существуют В. ф., не являющиеся непрерывными, но они очень нерегулярны: если функция f выпукла на интервале ( а, b).и ограничена сверху в некотором интервале, лежащем внутри ( а, b), то она непрерывна на ( а, b). Таким образом разрывная В. ф. неограничена на каждом внутреннем интервале и неизмерима.

Если функция f непрерывна на интервале и на каждой хорде ее графика имеется по крайней мере одна точка, отличная от концов хорды и лежащая над графиком или на нем, то функция f выпукла. Из условия (1) для непрерывной функции f вытекает, что центр тяжести любого конечного числа материальных точек, лежащих на графике функции, находится либо над ее графиком, либо на нем: для любых чисел ( п - произвольно) справедливо неравенство

называемое Иенсена неравенством.

Если для нек-рой функции f неравенство (2) выполняется для любых двух точек нек-рого интервала и любых то функция f непрерывна и, конечно, выпукла на этом интервале. Любая хорда графика непрерывной В. ф. либо совпадает с соответствующей его частью, либо, за исключением его концов, целиком лежит над графиком. Это означает, что если непрерывная В. ф. не является линейной ни на каком интервале, то в неравенствах (1) и (2) для любых попарно различных значений аргумента выполняется строгое неравенство, и значит f является строго В. ф.

Непрерывная функция выпукла тогда и только тогда, когда множество точек плоскости, лежащих над ее графиком, т. е. ее надграфик является выпуклым множествам. Для того чтобы непрерывная функция f, определенная на интервале ( а, b), была выпукла, необходимо и достаточно, чтобы через каждую точку ее графика проходила по крайней мере одна прямая (наз. опорной прямой), лежащая либо под графиком [над интервалом (а, b)], либо частично на графике, т. е. чтобы для любой точки существовало такое , что

для всех .

Непрерывная выпуклая на интервале функция не имеет строгого локального максимума. Если функция f непрерывна и выпукла на интервале (а, b), то в каждой его точке х _й она имеет левую и правую конечные производные, причем и, более того, если число удовлетворяет условию (3), то 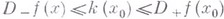. Функции и не убывают п во всех точках, за исключением, быть может, счетного числа их, совпадают , и тем самым функция f является дифференцируемой в этих точках. На каждом отрезке, лежащем внутри ( а, b), функция f удовлетворяет условию Липшица и, следовательно, является абсолютно непрерывной. Это позволяет установить следующий критерий выпуклости: непрерывная функция выпукла тогда и только тогда, когда она является неопределенным интегралом от неубывающей функции.

Если функция f дифференцируема на интервале, то для того чтобы она была (строго) выпуклой на нем. необходимо и достаточно, чтобы ее производная (возрастала) не убывала. В точке графика непрерывной В. ф., соответствующей точке, в к-рой функция дифференцируема, существует единственная опорная прямая - касательная в этой точке. С другой стороны, если у дифференцируемой на интервале функции для каждой точки ее графика касательная к графику в этой точке в нек-рой окрестности точки касания лежит (за исключением точки касания) под графиком, то функция строго выпукла, если же она лежит либо под графиком функции, либо частично на нем, то - просто выпукла.

Если функция f дважды дифференцируема на интервале, то для того чтобы она была выпукла на нем, необходимо и достаточно, чтобы ее вторая производная была неотрицательна на этом интервале (утверждение остается справедливым, если под второй производной понимать не обычную производную, а симметрическую производную). Если функция в каждой точке нек-рого интервала имеет положительную вторую производную, то функция строго выпукла на этом интервале.

Если функции выпуклы на интервале то функция

также выпукла на том же интервале, причем если хотя бы одна из функций 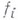строго выпукла, то и функция f строго выпукла. Определение и свойства В. ф. на интервале переносятся и на промежутки других видов: отрезки и полуинтервалы.

Имеются различные обобщения понятия выпуклости на функции многих переменных. Пусть, напр., функция определена на выпуклом множестве М n -мерного аффинного пространства . Функция f наз. выпуклой, если для любых точгк и выполняется неравенство (1), где под понимается сумма n-мерных векторов . Свойства В. ф. одного переменного соответствующим образом обобщаются на функции многих переменных: напр., для непрерывных В. ф. 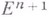и в этом случае выполняется неравенство (2), непрерывная функция выпукла тогда и только тогда, когда множество точек пространства , лежащих над ее графиком, выпукло.

Для того чтобы непрерывная функция f, определенная на выпуклой области G, была выпуклой, необходимо и достаточно, чтобы для любой точки существовала такая линейная функция

что

Гиперплоскость, задаваемая уравнением наз. опорной.

Если функция f непрерывно дифференцируема в G, то условие (4) эквивалентно условию

Если функция f дважды непрерывно дифференцируема, то условие (4) эквивалентно условию неотрицательности второго дифференциала функции f, т. е. квадратичной формы

для всех .

Другим важным обобщением понятия В. ф. для функций многих переменных является понятие субгармонической функции. Понятие В. ф. естественным образом обобщается на функции, определенные на соответствующих подмножествах бесконечномерных линейных пространств, см. Выпуклый функционал.

Лит.:[1] Бурбаки Н., Функции действительного переменного, пер. с франц.. М., 1965, гл. 1, § 4; [2] Зигмунд А., Тригонометрические ряды, пер. с англ., М., 1965, гл. 1;[3] Кудрявцев Л. Д., Математический анализ, 2 изд., т. 1, М., 1973, гл. 1; [4] Натанеон И. П..Теория функций вещественной переменной, 3 изд., М., 1974, гл. 10; [5] Никольский С. М., Курс математического анализа, М., 1973, гл. 5; [6] Xарди Г. Г., Литтльвуд Дж. Е., Полиа Г., Неравенства, пер. с англ., М., 1948. гл. 3. Л. Д. Кудрявцев.