Седловая точка

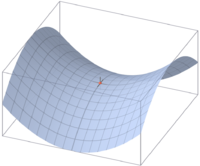
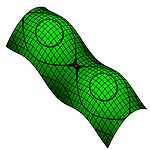
Седловая точка функции z=x²-y² (обозначена красным)

Седловая точка на карте высот (центр «восьмерки» образованной изолиниями)

Седловая точка в математическом анализе — такая точка из области определения функции, которая является стационарной для данной функции, однако не является её локальным экстремумом. В такой точке, если рассматривается функция двух переменных, образованная графиком функции поверхность обычно напоминает по форме седло или горный перевал — выпуклая в одном направлении и вогнутая в другом. На карте высот седловая точка может быть в общем случае обнаружена в месте пересечения изолиний. Например, два холма, между которыми находится высокий перевал, образуют седловую точку в вершине этого перевала: на карте высот это будет выглядеть как центр «восьмерки», образованной соответствующими изолиниями.

Седловая точка в математическом анализе

Проверить, является ли данная стационарная точка функции F(x,y) двух переменных седловой, можно, вычислив матрицу Гессе функции в этой точке: если гессиан будет неопределенной квадратичной формой, то данная точка — седловая. Например, составив матрицу Гессе функции $z=x^2-y^2$ в стационарной точке $(0, 0)$ получим матрицу:

$\begin{bmatrix} 2 & 0\\ 0 & -2 \\ \end{bmatrix}$

которая является неопределенной. Поэтому, точка $(0, 0)$ данной функции — седловая. Однако вышеприведенный критерий предоставляет только достаточное условие наличия седловой точки. Например, $(0, 0)$ является седловой точкой функции $z=x^4-y^4$, но матрица Гессе в данном случае будет нулевой матрицей, которую, по определению, нельзя назвать неопределенной.

В общем случае, седловой точкой гладкой функции (график которой изображает кривую, поверхность или гиперповерхность) называется такая стационарная точка, в окрестности которой данная кривая/поверхность/гиперповерхность не лежит полностью по одну сторону касательного пространства в данной точке.

График y = x³ с седловой точкой в 0

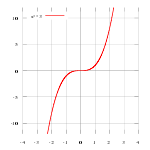
В случае функции одной переменной, седловая точка — такая точка, которая одновременно является и стационарной точкой, и точкой перегиба (точка перегиба не является локальным экстремумом).

Седловая точка матрицы

Седловой точкой (седловым элементом) матрицы $A = (a_{i, j})_{i = 1, j = 1}^{m, n}$ называют элемент матрицы $a_{k, l}$, удовлетворяющий условиям $a_{k, l} = \max_{1 \le j \le m}\ \min_{1 \le i \le n}a_{i, j} = \min_{1 \le i \le n}\ \max_{1 \le j \le m}a_{i, j}$, то есть элемент матрицы, который одновременно является минимальным элементом в соответствующей строке матрицы и максимальным элементом в соответствующем столбце матрицы, или же наоборот, то есть элемент матрицы, который одновременно является максимальным элементом в соответствующем столбце матрицы и минимальным элементом в соответствующей строке матрицы.

Примеры

Матрица

$\begin{bmatrix} 5 & 6 & 4 & 5\\ -2 & 5 & 3 & 7\\ 8 & 7 & -2 & 6\\ \end{bmatrix}$

имеет 1 седловой элемент, равный 4, который расположен в первой строке в третьем столбце матрицы, так как он одновременно является минимальным элементом в соответствующей строке матрицы (в данном случае в первой строке матрицы) и максимальным элементом в соответствующем столбце матрицы (в данном случае в третьем столбце матрицы).

Матрица

$\begin{bmatrix} 2 & 3 & 5 & 2\\ 2 & 4 & 6 & 2\\ -2 & 7 & 2 & 0\\ \end{bmatrix}$

имеет 4 седловых элемента, равных 2, которые расположены в первой строке в первом столбце, в первой строке в четвёртом столбце, во второй строке в первом столбце, во второй строке в четвёртом столбце матрицы, соответственно.

Данный пример показывает, что матрица может иметь несколько (более одной) седловых точек.

Если матрица имеет несколько седловых точек, то все их значения равны.

Так, в матрице, все элементы которой равны друг другу, все элементы являются седловыми точками.

Матрица

$\begin{bmatrix} 3 & 2 & 1\\ 1 & 3 & 4\\ \end{bmatrix}$

не имеет седловой точки.

Применение

Вышеприведенное использование термина «седловая точка» имеет особое значение в теории игр. Так, например, в играх с нулевой суммой седловая точка платёжной матрицы является равновесием Нэша.

См. также

• Критическая точка (математика)
• Метод перевала
• Экстремум
• Особая точка (дифференциальные уравнения)
• Матрица (математика)

Литература

• Gray, Lawrence F.; Flanigan, Francis J.; Kazdan, Jerry L. & Frank, David H (1990), «Calculus two: linear and nonlinear functions», Berlin: Springer-Verlag, сс. page 375, ISBN 0-387-97388-5 
• Гильберт Д., Кон-Фоссен С., Наглядная геометрия. — URSS, Пер. с нем., Изд.5, 2010. 344
• von Petersdorff, Tobias (2006), "Critical Points of Autonomous Systems", «Differential Equations for Scientists and Engineers (Math 246 lecture notes)», <http://www.wam.umd.edu/~petersd/stab.html> 
• Widder, D. V. (1989), «Advanced calculus», New York: Dover Publications, сс. page 128, ISBN 0-486-66103-2