Элемент (математика)

Мно́жество — один из ключевых объектов математики, в частности, теории множеств. «Под множеством мы понимаем объединение в одно целое определенных, вполне различимых объектов нашей интуиции или нашей мысли» (Г. Кантор). Это не является в полном смысле логическим определением понятия множество, а всего лишь пояснением (ибо определить понятие — значит найти такое родовое понятие, в которое данное понятие входит в качестве вида, но множество — это, пожалуй, самое широкое понятие математики и логики).

В математической логике и дискретной математике часто употребляемый синоним множества — алфавит.

Теории

Существует два основных подхода к понятию множества — наивная и аксиоматическая теория множеств.

«Наивная теория множеств»

Дать определение какому-нибудь понятию — это значит описать это понятие через понятия, определённые ранее. Если число определений в теории конечно, то первое определение должно быть основано на понятиях, которые являются аксиоматическими, то есть изначально неопределёнными. Множество — как раз одно из таких аксиоматических понятий. В рамках наивной теории множеств множеством считается любой чётко определённый набор объектов (элементов множества). Вольное использование наивной теории множеств приводит к некоторым парадоксам, возникающим из-за того, что интуитивное понятие «чётко определённый» на самом деле само не определено чётко. Так как теория множеств, фактически, используется как основание и язык всех современных математических теорий, становится очевидной необходимость её строгой аксиоматизации.

Наивная теория множеств была создана Кантором в конце XIX века.

История определения

До XIX века считалось, что точного определения множества нет. Множеством считалось любое скопление предметов.

В конце XIX века Георг Кантор определил множество как «единое имя для совокупности всех объектов, обладающих данным свойством». Эти объекты называются элементами множества. Множество объектов, обладающих свойством A(x), обозначается 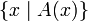$\{x\mid A(x)\}$. Если некое множество 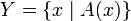$Y=\{x\mid A(x)\}$, то A(x) называется характеристическим свойством множества Y.

Эта концепция привела к парадоксам, в частности, к парадоксу Рассела.

После этого теория множеств была аксиоматизирована.

Аксиоматическая теория множеств

На сегодняшний день множество определяется как модель, удовлетворяющая аксиомам ZFC (аксиомы Цермело — Френкеля с аксиомой выбора). При таком подходе в некоторых математических теориях возникают совокупности объектов, которые не являются множествами. Такие совокупности называются классами (различных порядков).

Элемент множества

Объекты, из которых состоит множество, называют элементами множества или точками множества. Множества чаще всего обозначают большими буквами латинского алфавита, его элементы — маленькими. Если а — элемент множества А, то записывают а ∈ А (а принадлежит А). Если а не является элементом множества А, то записывают а∉А(а не принадлежит А).

Некоторые виды множеств

• Пустое множество
• Упорядоченное множество -- множество, на котором задано отношение порядка.
• Набор (в частности, упорядоченная пара). В отличие от просто множества записывается внутри круглых скобок: (x₁, x₂, x₃, …), а элементы могут повторяться.

По иерархии:

Множество множеств

Подмножество

Надмножество

По ограничению:

Операции над множествами

Основная статья: Операции над множествами

Литература

• Столл Р. Р. Множества. Логика. Аксиоматические теории. — М.: Просвещение, 1968. — 232 с.

См. также

• Круги Эйлера
• Носитель