- РИМАНОВА СВЯЗНОСТЬ
- аффинная связность на римановом пространстве М, относительно к-рой метрич. тензор пространства gij является ковариантно постоянным. Если аффинная связность на Мзадана с помощью матрицы локальных форм связности
.
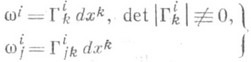 (1)
(1)
и метрич. формой на Мявляется
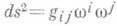 , то последнее условие выражается в виде
, то последнее условие выражается в виде
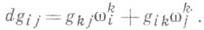 (2)
(2)
Оно может быть выражено еще следующим образом: при параллельном перенесении вдоль любой кривой многообразия Мскалярное произведение

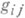
 произвольных двух векторов сохраняет свое значение, т. е. для любых векторных полей X, Y, Z на Мсправедливо равенство
произвольных двух векторов сохраняет свое значение, т. е. для любых векторных полей X, Y, Z на Мсправедливо равенство
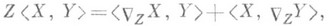
где
 - векторное поле, называемое ковариантной производной поля Xотносительно поля Zи определяемое формулой
- векторное поле, называемое ковариантной производной поля Xотносительно поля Zи определяемое формулой
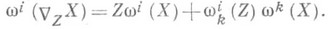
Если на Мперейти к локальному полю ортонормированных реперов, то
 (если ограничиться случаем положительно определенной ds2) и условие (2) принимает вид
(если ограничиться случаем положительно определенной ds2) и условие (2) принимает вид

т. е. матрица w, составленная из форм (1), принимает значения в алгебре Ли группы движений евклидова пространства Е n размерности n=dim М. Поэтому Р. с. может быть интерпретирована как связность в расслоенном пространстве ортонормированных реперов в касательных к Мевклидовых пространствах. Голономии группа Р. с. есть нек-рая подгруппа группы движений пространства Е n;римановой связностью для нек-рой римановой метрики на Мявляется каждая аффинная связность, группа голономии к-рой - группа движений или нек-рая ее подгруппа.
Если в (1) wi - dх i (то есть Мотнесено к полю натуральных реперов локальной координатной системы), то
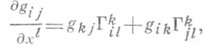
и
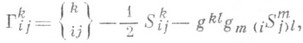
где

- т. н. символ Кристоффеля и
 - тензор кручения Р.. с. Существует одна и только одна Р. с. без кручения (т. е. такая, что
- тензор кручения Р.. с. Существует одна и только одна Р. с. без кручения (т. е. такая, что 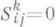 ), к-рая определяется формами
), к-рая определяется формами  и наз. Леви-Чивита связностью.
и наз. Леви-Чивита связностью.
Лит.:[1] Г р о м о л Д., К л и н г е н б е р г В., М е й е р В., Риманова геометрия в целом, пер. с нем., М., 1971; [2] Лихнерович А., Теория связностей в целом и группы голономии, пер. с франц., М., 1960. Ю. Г. Лумисте.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
