ВЕЙЛЯ СВЯЗНОСТЬ

- аффинная связность без кручения на римановом пространстве М, обобщающая Леви-Чивита связность в том смысле, что ковариант-ный дифференциал метрич. тензора 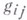пространства Мотносительно нее необязательно, равен нулю, но является пропорциональным самому тензору . Если аффинная связность на Мзадана с помощью 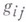матрицы локальных форм связности

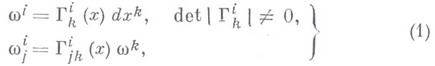
и то она является В. с. <тогда и только тогда, когда

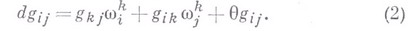
Другая, эквивалентная форма этого условия:

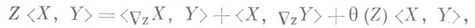
где 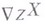- ковариантная производная 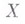по 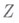- определяется формулой

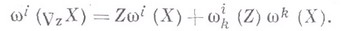
Относительно локального поля ортонормированных реперов, где 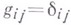, имеет место

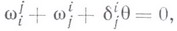
то есть В. с. для нек-рой римановой метрики на Мявляется каждая аффинная связность без, кручения, голономии группа к-рой является группой подобий или нек-рой ее подгруппой.

Если в (1) , то в случае В. с.

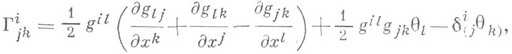
где 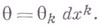Так как

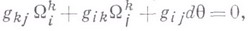
то тензор

наз. (по Вейлю) тензором кривизны направлений, антисимметричен по обеим парам индексов:

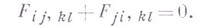
В. с. введена Г. Вейлем [1].

Лит.:[llWeyl Н., "Math. Z.", 1918, Bd 2, S. 384-411; [2] Норден А. П., Пространства аффинной связности, М.-Л., 1950; [3] Fо11and G. В., "J. Different. Geom.", 1970, v. 4, p. 145 - 53. Ю. Г. .Лумисте.