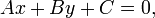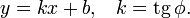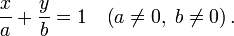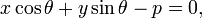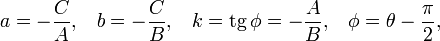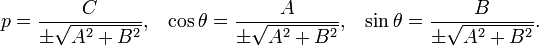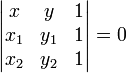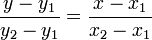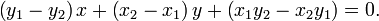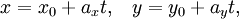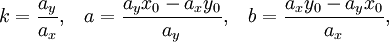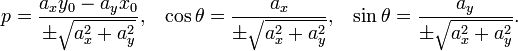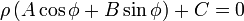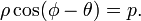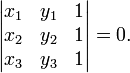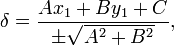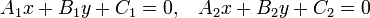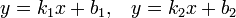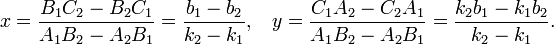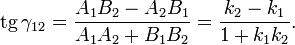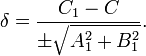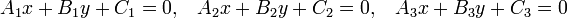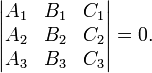Прямые

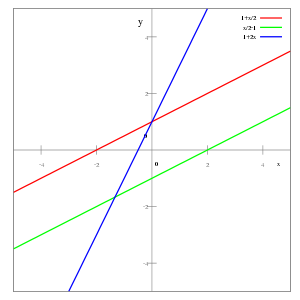Изображение прямых в прямоугольной системе координат

Прямая — одно из основных понятий геометрии.

При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.

Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.

Аналитически прямая задаётся уравнением (в трёхмерном пространстве — системой уравнений) первой степени.

Свойства прямой в евклидовой геометрии

• Через любые две несовпадающие точки можно провести единственную прямую.
• Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются параллельными.
• В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:
  • прямые пересекаются;
  • прямые параллельны;
  • прямые скрещиваются.
• Прямая линия — алгебраическая линия первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение).

Уравнения прямой на плоскости

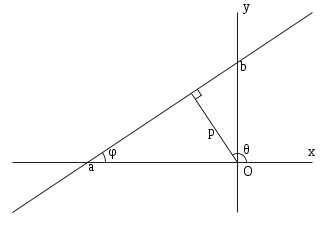Способы задания прямой:
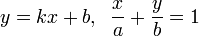$y=kx+b,\;\;\frac{x}{a}+\frac{y}{b}=1\,$ или $x\cos\theta+y\sin\theta-p=0\,$

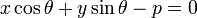
Общее уравнение прямой линии на плоскости в декартовых координатах:

$Ax+By+C=0,\,$

где A и B одновременно не равны нулю. При C = 0 прямая проходит через начало координат.

Уравнение прямой с угловым коэффициентом. Прямая линия, пересекающая ось Oy в точке 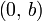$\left(0,\,b\right)$ и образующая угол φ с положительным направлением оси Ox:

$y=kx+b,\;\;\;k=\operatorname{tg}\,\phi.$

Коэффициент k называется угловым коэффициентом прямой. В этом виде невозможно представить прямую, параллельную оси Oy.

Уравнение прямой в отрезках. Прямая линия, пересекающая ось Ox в точке 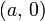$\left(a,\,0\right)$ и ось Oy в точке $\left(0,\,b\right)$:

$\frac{x}{a}+\frac{y}{b}=1\;\;\;\left(a\ne0,\;b\ne0\right).$

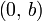В этом виде невозможно представить прямую, проходящую через начало координат.

Нормальное уравнение прямой:

$x\cos\theta+y\sin\theta-p=0,\,$

где p — длина перепендикуляра, опущенного на прямую из начала координат, а θ — угол (измеренный в положительном направлении) между положительным направлением оси Ox и направлением этого перпендикуляра. Если p = 0, то прямая проходит через начало координат, а угол 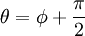$\theta=\phi+\frac{\pi}{2}$ задаёт угол наклона прямой.

Если прямая задана общим уравнением Ax + By + C = 0, то отрезки a и b, отсекаемые ею на осях, угловой коэффициент k, расстояние прямой от начала координат p, cosθ и sinθ выражаются через коэффициенты A, B и C следующим образом:

$a=-\frac{C}{A},\;\;\;b=-\frac{C}{B},\;\;\;k=\operatorname{tg}\,\phi=-\frac{A}{B},\;\;\;\phi=\theta-\frac{\pi}{2},$

$p=\frac{C}{\pm\sqrt{A^2+B^2}},\;\;\;\cos\theta=\frac{A}{\pm\sqrt{A^2+B^2}},\;\;\;\sin\theta=\frac{B}{\pm\sqrt{A^2+B^2}}.$

Во избежание неопределённости знак перед радикалом выбирается так, чтобы соблюдалось условие p > 0. В этом случае cosθ и sinθ являются направляющими косинусами положительной нормали прямой — перпендикуляра, опущенного из начала координат на прямую. Если C = 0, то прямая проходит через начало координат и выбор положительного напрвления произволен.

Уравнение прямой, проходящей через две заданные несовподающие точки $\left(x_1,y_1\right)$ и $\left(x_2,y_2\right)$

$\begin{vmatrix} x & y & 1 \\ x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \end{vmatrix} = 0$

или

$\frac{y-y_1}{y_2-y_1}=\frac{x-x_1}{x_2-x_1}$

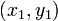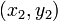
или в общем виде

$\left(y_1-y_2\right)x + \left(x_2 - x_1\right)y + \left(x_1y_2 - x_2y_1\right) = 0.$

Параметрические уравнения прямой могут быть записаны в виде:

$x = x_0 + a_xt,\;\;\;y = y_0 + a_yt,$

где t — производный параметр, при этом

$k = \frac{a_y}{a_x},\;\;\;a=\frac{a_yx_0 - a_xy_0}{a_y},\;\;\;b=\frac{a_xy_0 - a_yx_0}{a_x},$

$p=\frac{a_xy_0 - a_yx_0}{\pm\sqrt{a_x^2 + a_y^2}},\;\;\;\cos\theta=\frac{a_x}{\pm\sqrt{a_x^2 + a_y^2}},\;\;\;\sin\theta=\frac{a_y}{\pm\sqrt{a_x^2 + a_y^2}}.$

Уравнение прямой в полярных координатах ρ и φ:

$\rho\left(A\cos\phi + B\sin\phi\right) + C = 0$

или

$\rho\cos(\phi-\theta)=p.\,$

Тангенциальное уравнение прямой на плоскости:

ξx + ηy = 1

Числа ξ и η называются её тангенциальными, линейными или плюккеровыми координатами.

Уравнения прямой в пространстве

Каноническое уравнение прямой в пространстве:

Пусть M(x₀,y₀,z₀) — точка, лежащая на прямой, и 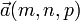$\vec a(m, n, p)$ — вектор, ей коллинеарный. Тогда уравнение прямой имеет вид: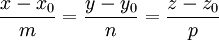 $\frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p}$

Взаимное расположение точек и прямых

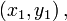
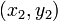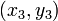Три точки $\left(x_1,y_1\right),$ $\left(x_2,y_2\right)$ и $\left(x_3,y_3\right)$ лежат на одной прямой тогда и только тогда, если выполняется условие

$\begin{vmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{vmatrix} = 0.$

Отклонение точки 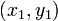$\left(x_1,y_1\right)$ от прямой Ax + By + C = 0 может быть найдено по формуле

$\delta = \frac{Ax_1 + By_1 + C}{\pm\sqrt{A^2+B^2}},$

где знак перед радикалом противоположен знаку C. Отклонение по модулю равно расстоянию между точкой и прямой; оно положительно, если точка и начало координат лежат по разные стороны от прямой, и отрицательно, если по одну сторону.

Взаимное расположение нескольких прямых

Две прямые, заданные уравнениями

$A_1x+B_1y+C_1=0,\;\;\;A_2x+B_2y+C_2=0$

или

$y=k_1x+b_1,\;\;\;y=k_2x+b_2$

пересекаются в точке

$x=\frac{B_1C_2-B_2C_1}{A_1B_2-A_2B_1}=\frac{b_1-b_2}{k_2-k_1},\;\;\;y=\frac{C_1A_2-C_2A_1}{A_1B_2-A_2B_1}=\frac{k_2b_1-k_1b_2}{k_2-k_1}.$

Угол γ₁₂ между пересекающимися прямыми определяется формулой

$\operatorname{tg}\,\gamma_{12}=\frac{A_1B_2-A_2B_1}{A_1A_2+B_1B_2}=\frac{k_2-k_1}{1+k_1k_2}.$

При этом под γ₁₂ понимается угол, на который надо повернуть первую прямую (заданную параметрамиA₁, B₁, C₁, k₁ и b₁) вокруг точки пересечения против часовой стрелки до первого совмещения со второй прямой.

Эти прямые параллельны, если A₁B₂ − A₂B₁ = 0 или k₁ = k₂, и перпендикулярны, если A₁A₂ + B₁B₂ = 0 или $k_1=-\frac{1}{k_2}.$

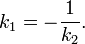
Любую прямую, паралельную A₁x + B₁y + C₁ = 0, можно выразить уравнением A₁x + B₁y + C = 0. При этом расстояние между ними будет равно

$\delta = \frac{C_1-C}{\pm\sqrt{A_1^2+B_1^2}}.$

Если знак перед радикалом противоположен C₁, то δ будет положительным, когда вторая прямая и начало координат лежат по разные стороны от первой прямой.

Для того, чтобы три прямые

$A_1x+B_1y+C_1=0,\;\;\;A_2x+B_2y+C_2=0,\;\;\;A_3x+B_3y+C_3=0$

пересекались в одной точке или были параллельны друг другу, необходимо и достаточно, чтобы выполнялось условие

$\begin{vmatrix} A_1 & B_1 & C_1 \\ A_2 & B_2 & C_2 \\ A_3 & B_3 & C_3 \end{vmatrix} = 0.$

См. также

• Геодезическая

Ссылки

• Математическая энциклопедия (в 5-и томах), Москва, «Советская Энциклопедия», 1982 г.
• Маркушевич А. И. Замечательные кривые, Популярные лекции по математике, выпуск 4, Гостехиздат 1952 г., 32 стр.