Параллельные прямые

Параллельные прямые

В Евклидовой геометрии

Параллельными (иногда — равнобежными) прямыми называются прямые, которые лежат в одной плоскости и либо совпадают, либо не пересекаются. В некоторых школьных определениях совпадающие прямые не считаются параллельными, здесь такое определение не рассматривается.

Свойства

1. Параллельность — бинарное отношение эквивалентности, поэтому разбивает всё множество прямых на классы параллельных между собой прямых.
2. Через любую точку можно провести ровно одну прямую, параллельную данной. Это отличительное свойство евклидовой геометрии, в других геометриях число 1 заменено другими (в геометрии Лобачевского таких прямых минимум две)
3. 2 параллельные прямые в пространстве лежат в одной плоскости.
4. При пересечении 2 параллельных прямых третьей, называемой секущей:
   1. Секущая обязательно пересекает обе прямые.
   2. При пересечении образуется 8 углов, некоторые характерные пары которых имеют особые названия и свойства:
      1. Накрест лежащие углы равны.
      2. Соответственные углы равны.
      3. Односторонние углы в сумме составляют 180°.

В геометрии Лобачевского

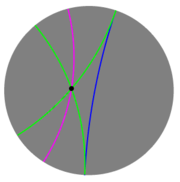Параллельные прямые в модели Пуанкаре: две зелёные прямые параллельны синей прямой, а фиолетовая ультрапараллельна к ней

В геометрии Лобачевского в плоскости через точку Невозможно разобрать выражение (лексическая ошибка): C</math¹> вне данной прямой <math>AB

проходит бесконечное множество прямых, не пересекающих AB. Из них параллельными к AB называются только две.

Прямая CE называется равнобежной (параллельной) прямой AB в направлении от A к B, если:

1. точки B и E лежат по одну сторону от прямой AC;
2. прямая CE не пересекает прямую AB, но всякий луч, проходящий внутри угла ACE, пересекает луч AB.

Аналогично определяется прямая, равнобежная AB в направлении от B к A.

Все остальные прямые, не пересекающие данную, называются ультрапараллельными или расходящимися.

См. также

• Скрещивающиеся прямые
• Перпендикулярность
• Ортогональность