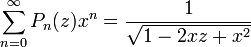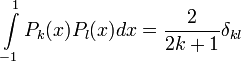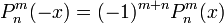Присоединённые многочлены Лежандра
- Присоединённые многочлены Лежандра
-
Многочлены Лежандра — определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов 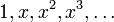 ортогонализацией Грама ― Шмидта.
ортогонализацией Грама ― Шмидта.
Названы по имени французского математика Адриен Мари Лежандра.
Определение
Многочлены Лежандра определяются по формуле (называемой формулой Родрига)
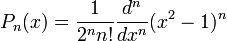
часто записываемой в виде
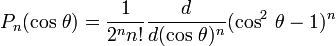
Они также могут быть вычислены по рекуррентной формуле
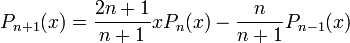
Присоединённые многочлены Лежандра определяются по формуле
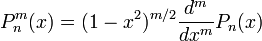
которую также можно представить в виде
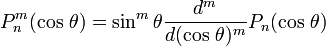
При m = 0 функция 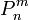 совпадает с Pn.
совпадает с Pn.
Примеры
Первые четыре многочлена Лежандра равны:
- P0(x) = 1
- P1(x) = x
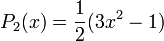
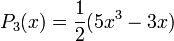
Свойства
![{d \over dx} \left[ (1-x^2) {d \over dx} P_n(x) \right] - \frac{m^2}{(1-x^2)} P_n(x) + n(n+1)P_n(x) = 0.](/pictures/wiki/files/57/9737be98642c29101417b8021fd720c1.png)
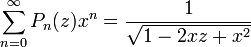
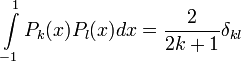
- При каждом m > 0 система присоединённых функций Лежандра
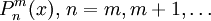 полна в L2( − 1,1).
полна в L2( − 1,1).
- В зависимости от m и n присоединённые многочлены Лежандра могут быть как чётными, так и нечётными функциями:
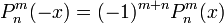
Функции Лежандра
-
Многочлены Лежандра (вместе с присоединёнными функциями Лежандра Pn,m(x)) естественно возникают в теории потенциала. Сферические функции — это функции (в сферических координатах r,θ,φ) вида
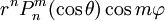 и
и 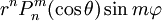 ,
,
где 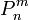 — присоединённые многочлены Лежандра. Сферические функции удовлетворяют уравнению Лапласа всюду в
— присоединённые многочлены Лежандра. Сферические функции удовлетворяют уравнению Лапласа всюду в 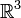 (при n < 0 — всюду, кроме нуля) и служат ортогональным базисом для функций.
(при n < 0 — всюду, кроме нуля) и служат ортогональным базисом для функций.
Литература
- В.С. Владимиров, В.В. Жаринов. Уравнения математической физики. — М.: Физматлит, 2004. — ISBN 5-9221-0310-5
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Присоединённые многочлены Лежандра" в других словарях:
Многочлены Лежандра — Многочлен Лежандра многочлен, который в наименьшей степени отклоняется от нуля в смысле среднего квадратического. Образует ортогональную систему многочленов, на отрезке по мере Лебега. Многочлены Лежандра могут быть получены из многочленов… … Википедия
Многочлен Лежандра — Многочлены Лежандра определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта. Названы по имени французского математика Адриен Мари… … Википедия
Полином Лежандра — Многочлены Лежандра определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта. Названы по имени французского математика Адриен Мари… … Википедия
Полиномы Лежандра — Многочлены Лежандра определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта. Названы по имени французского математика Адриен Мари… … Википедия
Функция Лежандра — Многочлены Лежандра определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта. Названы по имени французского математика Адриен Мари… … Википедия
C++ Technical Report 1 — (TR1) является общим названием для стандарта ISO / IEC TR 19768, библиотеки расширений C++ это документ с предложением дополнений в стандарт библиотеки С++. Дополнения включают регулярные выражения, умные указатели, хэш таблицы, и… … Википедия
Сферические функции — представляют собой угловую часть семейства ортогональных решений уравнения Лапласа, записанную в сферических координатах. Они широко используются для изучения физических явлений в пространственных областях, ограниченных сферическими поверхностями … Википедия
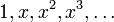 ортогонализацией Грама ― Шмидта.
ортогонализацией Грама ― Шмидта.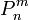 совпадает с Pn.
совпадает с Pn.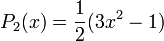
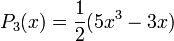
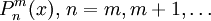 полна в L2( − 1,1).
полна в L2( − 1,1).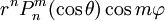 и
и 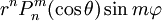 ,
,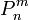 — присоединённые многочлены Лежандра. Сферические функции удовлетворяют уравнению Лапласа всюду в
— присоединённые многочлены Лежандра. Сферические функции удовлетворяют уравнению Лапласа всюду в 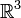 (при n < 0 — всюду, кроме нуля) и служат ортогональным базисом для функций.
(при n < 0 — всюду, кроме нуля) и служат ортогональным базисом для функций.
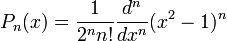
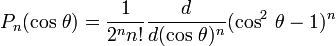
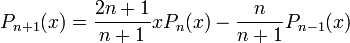
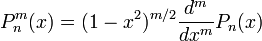
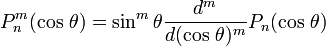
![{d \over dx} \left[ (1-x^2) {d \over dx} P_n(x) \right] - \frac{m^2}{(1-x^2)} P_n(x) + n(n+1)P_n(x) = 0.](/pictures/wiki/files/57/9737be98642c29101417b8021fd720c1.png)