Прикосновения точка

В геометрии и топологии замыка́ние подмножества топологического пространства — это пересечение всех замкнутых подмножеств содержащих данное подмножество. Эквивалентно, замыкание подмножества — это совокупность всех его точек прикосновения.

Точка прикосновения

Определение

Пусть задано топологическое пространство 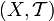$(X,\mathcal{T})$, и подмножество 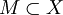$M \subset X$. Точка $x \in X$ называется то́чкой прикоснове́ния множества M, если любая её окрестность пересекается с M. То есть,

$\forall U \in \mathcal{T}\quad ( x \in U ) \Rightarrow (U \cap M \not= \emptyset).$

Замечание

Очевидно, если 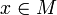$x\in M$, то x является точкой прикосновения. Обратное, вообще говоря, неверно.

Примеры

Пусть 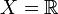$X = \mathbb{R}$ - множество действительных чисел со стандартной топологией, и M = (a,b) - произвольный интервал. Тогда любая точка $x\in [a,b]$ является точкой прикосновения M.

Замыкание

Определение

Совокупность всех точек прикосновения множества 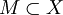$M \subset X$ называется замыканием множества M и обозначается $\bar{M}$ или cl(M).

Свойства

1. Операция замыкания является унарной операцией на множестве всех подмножеств X.
2. Замыкание множества содержит само множество, то есть $M \subset \bar{M}$.
3. Замыкание множества замкнуто.
4. Множество замкнуто тогда и только тогда, когда оно совпадает со своим замыканием, то есть $M = \bar{M}$.
5. В частности, $\bar{X} = X,\; \bar{\emptyset} = \emptyset.$
6. $\bar{\bar{M}} = \bar{M}.$
7. Замыкание множества M является наименьшим замкнутым множеством, содержащим M, то есть $\bar{M} = \bigcap \left\{C \supset M \mid C = \bar{C}\right\}.$
8. Замыкание сохраняет отношение вложения, то есть $(M \subset N) \Rightarrow \left( \bar{M} \subset \bar{N} \right).$
9. Замыкание объединения есть объединение замыканий, то есть $\overline{A \cup B} = \bar{A} \cup \bar{B}.$
10. Замыкание пересечения есть подмножество пересечения замыканий (но, вообще говоря, не равно ему), то есть $\overline{A \cap B} \subset \bar{A} \cap \bar{B}.$

Замечание

Свойство 7 часто принимается в качестве определения замыкания. Данное выше определение тогда выводится в качестве одного из свойств.

Примеры

Во всех нижеследующих примерах топологическим пространство является числовая прямая $\mathbb{R}$ с заданной на ней стандартной топологией.

• $\overline{(a,b)} = [a,b]$;
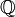• $\bar{\mathbb{Q}} = \mathbb{R}$, где $\mathbb{Q}$ - множество рациональных чисел.