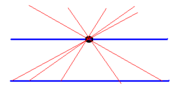
Постулат Евклида о параллельных

Пересечения прямых (анимация)

Аксио́ма паралле́льности Евкли́да, или пя́тый постула́т — одна из аксиом, лежащих в основании классической планиметрии. Впервые приведена в «Началах» Евклида ^[1]:

И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то продолженные неограниченно эти прямые встретятся с той стороны, где углы меньше двух прямых. Оригинальный текст (др.-греч.)   Καὶ ἐὰν εἰς δύο εὐθείας εὐθεῖα ἐμπίπτουσα τὰς ἐντὸς καὶ ἐπὶ τὰ αὐτὰ μέρη γωνίας δύο ὀρθῶν ἐλάσσονας ποιῇ, ἐκβαλλομένας τὰς δύο εὐθείας ἐπ' ἄπειρον συμπίπτειν, ἐφ' ἃ μέρη εἰσὶν αἱ τῶν δύο ὀρθῶν ἐλάσσονες. — ΣTOIXEIA EΥKΛEI∆OΥ

Евклид различает понятия постулат и аксиома, не объясняя их различия; в разных манускриптах «Начал» Евклида разбиение утверждений на аксиомы и постулаты различно, равно как не совпадает и их порядок. В классическом издании «Начал» Гейберга сформулированное утверждение является пятым постулатом.

На современном языке текст Евклида можно переформулировать так:

Если сумма внутренних углов с общей стороной, образованных двумя прямыми при пересечении их третьей, с одной из сторон от секущей меньше 180°, то эти прямые пересекаются, и притом по ту же сторону от секущей.

Эквивалентные формулировки

В школьных учебниках обычно приводится другая формулировка, эквивалентная (равносильная) V постулату и принадлежащая Проклу ^[2]:

Постулат Прокла

В плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.

Вообще у V постулата имеется огромное количество эквивалентных формулировок, многие из которых кажутся довольно очевидными. Вот некоторые из них ^[3]:

• Существует прямоугольник (хотя бы один), то есть четырёхугольник, у которого все углы прямые.
• Существуют подобные, но не равные треугольники.
• Любую фигуру можно пропорционально увеличить.
• Существует треугольник сколь угодно большой площади.
• Через каждую точку внутри острого угла всегда можно провести прямую, пересекающую обе его стороны.
• Если две прямые в одну сторону расходятся, то в другую — сближаются.
• Сближающиеся прямые рано или поздно пересекутся.
• Существуют такие прямые, что расстояние от точек одной до другой постоянно.
• Если две прямые начали сближаться, то невозможно, чтобы они затем начали (в ту же сторону, без пересечения) расходиться.
• Сумма углов одинакова у всех треугольников.
• Существует треугольник, сумма углов которого равна двум прямым.
• Существуют параллельные прямые, причём две прямые, параллельные третьей, параллельны и друг другу.
• Существуют параллельные прямые, причём прямая, пересекающая одну из параллельных прямых, непременно пересечёт и другую.
• Для всякого невырожденного треугольника существует описанная окружность.
  • Вариант: через любые три точки можно провести либо прямую, либо окружность.
• Справедлива теорема Пифагора.

Эквивалентность их означает, что все они могут быть доказаны, если принять V постулат, и наоборот, заменив V постулат на любое из этих утверждений, мы сможем доказать исходный V постулат как теорему.

Если из списка аксиом исключить V постулат, то полученная система аксиом будет описывать так называемую абсолютную геометрию.

Если вместо V постулата допустить, что для пары точка—прямая V постулат неверен, то полученная система аксиом будет описывать геометрию Лобачевского. Понятно, что в геометрии Лобачевского все вышеперечисленные эквивалентные утверждения неверны.

Система аксиом сферической геометрии требует изменения также и других аксиом Евклида.

Попытки доказательства

Пятый постулат резко выделяется среди других, вполне очевидных (см. Начала Евклида). Он больше похож на сложную, неочевидную теорему. Евклид, вероятно, сознавал это, и поэтому первые 28 предложений в «Началах» доказываются без его помощи.

Математики с давних времён пытались «улучшить Евклида» — либо исключить пятый постулат из числа исходных утверждений, то есть доказать его, опираясь на остальные постулаты и аксиомы, либо заменить его другим, столь же очевидным, как другие постулаты. Надежду на достижимость этого результата поддерживало то, что IV постулат Евклида (все прямые углы равны) действительно оказался лишним — он был строго доказан как теорема и исключён из перечня аксиом.

За два тысячелетия было предложено много доказательств пятого постулата, но в каждом из них рано или поздно обнаруживался порочный круг: оказывалось, что среди явных или неявных посылок содержится утверждение, которое не удаётся доказать без использования того же пятого постулата.

Прокл (V век н. э.) в «Комментарии к I книге Начал Евклида» сообщает, что такое доказательство предложил Клавдий Птолемей, критикует его доказательство и предлагает своё собственное, опираясь на допущение, что расстояние между двумя непересекающимися прямыми есть ограниченная величина. Впоследствии выяснилось, что это допущение равносильно V постулату.

После упадка античной культуры V постулатом занялись математики стран ислама. Доказательство ал-Джаухари, ученика ал-Хорезми (IX век) ^[4], неявно подразумевало: если при пересечении двух прямых какой-либо третьей накрест-лежащие углы равны, то то же имеет место при пересечении тех же двух прямых любой другой. И это допущение равносильно V постулату.

Сабит ибн Курра (IX век) дал два доказательства; в первом он опирается на предположение, что если две прямые удаляются друг от друга с одной стороны, они обязательно приближаются с другой стороны. Во втором — исходит из существования равноотстоящих прямых, причём этот факт ибн Курра пытается вывести из представления о «простом движении», т. е. о равномерном движении на фиксированном расстоянии от прямой (ему представляется очевидным, что траектория такого движения — тоже прямая) ^[5]. Каждое из двух упомянутых утверждений Ибн Курры эквивалентно V постулату.

Четырёхугольник Ламберта

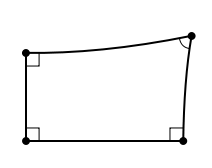
Аналогичную ошибку сделал ибн ал-Хайсам, но он впервые рассмотрел фигуру, позже получившую название «четырёхугольник Ламберта» — четырёхугольник, у которого три внутренних угла — прямые. Он сформулировал три возможных варианта для четвёртого угла: острый, прямой, тупой. Обсуждение этих трёх гипотез, в разных вариантах, многократно возникало в позднейших исследованиях.

Поэт и математик Омар Хайям подверг критике попытки ввести в геометрию механическое движение. Он предложил заменить V постулат на другой, более простой: две сходящиеся прямые пересекаются, и невозможно, чтобы две сходящиеся прямые расходились в направлении схождения. Каждая из двух частей этого утверждения равносильна постулату Евклида ^[6].

Ал-Абхари предложил доказательство, сходное с доказательством ал-Джаухари. (Это доказательство приводит в своей книге ас-Самарканди, и ряд исследователей считал его доказательством ас-Самарканди.) Он исходит из верного в абсолютной геометрии утверждения о том, что для всякой прямой, пересекающей стороны данного угла, может быть построена ещё одна прямая, пересекающая стороны этого же угла и отстоящая от его вершины дальше, чем первая. Но из этого утверждения он делает логически необоснованный вывод о том, что через всякую точку внутри данного угла можно провести прямую, пересекающую обе стороны этого угла, — и основывает на этом последнем утверждении, эквивалентном V постулату, всё дальнейшее доказательство.

Насир ад-Дин ат-Туси предложил построение, аналогичное построению Омара Хайяма ^[7]. Отметим, что сочинения ат-Туси стали известны Джону Валлису, и тем самым сыграли роль в развёртывании исследований по неевклидовой геометрии в Европе.

Первую в Европе известную нам попытку доказательства аксиомы параллельности Евклида предложил живший в Провансе (Франция) Герсонид (он же Леви бен Гершом, XIV век). Его доказательство опиралось на утверждение о существовании прямоугольника ^[8].

К XVI веку относится доказательство учёного-иезуита Христофора Клавиуса. Доказательство его, как и у ибн Курры, основывалось на утверждении, что линия, равноотстоящая от прямой — тоже прямая ^[9].

Валлис в 1693 году в одной из своих работ воспроизводит перевод сочинения ат-Туси и предлагает эквивалентную, но более простую формулировку: существуют подобные, но не равные фигуры ^[10]. Клеро в своих «Началах геометрии» (1741), как и Герсонид, вместо V постулата взял его эквивалент «существует прямоугольник».

В целом можно сказать, что все перечисленные попытки принесли немалую пользу: была установлена связь между V постулатом и другими утверждениями, были отчётливо сформулированы две альтернативы V постулату — гипотезы острого и тупого угла.

Первые наброски неевклидовой геометрии

Сочинение Саккери

Глубокое исследование V постулата, основанное на совершенно оригинальном принципе, провёл в 1733 году итальянский монах-иезуит, преподаватель математики Джироламо Саккери. Он опубликовал труд под названием «Евклид, очищенный от всех пятен, или же геометрическая попытка установить самые первые начала всей геометрии». Идея Саккери состояла в том, чтобы заменить V постулат противоположным утверждением, вывести из новой системы аксиом как можно больше следствий, тем самым построив «ложную геометрию», и найти в этой геометрии противоречия или заведомо неприемлемые положения. Тогда справедливость V постулата будет доказана от противного ^[11].

Саккери рассматривает всё те же три гипотезы о 4-м угле четырёхугольника Ламберта. Гипотезу тупого угла он отверг сразу по формальным соображениям. Легко показать, что в этом случае вообще все прямые пересекаются, а тогда можно заключить, что V постулат Евклида справедлив — ведь он как раз и утверждает, что при некоторых условиях прямые пересекаются. Отсюда делается вывод, что «гипотеза тупого угла всегда целиком ложна, так как она сама себя разрушает» ^[12].

После этого Саккери переходит к опровержению «гипотезы острого угла», и здесь его исследование гораздо интереснее. Он допускает, что она верна, и, одно за другим, доказывает целый ряд следствий. Сам того не подозревая, он продвигается довольно далеко в построении геометрии Лобачевского. Многие теоремы, доказанные Саккери, выглядят интуитивно неприемлемыми, но он продолжает цепочку теорем. Наконец, Саккери доказывает, что в «ложной геометрии» любые две прямые или пересекаются, или имеют общий перпендикуляр, по обе стороны от которого они удаляются друг от друга, или же удаляются друг от друга с одной стороны и неограниченно сближаются с другой. В этом месте Саккери делает неожиданный вывод: «гипотеза острого угла совершенно ложна, так как противоречит природе прямой линии» ^[13].

Видимо, Саккери чувствовал необоснованность этого «доказательства», потому что исследование продолжается. Он рассматривает эквидистанту — геометрическое место точек плоскости, равноотстоящих от прямой; в отличие от своих предшественников, Саккери знает, что в рассматриваемом случае это вовсе не прямая. Однако, вычисляя длину её дуги, Саккери допускает ошибку и приходит к реальному противоречию, после чего заканчивает исследование и с облегчением заявляет, что он «вырвал эту зловредную гипотезу с корнем».

Во второй половине XVIII века было опубликовано более 50 работ по теории параллельных. В обзоре тех лет (Г. С. Клюгель) исследуется более 30 попыток доказать V постулат и доказывается их ошибочность. Известный немецкий математик и физик И. Г. Ламберт, с которым Клюгель переписывался, тоже заинтересовался проблемой; его «Теория параллельных линий» была издана посмертно в 1786 году.

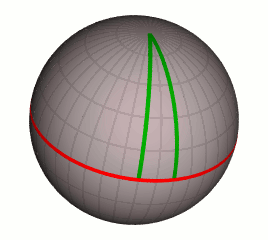
Сферическая геометрия: все прямые пересекаются

Ламберт первым обнаружил, что «геометрия тупого угла» реализуется на сфере, если под прямыми понимать большие круги. Он, как и Саккери, вывел из «гипотезы острого угла» множество следствий, причём продвинулся гораздо дальше Саккери; в частности, он обнаружил, что дополнение суммы углов треугольника до 180° пропорционально площади треугольника.

В своей книге Ламберт проницательно отметил ^[14]:

Мне кажется очень замечательным, что вторая гипотеза [тупого угла] оправдывается, если вместо плоских треугольников взять сферические. Я из этого почти должен был бы сделать вывод — заключение, что третья гипотеза имеет место на какой-то мнимой сфере. Во всяком случае, должна же существовать причина, почему она на плоскости далеко не так легко поддаётся опровержению, как это могло быть сделано в отношении второй гипотезы.

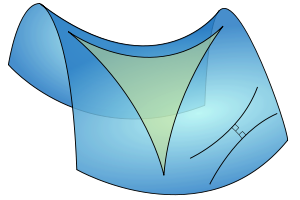
Геометрия на поверхности отрицательной кривизны

Ламберт не нашёл противоречия в гипотезе острого угла и пришёл к заключению, что все попытки доказать V постулат безнадёжны. Однако в ложности «геометрии острого угла» он не сомневался.

Тем временем попытки «смыть пятна» с Евклида продолжались (Луи Бертран, Лежандр и другие). Лежандр дал целых три доказательства V постулата, ошибочность которых быстро показали его современники ^[15]. Последнее «доказательство» он опубликовал в 1823 году, за три года до первого доклада Лобачевского о новой геометрии.

Открытие неевклидовой геометрии

В первой половине XIX века по пути, проложенному Саккери, пошли сразу три математика: К. Ф. Гаусс, Н. И. Лобачевский и Я. Бойяи. Но цель у них была уже иная — не разоблачить неевклидову геометрию как невозможную, а, наоборот, построить альтернативную геометрию и выяснить её возможную роль в реальном мире. На тот момент это была совершенно еретическая идея; никто из учёных ранее не сомневался, что физическое пространство евклидово. Интересно, что Гаусса и Лобачевского учил в молодости один и тот же учитель — Мартин Бартельс.

Первым был Гаусс. Он не публиковал никаких работ на эту тему, но его черновые заметки и несколько писем однозначно подтверждают его понимание неевклидовой геометрии. В 1818 году в письме к австрийскому астроному Герлингу он писал ^[16]:

Я радуюсь, что вы имеете мужество высказаться так, как если бы Вы признавали ложность нашей теории параллельных, а вместе с тем и всей нашей геометрии. Но осы, гнездо которых Вы потревожите, полетят Вам на голову.

Ознакомившись с работой Лобачевского «Геометрические исследования по теории параллельных», Гаусс энергично ходатайствует об избрании русского математика иностранным членом-корреспондентом Гёттингенского королевского общества (что и произошло в 1842 году).

Евклид

Н. И. Лобачевский

Лобачевский и Бойяи проявили бо́льшую смелость, чем Гаусс, и почти одновременно (около 1830 года), независимо друг от друга, опубликовали изложение того, что сейчас называется геометрией Лобачевского. Лобачевский продвинулся в исследовании новой геометрии дальше всех, и она в настоящий момент носит его имя. Но главная его заслуга не в этом, а в том, что он поверил в новую геометрию и имел мужество отстаивать своё убеждение (он даже предложил экспериментально проверить V постулат, измерив сумму углов треугольника) ^[17].

Трагическая судьба Лобачевского, подвергнутого остракизму в научном мире и служебном окружении за слишком смелые мысли, показала, что опасения Гаусса были не напрасны. Но и его борьба была не напрасна. Спустя несколько десятилетий математики (Бернхард Риман), а затем и физики (Общая теория относительности, Эйнштейн), окончательно покончили с догматом об евклидовой геометрии физического пространства.

Доказать непротиворечивость новой геометрии ни Лобачевский, ни Бойяи не сумели — тогда математика ещё не располагала необходимыми для этого средствами. Только спустя 40 лет появились модель Клейна и другие модели, реализующие аксиоматику геометрии Лобачевского на базе евклидовой геометрии. Эти модели убедительно доказывают, что отрицание V постулата не противоречит остальным аксиомам геометрии; отсюда вытекает, что V постулат независим от остальных аксиом и доказать его невозможно.

Примечания

1. ↑ Начала Евклида / Перевод с греческого и комментарии Д. Д. Мордухай-Болтовского при редакционном участии М. Я. Выгодского и И. Н. Веселовского. — М.-Л.: ГТТИ, 1948. — Т. I. — С. 15.
2. ↑ История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — С. 110.
3. ↑ Euclid’s Fifth Postulate
4. ↑ История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — С. 231.
5. ↑ Ибн Корра. Книга о том, что две линии, проведённые под углом, меньшим двух прямых, встречаются / Перевод и примечания Б. А. Розенфельда. — М.: ИМИ, 1963. — Т. XV. — С. 363—380.
6. ↑ Хаййам. Трактаты / Перевод Б. А. Розенфельда. Редакция В. С. Сегаля и А. П. Юшкевича. Статья и комментарии Б. А. Розенфельда и А. П. Юшкевича. — М.: 1962.
7. ↑ Ат-Туси. Трактат, исцеляющий сомнение по поводу параллельных линий / Перевод Б. А. Розенфельда, примечания Б. А. Розенфельда и А. П. Юшкевича. — М.: ИМИ, 1960. — Т. XIII. — С. 483—532.
8. ↑ Розенфельд Б. А. Доказательства пятого постулата Евклида средневековых математиков Хасана ибн ал-Хайсама и Льва Герсонида. — М.: ИМИ, 1958. — Т. XI. — С. 733—742.
9. ↑ Clavius C. Euclidis Elementorum, libri XV. — Romae: 1574.
10. ↑ Wallis. Opera mathematica, v. II. — Oxoniae: 1693. — С. 665.
11. ↑ История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III. — С. 215-217.
12. ↑ G. Saccheri. Euklid von jedem Makel befreit. In: F. Engel, P. Stackel. Die Theorie der Parallellinien von Euklid bis auf Gauss, eine Urkundensammlung zur Vorgeschichte der Nicht-Euklidischen Geometrie. — Leipzig: 1895. — С. 100.
13. ↑ G. Saccheri. Euklid von jedem Makel befreit. In: F. Engel, P. Stackel. Die Theorie der Parallellinien von Euklid bis auf Gauss, eine Urkundensammlung zur Vorgeschichte der Nicht-Euklidischen Geometrie. — Leipzig: 1895. — С. 105.
14. ↑ Lambert J. H. Deutscher Gelehrter Briefwechsel. Bd. 1-5. Herausg. von J. Bernoulli. — Berlin: 1781—1784. — С. 202—203.
15. ↑ История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III. — С. 218.
16. ↑ Об основаниях геометрии. Сборник классических работ по геометрии Лобачевского и развитию её идей. — М.: ГИТТЛ, 1956. — С. 119-120.
17. ↑ Лобачевский Н. И. Сочинения по геометрии (Полн. собр. соч., тт. 1—3). — М. — Л.: ГИТТЛ, 1946—1949.

Литература

• Вилейтнер Г. История математики от Декарта до середины XIX столетия. ГИФМЛ, 1960. 468 с.
• Гильберт Д. Основания геометрии. — Л., «Сеятель», 1923. 152 с.
• «Начала» Евклида
• История математики с древнейших времён до начала XIX столетия (под ред. А. П. Юшкевича), тома I—III, М., Наука, 1972.
• Каган В. Ф. Геометрия Лобачевского и её предыстория. М.—Л., 1949. (Основания геометрии, ч. 1).
• Розенфельд Б. А. История неевклидовой геометрии: Развитие понятия о геометрическом пространстве. М.: Наука, 1976.
• Розенфельд Б. А., Юшкевич А. П. Теория параллельных линий на средневековом Востоке. М.: Наука, 1983.
• Смилга В. П. В погоне за красотой. Занимательное введение в неевклидову геометрию. М., 1968 (серия «Эврика»).
• Об основаниях геометрии. Сборник классических работ по геометрии Лобачевского и развитию её идей. М., 1956.

Ссылки

• Пятый постулат Евклида