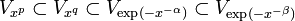- Отрицательная вариация
-
В математическом анализе вариацией функции называется числовая характеристика функции одного действительного переменного, связанная с её дифференциальными свойствами. Для функции из отрезка на вещественной прямой в
 является обобщением понятия длины кривой, задаваемой в
является обобщением понятия длины кривой, задаваемой в  этой функцией.
этой функцией.Содержание
Определение
Пусть
![f:[a,\;b]\to\R^n](/pictures/wiki/files/51/330a298098e0d1e274b4d61a0b1cfc05.png) . Тогда вариацией (также полной вариацией или полным изменением) функции f на отрезке
. Тогда вариацией (также полной вариацией или полным изменением) функции f на отрезке ![[a,\;b]](/pictures/wiki/files/49/186c5c676bac5b18c4105688c2eb69d2.png) называется следующая величина:
называется следующая величина:то есть точная верхняя грань по всем разбиениям отрезка
![[a,\;b]](/pictures/wiki/files/49/186c5c676bac5b18c4105688c2eb69d2.png) длин ломаных в
длин ломаных в  , концы которых соответствуют значениям f в точках разбиения.
, концы которых соответствуют значениям f в точках разбиения.Связанные определения
- Функции, вариация которых ограничена на отрезке, называются функциями ограниченной вариации, а класс таких функций обозначается
![V[a,\;b]](/pictures/wiki/files/54/6713a1130c05ae7f7ae6eb602a6c5063.png) или просто V.
или просто V.
- В таком случае определена функция
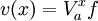 , называющаяся функцией полной вариации для f.
, называющаяся функцией полной вариации для f.
- В таком случае определена функция
- Положительная вариация вещественнозначной функции f на отрезке
![[a,\;b]](/pictures/wiki/files/49/186c5c676bac5b18c4105688c2eb69d2.png) называется следующая величина:
называется следующая величина:
- Аналогично определяется отрицательная вариация функции:
- Таким образом полная вариация функции может быть представлена в виде суммы
Свойства функций ограниченной вариации
- Сумма и произведение функций ограниченной вариации тоже будет иметь ограниченную вариацию. Частное двух функций из V будет иметь ограниченную вариацию (другими словами, принадлежать классу V), если модуль знаменателя будет больше, чем положительная постоянная на отрезке
![[a,\;b]](/pictures/wiki/files/49/186c5c676bac5b18c4105688c2eb69d2.png) .
. - Если
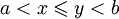 , а
, а ![f\in V[a,\;b]](/pictures/wiki/files/102/f1c4ad253a858d44958505e0deac4654.png) , то
, то 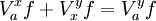 .
. - Если функция f непрерывна в точке a справа и принадлежит
![V[a,\;b]](/pictures/wiki/files/54/6713a1130c05ae7f7ae6eb602a6c5063.png) , то
, то 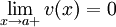 .
. - Функция f(x), заданная на отрезке
![[a,\;b]](/pictures/wiki/files/49/186c5c676bac5b18c4105688c2eb69d2.png) , является функцией ограниченной вариации тогда и только тогда, когда она может быть представлена в виде суммы возрастающей и убывающей на
, является функцией ограниченной вариации тогда и только тогда, когда она может быть представлена в виде суммы возрастающей и убывающей на ![[a,\;b]](/pictures/wiki/files/49/186c5c676bac5b18c4105688c2eb69d2.png) функции (разложение Жордана).
функции (разложение Жордана). - Всякая функция ограниченной вариации ограничена и может иметь не более чем счётное множество точек разрыва, причём все первого рода.
- Функция ограниченной вариации может быть представлена в виде суммы абсолютно непрерывной функции, сингулярной функции и функции скачков (разложение Лебега).
Все эти свойства были установлены Жорданом[1][2].
Вычисление вариации
Вариация непрерывно дифференцируемой функции
Если функция
![f:[a,\;b]\to\R^n](/pictures/wiki/files/51/330a298098e0d1e274b4d61a0b1cfc05.png) принадлежит классу C1, то есть имеет непрерывную производную первого порядка на отрезке
принадлежит классу C1, то есть имеет непрерывную производную первого порядка на отрезке ![[a,\;b]](/pictures/wiki/files/49/186c5c676bac5b18c4105688c2eb69d2.png) , то f — функция ограниченной вариации на этом отрезке, а вариация вычисляется по формуле:
, то f — функция ограниченной вариации на этом отрезке, а вариация вычисляется по формуле:то есть равна интегралу нормы производной.
История
Функции ограниченной вариации изучались К. Жорданом[1].
Первоначально класс функций с ограниченной вариацией был введён К. Жорданом в связи с обобщением признака Дирихле сходимости рядов Фурье кусочно монотонных функций. Жордан доказал, что ряды Фурье 2π-периодичических функций класса
![V[0,\;2\pi]](/pictures/wiki/files/48/0e543c8a86ee6df6356981f6c9e250c7.png) сходятся в каждой точке действительной оси. Однако в дальнейшем функции ограниченной вариации нашли широкое применение в различных областях математики, особенно в теории интеграла Стилтьеса.
сходятся в каждой точке действительной оси. Однако в дальнейшем функции ограниченной вариации нашли широкое применение в различных областях математики, особенно в теории интеграла Стилтьеса.Вариации и обобщения
Длина кривой определяется как естественное обобщение вариации на случай отображений в метрическое пространство.
В случае нескольких переменных существует несколько различных определений вариации функции:
- вариация Фреше,
- плоская вариация Тонелли.
Φ-вариация функции
Рассматривается также класс
![V_\Phi[a,\;b]](/pictures/wiki/files/54/6f7013a8f4796c22f9f416fe6f3059f0.png) , который определяется следующим образом:
, который определяется следующим образом:где Φ(x) (
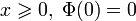 ) — положительная при x > 0 монотонно возрастающая непрерывная функция;
) — положительная при x > 0 монотонно возрастающая непрерывная функция;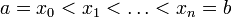 — произвольное разбиение отрезка
— произвольное разбиение отрезка ![[a,\;b]](/pictures/wiki/files/49/186c5c676bac5b18c4105688c2eb69d2.png) .
.Величина
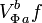 называется Φ-вариацией функции f(x) на отрезке
называется Φ-вариацией функции f(x) на отрезке ![[a,\;b]](/pictures/wiki/files/49/186c5c676bac5b18c4105688c2eb69d2.png) .
.Если
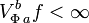 , то функция f(x) обладает ограниченной Φ-вариацией на отрезке
, то функция f(x) обладает ограниченной Φ-вариацией на отрезке ![[a,\;b]](/pictures/wiki/files/49/186c5c676bac5b18c4105688c2eb69d2.png) . Класс всех таких функций обозначается через
. Класс всех таких функций обозначается через ![V_\Phi[a,\;b]](/pictures/wiki/files/54/6f7013a8f4796c22f9f416fe6f3059f0.png) или просто как VΦ[3]. Определение класса
или просто как VΦ[3]. Определение класса ![V_\Phi[a,\;b]](/pictures/wiki/files/54/6f7013a8f4796c22f9f416fe6f3059f0.png) предложено Л. Янгом[4] (L. С. Yоung).
предложено Л. Янгом[4] (L. С. Yоung).Частным случаем классов Янга являются классы Жордана, при этом Φ(x) = x. Если Φ(x) = xp при
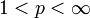 , то получаются классы Vp Н. Винера[5] (N. Wiener).
, то получаются классы Vp Н. Винера[5] (N. Wiener).Свойства
Если рассмотреть две функции Φ1(x) и Φ2(x) такие, что
то для их Φ-вариаций справедливо отношение:
В частности,
при
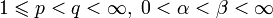 .
.См. также
- Вариация функционала
- Вариационное исчисление
- Вариационный ряд
- Интеграл Римана — Стилтьеса
- Вариация Арцела
- Вариация Витали
- Вариация Пъерпонта
- Плоская вариация Тонелли
- Вариация Фреше
- Вариация Харди
Литература
- Лебег, А. Интегрирование и отыскание примитивных функций / Пер. с франц. — М.—Л.: ОНТИ, 1934. — 324 с.
- Hатансон, И. П. Теория функций вещественной переменной. — М.: Наука, 1974. — 484 с.
- Бари, Н. К. Тригонометрические ряды. — М.: Государственное издательство физико-математической литературы, 1961. — 936 с.
Примечания
- ↑ 1 2 Jordan C. Comptes Rendus de l’Académie des Sciences. — 1881. — t. 92. — № 5. — p. 228—230.
- ↑ Hатансон, И. П. Теория функций вещественной переменной. — М.: Наука, 1974. — С. 234—238. — 484 с.
- ↑ Бари, Н. К. Тригонометрические ряды. — М.: Государственное издательство физико-математической литературы, 1961. — С. 287. — 936 с.
- ↑ Yоung L. С. Comptes Rendus de l’Académie des Sciences. — 1937. — t. 204. — № 7. — p. 470—472.
- ↑ Wiener N. Massachusetts Journal of Mathematics and Physics. — 1924. — v. 3. — p. 72—94.
Wikimedia Foundation. 2010.

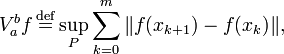
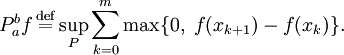
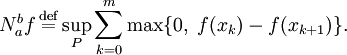
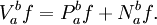
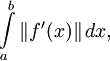
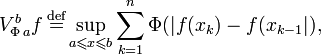
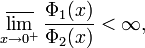
![V_{\Phi_2}[a,\;b]\subset V_{\Phi_1}[a,\;b].](/pictures/wiki/files/102/fa3ff00eb140d37d3385ee3eabc049e4.png)