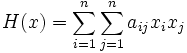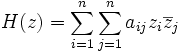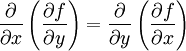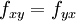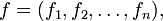- Определитель Гессе
-
Гессиан функции — симметрическая квадратичная форма описывающая поведение функции во втором порядке.
Для функции f дважды дифференцируемой в точке
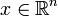
или
где
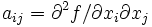 (или
(или 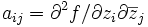 ) и f(p) задана на n-мерном вещественном пространстве
) и f(p) задана на n-мерном вещественном пространстве 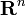 (или комплексном пространстве
(или комплексном пространстве 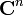 ) с координатами
) с координатами 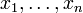 (или
(или 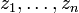 ). В обоих случаях гессиан — квадратичная форма, заданная на касательном пространстве, не меняющаяся при линейных преобразованиях переменных.
). В обоих случаях гессиан — квадратичная форма, заданная на касательном пространстве, не меняющаяся при линейных преобразованиях переменных.Содержание
Матрица Гессе
Матрица этой квадратичной формы образована вторыми частными производными функции. Если все производные существуют, то
Определитель этой матрицы называется определитель Гессе или также Гессианом.
Матрицы Гессе используются в задачах оптимизации в методе Ньютона. Полное вычисление матрицы Гессе может быть затруднительно, поэтому были разработаны квазиньютоновские алгоритмы, основанные на приближенных выражениях для матрицы Гессе. Наиболее известный такой алгоритм — алгоритм Бройдена — Флетчера — Гольдфарба — Шанно (англ.).
Симметрия Гессиана
Смешанные производные функции f — это элементы матрицы Гессе, стоящие не на главной диагонали. Если они непрерывны, то порядок дифференцирования не важен (теорема Клеро), например
Это можно также записать как
Формально, если вторые частные производные f — непрерывные в области D функции, то матрица Гессе симметрична на D.
Критические точки функции
Если градиент f (её векторная производная) равен нулю в некоторой точке x, то эта точка называется критической. Достаточные условия существования экстремума в этой точке является знакоопределённость Гессиана f, а именно:
- если Гессиан положительно определён и не вырожден, то x — точка локального минимума функции f;
- если Гессиан отрицательно определён и не вырожден, то x — точка локального максимума функции f;
- если Гессиан принимает как положительные, так и отрицательные значения, то x — седловая точка функции f;
Вариации и обобщения
Если f-векторнозначная функция, то есть
то её вторые частные производные образуют не матрицу, а тензор ранга 3.
История
Понятие введено Гессе (1844) который использовал другое название. Термин «Гессиан» был введён Сильвестром.
См. также
Ссылки
- Кудрявцев Л.Д «Краткий курс математического анализа. Т.2. Дифференциальное и интегральное исчисления функций многих переменных. Гармонический анализ», ФИЗМАТЛИТ, 2002, — 424 с. — ISBN 5-9221-0185-4
Wikimedia Foundation. 2010.