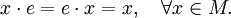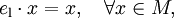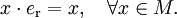- Нулевой элемент
-
Нейтра́льный элеме́нт бинарной операции — элемент, который оставляет любой другой элемент неизменным при применении этой бинарной операции к этим двум элементам.
Содержание
Определение
Пусть
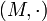 — множество M с определённой на нём бинарной операцией
— множество M с определённой на нём бинарной операцией  . Элемент
. Элемент 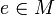 называется нейтральным относительно
называется нейтральным относительно  , если
, еслиИногда различают нейтральный слева элемент
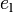 , для которого
, для которогои нейтральный справа элемент
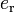 , для которого
, для которогоЗамечания
- В общем случае нейтральный слева и нейтральный справа элементы могут не совпадать или же не существовать.
- В приведённой выше мультипликативной нотации нейтральный элемент принято называть «единицей». Если для обозначения операции используется аддитивная нотация + , то нейтральный элемент называют «нулём» (не путать с числами 1 и 0, соответственно).
Примеры
Множество Бинарная операция Нейтральный элемент Вещественные числа + (сложение) число 0 Вещественные числа 
число 1 Вещественные числа ab (возведение в степень) число 1 (нейтральный справа) Матрицы размера 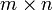
+ (матричное сложение) нулевая матрица Матрицы размера 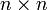
 (матричное произведение)
(матричное произведение)единичная матрица Функции вида 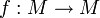
 (композиция функций)
(композиция функций)Тождественное отображение Функции вида 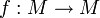
* (свёртка) δ (дельта-функция) Символьные строки конкатенация пустая строка Расширенная числовая прямая 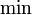 (минимум) или
(минимум) или 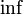 (инфимум)
(инфимум)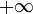
Расширенная числовая прямая 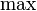 (максимум) или
(максимум) или 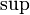 (супремум)
(супремум)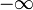
Подмножества множества M 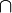 (пересечение множеств)
(пересечение множеств)M Множества 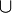 (объединение множеств)
(объединение множеств)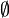 (пустое множество)
(пустое множество)Булева логика 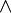 (логическое и)
(логическое и)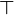 (истина)
(истина)Булева логика  (логическое или)
(логическое или)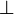 (ложь)
(ложь)См. также
Wikimedia Foundation. 2010.