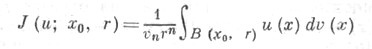Субгармоническая функция — Субгармонические и супергармонические функции представляют собой особые классы функций, содержащие как частные случаи, и класс гармонических функций. Содержание 1 Определение 2 Основные свойства … Википедия
Плюрисубгармоническая функция — Плюрисубгармноническая функция вещественнозначная функция , от комплексных переменных в области комплексного пространства , , удовлетворяющая следующим условиям … Википедия
Плюрисубгармноническая функция — Плюрисубгармноническая функция вещественнозначная функция u = u(z), от n комплексных переменных в области D комплексного пространства , , удовлетворяющая следующим условиям: u(z) полунепрерывна сверху всюду в … Википедия
Плюрисупергармоническая функция — Плюрисубгармноническая функция вещественнозначная функция u = u(z), от n комплексных переменных в области D комплексного пространства , , удовлетворяющая следующим условиям: u(z) полунепрерывна сверху всюду в … Википедия
ПЛЮРИСУБГАРМОНИЧЕСКАЯ ФУНКЦИЯ — действительная функция u=u(z), , п комплексных переменных z=(zl,. . ., zn).в области Dкомплексного пространства , удовлетворяющая следующим условиям: 1) и(z) полунепрерывна сверху всюду в D;2) u(z0+la). есть субгармоническая функция переменного в … Математическая энциклопедия
Гармоническая функция — Гармоническая функция вещественная функция , определенная и дважды непрерывно дифференцируемая на евклидовом пространстве (или его открытом подмножестве), удовлетворяющая уравнению Лапласа: где оператор Лапласа, то есть сумма вторых… … Википедия
ПОТЕНЦИАЛА ТЕОРИЯ АБСТРАКТНАЯ — теория потенциала на абстрактных топология, пространствах. П. т. а. возникла в сер. 20 в. из стремления охватить единым аксиоматич. методом широкое многообразие свойств различных потенциалов, применяемых при решении разнообразных задач теории… … Математическая энциклопедия
РИССА ТЕОРЕМА — 1) Р. т. о представлении субгармонической функции: если и(х) субгармонич. функция в области Dевклидова пространства , то существует единственная положительная борелевская мера m на Dтакая, что для любого относительно компактного множества… … Математическая энциклопедия
МАКСИМУМА МОДУЛЯ ПРИНЦИП — теорема, выражающая одно из основных свойств модуля аналитич. функции. Пусть f(z) регулярная аналитическая, или голоморфная, функция пкомплексных переменных в области Dкомплексного числового пространства отличная от константы, М. м. п. в… … Математическая энциклопедия
ФРАГМЕНА - ЛИНДЕЛЁФА ТЕОРЕМА — обобщение максимума модуля принципа аналитич. функций на случай функций, априори заданных как неограниченные; впервые в простейшей форме дано Э. Фрагмеyом и Э. Линделёфом [1]. Пусть f(z) регулярная аналитич. ция комплексного переменного zв… … Математическая энциклопедия
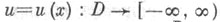точки х= (х 1, . . ., х п )евклидова пространства 
определенная в области 
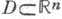и обладающая следующими свойствами: 1) и(х)полунепрерывна сверху в D;2) для любой точки 
существуют сколь угодно малые значения r>0 такие, что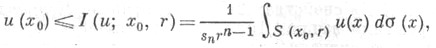 
- площадь единичной сферы в 
3) 
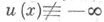(это условие иногда опускается). В данном определении С. ф. среднее значение I(и; х0, r )поплощади сферы можно заменить на среднее значение 
