РИССА ТЕОРЕМА

РИССА ТЕОРЕМА

- 1) Р. т. о представлении субгармонической функции: если и(х) - субгармонич. функция в области Dевклидова пространства , то существует единственная положительная борелевская мера m на Dтакая, что для любого относительно компактного множества справедливо п р е д с т а в л е н и е Р и с с а функции и(х)в виде суммы потенциала и гармонич. функции h(x):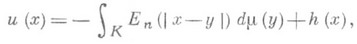

(4)

где


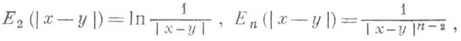
- расстояние между точками

(см. [1]). Мера m наз. а с с о ц и и р о в а н н о й мерой для функции и(х)или м е р о й Р и с с а.

Если есть замыкание области H, причем существует обобщенная функция Грина g(x, у; Н), то формулу (1) можно записать в виде

(2)

где h* (х) - наименьшая гармонич. мажоранта и(х)в области Н.

Формулы (1), (2) можно распространить при нек-рых дополнительных условиях на всю область D(см. Субгармоническая функция, а также [3], [5]).

2) Р. <т. о с р е д н е м з н а ч е н и и субгармонической функции: если и(х) -- субгармонич. функция в кольцевой области , то ее среднее значение но площади сферы S п (х 0,r) с центром х 0 и радиусом , равно


где sn(r) - площадь Sn(x0,r), и является выпуклой функцией относительно 1/rn-2 при и относительно Inr при n=2. Если же и(х) - субгармонич. функция во всем шаре , то J(r), кроме того,- неубывающая непрерывная функция относительно r при условии, что J(0) = u(x0 )(см. [1]).

3) Р. <т. об а н а л и т и ч е с к и х ф у н к ц и я х к л а с с о в Х а р д и Н d,d > 0: если f(z) - регулярная аналитич, функция в единичном круге класса Харди Н d,d > 0 (см. Граничные свойства аналитических функций), то для нее имеют место соотношения


где Е - любое множество положительной меры на окружности , f(eiq) - граничные значения f(z) на Г. Кроме того, тогда и только тогда, когда ее первообразная непрерывна в замкнутом круге и абсолютно непрерывна на Г (см. [2]). Теоремы 1) - 3) доказаны Ф. Риссом (см. [1], [2]).

Лит.:[1] R i e s z F., "Acta math.", 1926, v. 48, p. 329 - 43;1930, v. 54, p. 321-60; [2] e г о ж е, "Math. Z.", 1923, Bd 18. S. 87-95; [3] П р и в а л о в И. И., Субгармонические функции, М.-Л., 1937; [4] е г о ж е, Граничные свойства аналитических функций, 2 изд., М.-Л., 1950; [5] Х е й м а н У. К., К е н н е д и П. Б., Субгармонические функции, пер. с англ., т. 1, М., 1980. Е. Д. Соломенцев.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужно решить контрольную?

Полезное


Смотреть что такое "РИССА ТЕОРЕМА" в других словарях:

  • РИССА ТЕОРЕМА ВЫПУКЛОСТИ — логарифм In М(a, b) точной верхней грани модуля М(a, b) билинейной формы на множестве (если a=0 или b=0, то соответственно , тили ) является выпуклой функцией от параметров a и b в области , если форма действительна , и в области , если …   Математическая энциклопедия

  • Теорема представлений Рисса — Теорема Рисса (также теорема Рисса Фреше) в функциональном анализе утверждает, что каждый линейный ограниченный функционал в гильбертовом пространстве может быть представлен через скалярное произведение с помощью некоторого элемента. Названа в… …   Википедия

  • РИССА - ФИШЕРА ТЕОРЕМА — теорема, устанавливающая связь между пространствами l2 и L2.[а, b]:если система функций ортонормирована на отрезке [ а, b], а последовательность чисел такова, что (то есть ), то существует функция , для к рой При этом функция f(t)единственна как… …   Математическая энциклопедия

  • РИССА СИСТЕМА — понятие теории ортогональных систем Пусть фиксирована в пространстве L2=L2 ( а,b )полная система функций {yn}. Ее считают нормированной или, более общо, почти нормированной, т. е. допускают наличие чисел m> 0 и М >0, при к рых для всех .… …   Математическая энциклопедия

  • Теорема Лакса — Пусть: является гильбертовым пространством со скалярным произведением и ассоциированной нормой является билинейной формой, которая: непрерывна в коэрцитивна в …   Википедия

  • Теорема Рисса — …   Википедия

  • ГИЛЬБЕРТА НЕРАВЕНСТВО — теорема Гильберта о двойных рядах: где и ряды в правой части имеют конечные положительные суммы, причем константа точная, т. е. не может быть уменьшена. Д. Гильберт (D. Hilbert) доказал (*) без точной константы в своих лекциях но интегральным… …   Математическая энциклопедия

  • ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ — уравнение вида где F заданная действительная функция точки х=(xt, ..., х п )области Dевклидова пространства Е п, и действительных переменных (и(х) неизвестная функция) с неотрицательными целочисленными индексами i1 ,..., in, k=0, ..., т, по… …   Математическая энциклопедия

  • Гильбертово пространство — Сюда перенаправляется запрос «теорема Рисса Фишера». На эту тему нужна отдельная статья. Гильбертово пространство обобщение евклидова пространства, допускающее бесконечную размерность. Названо в честь Давида Гильберта. Со …   Википедия

  • ФУРЬЕ РЯД — функции f(х)по ортонормированной на промежутке ( а, b )системе функций ряд коэффициенты к рого определяются по формулам и наз. коэффициентами Фурье функции f. О функции f в общем случае предполагается, что она интегрируема с квадратом на ( а, b) …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»