СУБДИФФЕРЕНЦИАЛ

СУБДИФФЕРЕНЦИАЛ

выпуклой функции 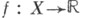в точке х 0, определенной на пространстве X, находящемся в двойственности с пространством Y- множество в Y, определяемое соотношением: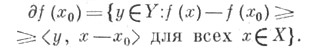

Напр., С. нормы 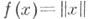в нормированном пространстве Xс сопряженным X* имеет вид

С. выпуклой функции f в точке х 0 является выпуклым множеством. Если f непрерывна в этой точке, то С. непуст и компактен в топологии
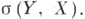
С. выпуклой функции играет роль, подобную роли производной в классич. анализе. Для него справедливы теоремы, аналогичные соответствующим теоремам для производной. Напр., если f1 и f2 - выпуклые функции и в нек-рой точке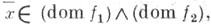 по крайней мере, одна из функций непрерывна, то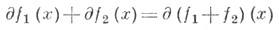


для всех х(теорема Моро - Рокафеллара).
С. опорной функции выпуклого множества Аиз X, компактного в топологии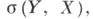 совпадает с самим множеством А. Это выражает двойственность между выпуклыми компактными множествами и выпуклыми замкнутыми однородными функциями (см. также Опорная функция, Падграфик, Выпуклый анализ).

Лит.:[1] Рокафеллар Р., Выпуклый анализ, пер. с англ., М., 1973.
В. М. Тихомиров.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужна курсовая?

Полезное


Смотреть что такое "СУБДИФФЕРЕНЦИАЛ" в других словарях:

  • Субдифференциал — функции f, заданной на банаховом пространстве E  это один из способов обобщить понятие производной на произвольные функции. Хотя при его использовании приходится пожертвовать однозначностью отображения (значения субдифференциала в общем… …   Википедия

  • ОПОРНАЯ ФУНКЦИЯ — опорный функционал, множества А, лежащего в векторном пространстве X, функция sA, задаваемая в находящемся с ним в двойственности векторном пространстве Y соотношением Напр., О. ф. единичного тара в нормированном пространстве, рассматриваемом в… …   Математическая энциклопедия

  • ПОЛУГРУППА НЕЛИНЕЙНЫХ ОПЕРАТОРОВ — однопараметрическое семейство операторов S(t),0 t< , определенных и действующих в замкнутом подмножестве Сбанахова пространства X, обладающее свойствами: 1) S(t+t)x= S(t)(S(t)x).при х С, t,t>0; 2) S(Q)x=x для любого х С; 3) при каждом х… …   Математическая энциклопедия

  • Опорная функция — или опорный функционал, множества , лежащего в векторном пространстве ,  функция , задаваемая на сопряжённом пространстве соотношением Например, опорная функция единичного шара в нормированном пространстве &# …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»