ПРОДОЛЖЕНИЯ ПО ПАРАМЕТРУ МЕТОД
- ПРОДОЛЖЕНИЯ ПО ПАРАМЕТРУ МЕТОД
включение данной задачи в однопараметрическое (0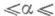 1) семейство задач, связывающее данную задачу (а=1) с известной разрешимой задачей (a=0), и изучение зависимости решений от параметра a. Метод широко используется в теории дифференциальных уравнений.
1) семейство задач, связывающее данную задачу (а=1) с известной разрешимой задачей (a=0), и изучение зависимости решений от параметра a. Метод широко используется в теории дифференциальных уравнений.
Пусть, напр., требуется доказать разрешимость в классе Гёльдера задачи Дирихле
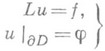 (1)
(1)
в ограниченной N-мерной области  для линейного эллиптич. оператора 2-го порядка
для линейного эллиптич. оператора 2-го порядка
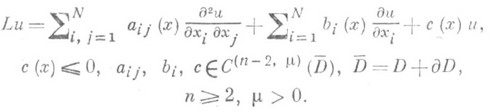
Вводится семейство эллиптич. операторов
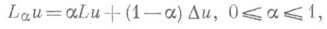
и рассматривается для него задача Дирихле
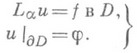 (2)
(2)
Пусть 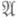 - множество тех
- множество тех 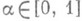 , для к-рых задача (2) однозначно разрешима в классе
, для к-рых задача (2) однозначно разрешима в классе 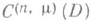 при любых f и
при любых f и 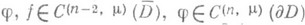 . Множество
. Множество 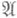 не пусто, поскольку при a=0 (т. е. для оператора Лапласа) задача (2) однозначно разрешима в классе
не пусто, поскольку при a=0 (т. е. для оператора Лапласа) задача (2) однозначно разрешима в классе 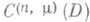 , как это следует из теории потенциала. Множество
, как это следует из теории потенциала. Множество 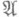 одновременно открыто и замкнуто на [0, 1] и; следовательно, совпадает с [0, 1]. Таким образом, a=1 принадлежит
одновременно открыто и замкнуто на [0, 1] и; следовательно, совпадает с [0, 1]. Таким образом, a=1 принадлежит 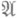 и задача (1) разрешима.
и задача (1) разрешима.
П. по п. м. (в варианте аналитич. родолжения по параметру) был предложен и развит в ряде работ С. Н. Бернштейна (см. [1], [2]). В дальнейшем этот метод нашел широкое применение в различных вопросах теории линейных и нелинейных дифференциальных уравнений, причем идея аналитич. родолжения по параметру была дополнена более общими функциональными и топологич. принципами (см. [3]).
Лит.:[1] Бернштейн С. Н., "Math. Ann.", 1904, Bd 59, S. 20-76; [2] его же, Собр. соч., т. 3, М., 1960; [3] Лерэ Ж., Шаудер Ю., "Успехи матеит. наук", 1946, в. 3/4, с. 71-95. И. А. Шишмарев.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "ПРОДОЛЖЕНИЯ ПО ПАРАМЕТРУ МЕТОД" в других словарях:
ПРОДОЛЖЕНИЯ ПО ПАРАМЕТРУ МЕТОД — метод приближенного решения нелинейных функциональных уравнений. П. по п. м. состоит в том, что решаемое уравнение Р(х)=0 обобщается к виду F(x, t)=0 путем введения параметра t, принимающего заданные значения на конечном интервале , так, что… … Математическая энциклопедия
ПАРАМЕТРА ВАРИАЦИИ МЕТОД — метод приближенного решения нелинейных (и линейных) функциональных и операторных уравнений в банаховых пространствах , а также для качественных исследований. П. в. м. состоит в том, что уравнение Р(х)=0, где оператор Р(х).непрерывно… … Математическая энциклопедия
УСТАНОВЛЕНИЯ МЕТОД — метод, заключающийся в том, что решение инек рых стационарных задач можно рассматривать как результат установления (при развивающегося во времени t>0 процесса u(t) решениях Коши задачи для нек рого нестационарного эволюционного уравнения с тем же … Математическая энциклопедия
ШАУДЕРА МЕТОД — метод решения краевых задач для линейных равномерно эллиптических уравнений 2 го порядка, в основе к рого лежат априорные оценки и метод продолжения по параметру. Ш. м. решения Дирихле задачи для линейного равномерно эллиптического уравнения… … Математическая энциклопедия
БЕРНШТЕЙНА ИНТЕРПОЛЯЦИОННЫЙ ПРОЦЕСС — последовательность алгебраич. многочленов, равномерно сходящаяся на отрезке [ 1,1] к функции , непрерывной на том же отрезке. Точнее, Б. и. п. последовательность алгебраич. многочленов где Чебышева многочлены; узлы интерполяции; если произвольное … Математическая энциклопедия
НЕПРЕРЫВНЫЕ АНАЛОГИ ИТЕРАЦИОННЫХ МЕТОДОВ — непрерывные модели, позволяющие исследовать вопросы существования решений нелинейных уравнений, проводить с помощью развитого аппарата непрерывного анализа предварительные исследования сходимости и оптимальности итерационных методов, получать… … Математическая энциклопедия
НЕЛИНЕЙНАЯ КРАЕВАЯ ЗАДАЧА — численные методы решения методы, заменяющие решение краевой задачи решением дискретной задачи (см. Линейная краевая задача;численные методы решения и Нелинейное уравнение;численные методы решения). Во многих случаях, особенно при рассмотрении… … Математическая энциклопедия
НЭША ТЕОРЕМЫ — в дифференциальной геометрии две группы теорем об изометрич. вложениях и погружениях римановых многообразий в евклидовы пространства, и первоначальные варианты к рых принадлежат Дж. Нэшу (J. Nash). 1) Н. т. о вложениях и погружениях. Погружение… … Математическая энциклопедия
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ — уравнение вида где F заданная действительная функция точки х=(xt, ..., х п )области Dевклидова пространства Е п, и действительных переменных (и(х) неизвестная функция) с неотрицательными целочисленными индексами i1 ,..., in, k=0, ..., т, по… … Математическая энциклопедия
ЛИНЕАРИЗАЦИИ МЕТОДЫ — методы, позволяющие свести решение нелинейных задач к последовательному решению родственных линейных задач. Пусть рассматривается нелинейное операторное уравнение где оператор Lотображает банахово пространство Нв себя, L(0)=0, и дифференцируем по … Математическая энциклопедия
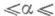 1) семейство задач, связывающее данную задачу (а=1) с известной разрешимой задачей (a=0), и изучение зависимости решений от параметра a. Метод широко используется в теории дифференциальных уравнений.
1) семейство задач, связывающее данную задачу (а=1) с известной разрешимой задачей (a=0), и изучение зависимости решений от параметра a. Метод широко используется в теории дифференциальных уравнений.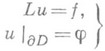 (1)
(1) для линейного эллиптич. оператора 2-го порядка
для линейного эллиптич. оператора 2-го порядка 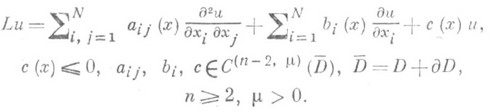
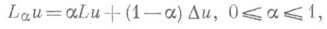
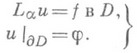 (2)
(2)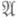 - множество тех
- множество тех 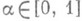 , для к-рых задача (2) однозначно разрешима в классе
, для к-рых задача (2) однозначно разрешима в классе 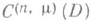 при любых f и
при любых f и 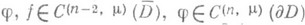 . Множество
. Множество 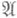 не пусто, поскольку при a=0 (т. е. для оператора Лапласа) задача (2) однозначно разрешима в классе
не пусто, поскольку при a=0 (т. е. для оператора Лапласа) задача (2) однозначно разрешима в классе 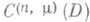 , как это следует из теории потенциала. Множество
, как это следует из теории потенциала. Множество 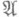 одновременно открыто и замкнуто на [0, 1] и; следовательно, совпадает с [0, 1]. Таким образом, a=1 принадлежит
одновременно открыто и замкнуто на [0, 1] и; следовательно, совпадает с [0, 1]. Таким образом, a=1 принадлежит 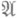 и задача (1) разрешима.
и задача (1) разрешима.