ШАУДЕРА МЕТОД

- метод решения краевых задач для линейных равномерно эллиптических уравнений 2-го порядка, в основе к-рого лежат априорные оценки и метод продолжения по параметру.
Ш. м. решения Дирихле задачи для линейного равномерно эллиптического уравнения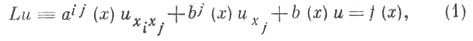

заданного в ограниченной области евклидова пространства точек x=(x₁, x₂, ..., х _п )и с коэффициентом описывается следующим образом.
1. Вводятся пространства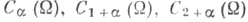 как множества функций u=и(x)с конечными нормами

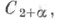2. Предполагается, что граница s области принадлежит классу т. е. каждый элемент -мерной поверхности может быть отображен на часть плоскости с помощью преобразования координат у=у (х)с положительным якобианом, причем функция

3. Доказывается, что если коэффициенты уравнения (1) принадлежат пространству и функция то справедлива априорная оценка вплоть до границы

где постоянная Сзависит только от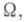 постоянной эллиптичности 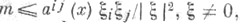и норм коэффициентов оператора L, а

4. Считается известным метод доказательства существования решения задачи Дирихле
для оператора Лапласа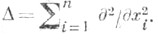

5. Не нарушая общности, полагается 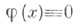и затем реализуется метод продолжения по параметру, сущность к-рого состоит в том, что:

Оператор Lвкладывается в однонараметрическое семейство операторов

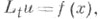
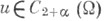Существенно опираясь на априорную оценку (2), устанавливается, что множество Ттех значений параметра для к-рых задача Дирихле имеет решение при любых является одновременно открытым и, стало быть, совпадает с единичным отрезком [0, 1].

6. Доказывается, что если D - ограниченная область, содержащаяся в вместе со своим замыканием, то для любой функции 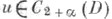и каждой компактной подобласти справедлива внутренняя априорная оценка:

7. Равномерно аппроксимируя заданные функции и f с помощью функций из класса и применяя оценку (3). показывается существование решения задачи Дирихле для любой непрерывной граничной функции и широкого класса областей с негладкими границами, напр, для областей, представимых как объединение последовательностей областей границы к-рых имеют такую же гладкость, что и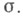
Оценки 2 и 3 получены впервые Ю. Шаудером (см. [1],[2])и носят его имя. Оценки Шаудера и его метод обобщены на уравнения и системы высшего порядка. Соответствующие им как внутренние, так и вплоть до границы, априорные оценки иногда наз. оценками шаудеровского типа. Дальнейшим развитием Ш. м. является метод априорных оценок.

Лит.:[l] Schauder J., лMath. 7.