- УСТАНОВЛЕНИЯ МЕТОД
- метод, заключающийся в том, что решение инек-рых стационарных задач
можно рассматривать как результат установления (при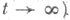
развивающегося во времени t>0 процесса u(t) - решениях Коши задачи для нек-рого нестационарного эволюционного уравнения с тем же оператором А, напр. вида 
здесь Ci - нек-рые операторы, гарантирующие существование процесса установления: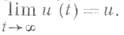
Эффект установления позволяет использовать приближенные методы решения задачи (2) для построения итерационных алгоритмов решения уравнения (1). Так, если для нестационарного уравнения (2) определен разностный, по tметод решения, обеспечивающий сходимость и устойчивость приближенного решения, напр. при m = 1 явный метод вида
где
то этот метод можно интерпретировать как итерационный алгоритм 
для решения уравнения (1), в к-ром С 1 п tn рассматриваются уже как характеристики метода.
Варьирование вида операторов Ci и рассмотрение различных аппроксимаций по tв уравнении (2) (явные, неявные схемы, схемы расщепления и т. п.) дают возможность получать достаточно разнообразные семейства итерационных методов решения уравнения (1). Для этих методов уравнение (2) будет замыканием вычислительного алгоритма.
Обобщением У. м. является продолжения по параметру метод.Лит.:[l] Бахвалов Н. С., Численные методы, 2 изд., М., 1975; [2] Годунов С. К., Рябенький В. С., Разностные схемы, 2 изд., М., 1977; [3] Марчук Г. П., Лебедев В. И., Численные методы в теории переноса нейтронов,
М., 1971. . В. И. Лебедев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
