- НЕПРЕРЫВНЫЕ АНАЛОГИ ИТЕРАЦИОННЫХ МЕТОДОВ
- непрерывные модели, позволяющие исследовать вопросы существования решений нелинейных уравнений, проводить с помощью развитого аппарата непрерывного анализа предварительные исследования сходимости и оптимальности итерационных методов, получать новые классы итерационных методов.
Можно установить соответствие между методами решения стационарных задач путем установления (см. Установления метод )и нек-рыми итерационными методами (см. [1], [2]). Напр., для решения линейного уравнения
 с положительно определенным самосопряженным оператором Аизвестны сходящиеся при достаточно малых
с положительно определенным самосопряженным оператором Аизвестны сходящиеся при достаточно малых  двучленные итерационные методы вида
двучленные итерационные методы вида
Если ввести непрерывное время t, а величины
 рассматривать как значение нек-рой функции
рассматривать как значение нек-рой функции  при
при  , где
, где 
если положить
 где непрерывная функция
где непрерывная функция  при
при  , то при переходе к пределу в (2) при
, то при переходе к пределу в (2) при  получают Н. а. и. м. (2):
получают Н. а. и. м. (2):
И если

при
 стремится к
стремится к  - решению уравнения (1).
- решению уравнения (1).Двучленным градиентным итерационным методам минимизации функции F(u):

аналогичным образом можно сопоставить Н. а. и. м. вида

Здесь функция
 влияет лишь на параметризацию линии наискорейшего спуска. Для решения уравнения (1) можно взять
влияет лишь на параметризацию линии наискорейшего спуска. Для решения уравнения (1) можно взять  тогда формулы (4) примут вид (2), а уравнение (5) - вид (3). Трехчленные итерационные методы:
тогда формулы (4) примут вид (2), а уравнение (5) - вид (3). Трехчленные итерационные методы:
с помощью преобразований можно записать в виде

где величины
 определяются (неоднозначно) по параметрам
определяются (неоднозначно) по параметрам  метода (6). Переход в (7) к пределу при
метода (6). Переход в (7) к пределу при  приводит к Н. а. и. м. вида
приводит к Н. а. и. м. вида
Метод установления с использованием уравнения типа (8) носит название метода тяжелого шарика (см. [2]). Существуют итерационные методы, для к-рых Н. а. и. м. содержат дифференциальные операторы более высоких порядков (см. [3]).
Источником получения дифференциальных уравнений, играющих роль Н. а. и. м., может быть метод продолжения по параметру (см. [4], [5]). В этом методе для нахождения решения уравнения

строят уравнение

зависящее от параметра
 и такое, что при
и такое, что при  решение
решение  известно:
известно: , а при
, а при 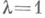 решения уравнений (9), (10) совпадают. Напр., можно взять
решения уравнений (9), (10) совпадают. Напр., можно взять
Дифференцируя уравнение (10) по параметру и считая
 , , получают дифференциальное уравнение для
, , получают дифференциальное уравнение для  ; оно для случая (11) примет вид
; оно для случая (11) примет вид
Разбивая отрезок [0, 1] на пчастей точками

 и применяя к уравнению (12) одну из формул численного интегрирования по точкам
и применяя к уравнению (12) одну из формул численного интегрирования по точкам  (метод Эйлера, Рунге - Кутта и т. п.), получают рекуррентные соотношения между величинами
(метод Эйлера, Рунге - Кутта и т. п.), получают рекуррентные соотношения между величинами  , к-рые используют для построения формул итерационного метода. Так, после применения метода Эйлера уравнение (12) заменится соотношениями
, к-рые используют для построения формул итерационного метода. Так, после применения метода Эйлера уравнение (12) заменится соотношениями
где
 к-рые определяют следующий двуступенчатый итерационный метод, содержащий внутренний п внешний циклы итераций:
к-рые определяют следующий двуступенчатый итерационный метод, содержащий внутренний п внешний циклы итераций:
При
 этот метод превращается в классич.
этот метод превращается в классич.метод Ньютона. Н. а. и. м. Ньютона может быть получен и другим путем: в формуле (11) заменяется переменная
 Тогда дифференциальное уравнение (12) принимает вид
Тогда дифференциальное уравнение (12) принимает вид
Численное интегрирование уравнения (15) методом Эйлера по точкам tk приводит к итерационному методу

совпадающему при
 с классич. методом Ньютона.
с классич. методом Ньютона.Н. а. и. м. решения краевых задач для дифференциальных уравнений математич. физики являются, как правило, смешанными задачами для уравнений с частными производными специального вида (напр., с быстро осциллирующими коэффициентами или с малыми коэффициентами при старших производных).
См. также ст. Замыкание вычислительного алгоритма.
Лит.:[1] Гавурин М. К., "Изв. ВУЗов. Математика", 1958, № 5(6), с. 18-31; [2] Бахвалов Н. С, Численные методы, 2 изд., т. 1, М., 1975; [3] Марчук Г. И., Лебедев В. И., Численные методы в теории переноса нейтронов, М., 1971; [4] Ортега Д., Рейнболдт В., Итерационные методы решения нелинейных систем уравнений со многими неизвестными, пер. с англ., М., 1975; [5] Давиденко Д. Ф., "Ж. вычисл. матем. и иатем. физ.", 1975, т. 15, .№ 1, с. 30-47.
В. И. Лебедев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
