ПОНТРЯГИНА ПРОСТРАНСТВО

гильбертово пространство с индефинитной метрикой 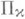, имеющей конечный ранг индефинитности 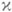. Основные факты геометрии П. п. установлены Л. С. Понтрягиным [1]. Помимо фактов, общих для пространств с индефинитной метрикой, имеют место следующие.

Если 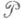- любой неотрицательный линеал в 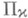, то ; если - положительный линеал и 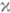, то его J-ортогональное дополнение Nявляется отрицательным линеалом и . При этом N представляет собой полное пространство по отношению к норме . Если линеал невырожден, то невырождено его J-ортогональное дополнение Ми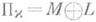

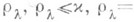
Спектр (в частности, дискретный спектр) J-унитарного (J-самосопряженного) оператора симметричен относительно единой окружности (действительной оси), все элементарные делители, отвечающие собственным числам l, |l|>1, имеют конечный порядок . Сумма размерностей корневых подпространств J-унитарного (J-самосопряженного) оператора, отвечающих собственным числам l, |l|>1 (Im l>0), не превосходит числа .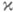

Основой теории J-самосопряженных операторов, действующих в П. и. , является следующая теорема [1]: у каждого J-самосопряженного оператора 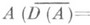) существует 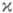-мерное (максимальное) неотрицательное инвариантное подпространство , в к-ром все собственные значения оператора Аимеют неотрицательную мнимую часть, и 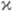-мерное неотрицательное инвариантное подпространство , в к-ром все собственные значения имеют неположительную мнимую часть. Аналогичное утверждение с заменой верхней (нижней) полуплоскости на внешность (внутренность) единичного круга справедливо и для J-унитарных операторов, а при нек-рых дополнительных условиях - даже для операторов в пространстве .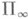

Если Uесть J-унитарный оператор, то его максимальные инвариантные неотрицательные подпространства 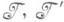могут быть выбраны таким образом, чтобы порядки элементарных делителей операторов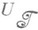 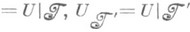были минимальны. Для того чтобы многочлен Р(l), не имеющий корней внутри единичного круга, обладал свойством: , необходимо и достаточно, чтобы он делился на минимальный аннулирующий многочлен оператора .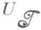

Если оператор U - циклический, то его неотрицательные инвариантные подпространства размерности определяются единственным образом. В этом случае указанное свойство многочлена Р, корни {l_i} к-рого лежат вне единичного круга |l_i|>1, эквивалентно делимости Р(l) на характеристич. многочлен оператора .

В П. п. 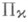у каждого вполне непрерывного J-самосопряженного оператора Атакого, что нуль принадлежит его непрерывному спектру, остаточный спектр отсутствует. Корневые векторы такого оператора образуют базис Рисса в по отношению к (дефинитной) норме (|J|x, х).

Многие факты об инвариантных подпространствах и спектре обобщаются на случай J-изометрических и J-нерастягивающих операторов. Так, если l₁, ... , l_n - произвольная совокупность собственных значений J-изометрического оператора, 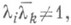i, k=l, ... , п, и порядок элементарного делителя в точке l_i, то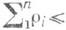 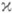. Всякий J-нерастягивающий ограниченно обратимый оператор Тобладает 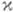-мерным инвариантным неотрицательным подпространством 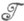таким, что все собственные значения сужения 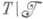лежат в единичном круге [2]. Аналогичный факт верен для максимальных J-диссипативных операторов. Вообще J-диссипативный оператор 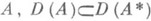, имеет не более 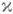собственных значений в верхней полуплоскости. Между J-изометрическими и J-симметрическими (и, более широко, J-нерастягивающими и J-диссипативными) операторами устанавливается связь с помощью Кали преобразования, к-рое в пространстве обладает всеми естественными свойствами [2]. Это позволяет развивать теорию расширений одновременно для J-изометрических и J-симметрических операторов. В частности, всякий J-изометрический (J-симметрический) оператор может быть расширен до максимального. Если его индексы дефекта не одинаковы, то у него нет J-унитарных (J-самосопряженных) расширений. Если же они одинаковы и конечны, то любое максимальное расширение является J-унитарным (J-самосопряженным).

Для вполне непрерывных J-диссипативных операторов в П. п. верен также ряд утверждений о полноте системы корневых векторов, аналогичных соответствующим фактам из теории диссипативных операторов в пространствах с дефинитной метрикой.

Лит.: [1] Понтрягин Л. С., "Изв. АН СССР. Сер. матем.", 1944, т. 8, с. 243-80; [2] Иохвидов И. С., Крейн М. Г., "Тр. Моск. матем. об-ва", 1956, т. 5, с. 367-432; [3] их же, там же, 1959, т. 8, с. 413-96; [4] Азизов Т. Я., Иохвидов И. С., "Успехи матем. наук", 1971, т. 26, в. 4, с. 43-92; [5] Крейн М. Г., в кн.: Вторая летняя математическая школа, [т.]1, К., 1965, с. 15-92; [6] Наймарк М. А., Исмагилов Р. С., в кн.: Итоги науки. Математический анализ, 1968, в. 17, М., 1969, с. 73-105; [7] Надь К., Пространства состояний с индефинитной метрикой в квантовой теории поля, пер. с англ., М., 1969.

Н. К. Никольский, Б. С. Подлов.