ГИЛЬБЕРТОВО ПРОСТРАНСТВО С ИНДЕФИНИТНОЙ МЕТРИКОЙ

- гильбертово пространство Е над полем комплексных чисел, снабженное непрерывной билинейной (точнее полуторалинейной) формой G, к-рая, вообще говоря, не является положительно определенной. Форму Gчасто наз. G-метрикой. Наиболее важным частным случаем Г. п. с и. м. является так наз. J-пространство: Г. п. с и. м., в к-ром форма Gопределяется нек-рой эрмитовой инволюцией J в Епо формуле . В этом случае форма G обозначается также буквой J и наз. J-метрикой. Инволюция допускает представление в виде - ортогональные проекторы в число наз. рангом индефинитности J-метрики или J-пространства. Если , то Г. п. с и. м. наз. Понтрягина пространством. см. также Пространство с индефинитной метрикой.

Два Г. п. с и. м. и наз. метрически эквивалентными, если существует линейный гомеоморфизм Uгильбертова пространства Ена пространство , переводящий форму G в форму G-метрика, порождаемая обратимым эрмитовым оператором G по формуле 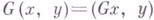, наз. регулярной; после введения нового скалярного произведения, метрически эквивалентного старому, регулярная G-метрика становится J-метрикой. Каждое Г. н. с и. м. с эрмитовой формой G может быть G-изометри-чески (т. е. с сохранением формы G) погружено в нек-рое J-пространство [2], [3].

Главные направления в теории Г. п. с и. м.- те же, что и в общих пространствах с индефинитной метрикой, но со значительным уклоном в спектральную теорию. Геометрия Г. п. с и. м. существенно богаче, чем у общих пространств с индефинитной метрикой. Так, в случае J-пространств имеется эффективное описание максимальных подпространств Lсреди всех неотрицательных (неположительных, нейтральных): это те L, для к-рых (соответственно выполнено хотя бы одно из этих равенств). Отсюда - аналог закона инерции квадратичных форм: если - канонич. разложение J-пространства в сумму семидефинитных подпространств, то Подпространство Lявляется максимальным неотрицательным тогда и только тогда, когда Lимеет угловой оператор K относительно Е ₊, т. е.

В J-пространствах развита теория базисов, к-рая помогает изучать геометрию Г. п. с и. м., а также операторы в них J-ортонормированный базис J-пространства есть базис в гильбертовом пространстве Е, удовлетворяющий условиям (, )= ; Для того чтобы J-ортонормированная последовательность была базисом Рисса пространства Е, необходимо и достаточно, чтобы где -замкнутая линейная оболочка векторов . Если -J-ортонормиро-ванный базис в Е, то разложение есть канонич. разложение J-пространства Е. Большую группу геометрич. задач в Г. п. с и. м., возникающих в теории операторов в этих пространствах, составляют вопросы, связанные со структурой и свойствами так наз. дуальных пар подпространств Г. п. с и. м. , т. е. таких пар N, Р подпространств в Е, что Nи Рвзаимно J-ортогональны, причем N-неположительное, а Р - неотрицательное подпространства. Дуальная пара наз. максимальной, если - максимальные семидефинитные подпространства.

Теория операторов в Г. п. с и. м. Метрика G считается эрмитовой и невырожденной, а встречающиеся операторы - плотно заданными. Пусть для оператора Тс областью определения D_T определен G-сопряжеиный оператор Т ^с равенством

При этом и

Оператор Тназ. G-cамосопряженным, если

, и G-c имметричным, если

Корневые подпространства (линеалы) G-симметричного оператора ТG-ортогональны; в частности, если то - нейтральное подпространство (линеал).

Если G - регулярная метрика, то спектр G-самосопряженного оператора Т симметричен относительно действительной оси; если - не регулярная, то это, вообще говоря, не так. J-самосопряженность оператора Травносильна самосопряженности JT. Если , то Кэли преобразование есть J-унитарный оператор, т. е. такой, что . Спектр симметричен относительно окружности .

Начиная с работы Л. С. Понтрягина [1], основным вопросом теории является вопрос о существовании семидефинитных инвариантных подпространств. Пусть Т - ограниченный оператор в J-пространстве и при , (так наз. плюс-оператор); если - вполне непрерывный оператор, то существует максимальное неотрицательное T-инвариантное подпространство L. Этот результат приложим, в частности, к J-унитарным операторам Uв пространствах , где он служит основой так наз. метода дефинизации - построения операторного полинома , переводящего Ев семидефинит-ное подпространство. Этот прием позволяет получать, напр., аналоги обычного спектрального разложения для J-унитарных и J-самосопряженных операторов в пространствах

Теория операторов в Г. п. с и. м. существенно используется в теории канонич. систем обыкновенных дифференциальных уравнений; напр., критерий устойчивости для таких уравнений следующим образом записывается в терминах оператора монодромии U:для этого необходимо и достаточно, чтобы существовала максимальная U-инвариантная дуальная пара подпространств. Другой основной потребитель описанной теории - спектральная теория квадратичных операторных пучков, важная во многих задачах математич. физики.

О теории представлений в Г. п. с и. м. см. [4].

Лит.:[l] Понтрягин Л. С., "Изв. АН СССР. Сер. матем.", 1944, т. 8, с. 243-80; [2] Гинзбург Ю. П., Иохвидов И. С., "Успехи матем. наук", 1962, т. 17, в. 4, с. 3- 56; [3] Азизов Т. Я., Иохвидов И. С., там же, 1971, т. 26, в. 4, с. 43-92; [4] Наймарк М. А., Исмагилов Р. С., Итоги науки. Математический анализ. 1968, М., 1969, с. 73-105; [5] Функциональный анализ, 2 изд., М., 1972 (Справочная математическая библиотека).

Н. Я. Никольский, Б. С. Павлов.