ПОНТРЯГИНА ПРИНЦИП МАКСИМУМА

соотношения, выражающие необходимые условия сильного экстремума для неклассической вариационной задачи оптимального управления математической теории. Сформулирован в 1956 Л. С. Понтрягиным (см. [1]).

Принятая формулировка П. п. м. относится к следующей задаче оптимального" управления. Дана система обыкновенных дифференциальных уравнений

(1)

где - фазовый вектор, -управляющий параметр, f - вектор-функция, непрерывная по совокупности переменных и непрерывно дифференцируемая по х. В пространстве задано множество Uдопустимых значений управляющего параметра и;в фазовом пространстве даны точки х ⁰ и х ¹;фиксирован начальный момент времени t₀. Допустимым управлением является любая кусочно непрерывная функция , со значениями во множестве U. Говорят, что допустимое управление u=u(t). переводит фазовую точку из положения х ⁰ в положение 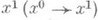, если соответствующее ему решение x(t).системы (1), удовлетворяющее условию x(t₀}=x⁰, определено при всех . Среди всех допустимых управлений, переводящих фазовую точку из положения х ⁰ в положение х ¹, требуется найти оптимальное управление - функцию u*(t), минимизирующую функционал

(2)

здесь f⁰(x, и) - заданная функция того же класса, что и компоненты f( х, и), x(t) - решение системы (1) с начальным условием x(t₀)=x⁰, отвечающее управлению u(t), t₁ - момент прохождения этого решения через точку х ¹. Под решением задачи понимают пару, состоящую из оптимального управления u*(t).и отвечающей ему оптимальной траектории x*(t).системы (1). Пусть

- скалярная функция (гамильтониан) переменных y, х, и, где

Функции H(y, x, и).ставится в соответствие каноническая (гамильтонова) система (относительно y, х)

(3) (первое из этих уравнений есть система (1)). Пусть

Принцип максимума Понтрягина: если - решение задачи оптимального управления (1), (2) , то существует такая ненулевая абсолютно непрерывная функция y(t), что тройка функций y(t), x*(t), и*(t).удовлетворяет на [t₀, t₁] системе (3) и для почти всех выполняется условие максимума

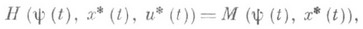(4) а в конечный момент t₁ - условия

(5)

Если функции y(t), x(t), u(t).удовлетворяют соотношениям (3), (4) (то есть х(t), u(t).образуют экстремаль Понтрягина), то имеют место условия

Из данного утверждения вытекает принцип максимума для задачи о быстродействии (f⁰=1, J=t₁-t₀). Это утверждение допускает естественное обобщение на неавтономные системы, задачи с подвижными концами траекторий и задачи сограничениями на фазовые координаты (условием 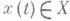, где X - замкнутое множество фазового пространства , удовлетворяющее нек-рым дополнительным ограничениям (см. [1])).

Допущение к рассмотрению замкнутых множеств U, X (эти области могут, в частности, задаваться системами нестрогих неравенств) обусловило неклассич. характер задачи. Основные необходимые условия классического вариационного исчисления с обыкновенными производными вытекают из П. п. м. (см. [1], а также Вейерштрасса условия).

Распространенное доказательство изложенной формулировки П. п. м., основанное на использовании т. н. игольчатых вариаций (т. е. на рассмотрении допустимых управлений, отклоняющихся от оптимального произвольным образом, но зато лишь на конечном числе малых интервалов времени), состоит в линеаризации задачи в окрестности оптимального решения, в построении нек-рого выпуклого конуса вариаций оптимальной траектории и последующем использовании теоремы об отделимости выпуклых конусов (см. [1]). Соответствующее условие далее записывается в аналитич. орме (4), (3), в терминах максимума гамильтониана H(y, х, и )от фазовых переменных х, управлений ии сопряженных переменных y, играющих роль, аналогичную Лагранжа множителям в классическом вариационном исчислении. Эффективное использование П. п. м. часто приводит к необходимости решать двухточечную краевую задачу для системы (3).

Наиболее полное решение задачи оптимального управления получено для линейных систем, где соотношения П. п. м. часто выступают не только как необходимое, но и как достаточное условие оптимальности.

П. п. м. получил многочисленные обобщения, напр., в направлении охвата более сложных неклассич. ограничений (в том числе смешанных ограничений на управления и фазовые координаты функциональных и разнообразных форм интегральных ограничений), в изучении достаточности соответствующих условий, в рассмотрении обобщенных решений, т. н. скользящих режимов, систем дифференциальных уравнений с негладкой правой частью, дифференциальных включений, задач оптимального управления для дискретных систем и систем с бесконечным числом степеней свободы, описываемых, в частности, уравнениями с частными производными, уравнениями с последействием (в том числе с запаздыванием), эволюционными уравнениями в банаховом пространстве и т. д. Последнее привело к рассмотрению новых классов вариаций соответствующих функционалов, введению т. н. интегрального принципа максимума, линеаризованного принципа максимума и т. д. Весьма общие классы вариационных задач с неклассич. ограничениями (в том числе в виде нестрогих неравенств) или. негладкими функционалами принято называть задачами понтрягинского типа. Открытие П. п. м. послужило важным стимулом в создании математич. теории оптимального управления. Оно стимулировало новые исследования в теории дифференциальных уравнений, функциональном анализе и теории экстремальных задач, вычислительной математике и других смежных областях.

Лит.:[1] Понтрягин Л. С., Болтянский В. Г., Гамкрелидзе Р. В., Мищенко Е. Ф., Математическая теория оптимальных процессов, 3 изд., М., 1976.

А. Б. Куржанский