- ОДНОЛИСТНАЯ ФУНКЦИЯ
- функция f, регулярная или мероморфная в области Врасширенной комплексной плоскости
 п такая, что для всяких zl ,
п такая, что для всяких zl ,  выполняется соотношение
выполняется соотношение 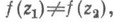 то есть f отображает В в
то есть f отображает В в  взаимно однозначно. При этом обратная функция
взаимно однозначно. При этом обратная функция  также однолистна.
также однолистна.Обобщением О. ф. являются многолистные функции, в частности р-листные функции.
При изучении О. ф. одним из основных является вопрос о возможности однолистного отображения заданной области В на заданную область В' (т. е. отображения с помощью О. ф.). Необходимым условием существования такого отображения является равенство порядков связности областей Ви В' (см., напр., [1] с. 28). Если Ви В' - односвязные области, границы к-рых содержат более одной точки, то это условие является и достаточным (см. Римана теорема )и задача сводится к отображению заданной области на круг. В связи с этим особую роль в теории О. ф. в односвязных областях играет класс S функций f, регулярных и однолистных в круге
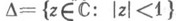 , нормированных условиями f(0) = 0, f' (0)=1 и имеющих разложение
, нормированных условиями f(0) = 0, f' (0)=1 и имеющих разложение
В случае многосвязных областей изучают отображение заданной многосвязной области на т. н. канонич. области (см. Конформное отображение). Пусть
 - класс функций F, мероморфных и однолистных в области В, содержащей точку
- класс функций F, мероморфных и однолистных в области В, содержащей точку 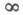 , и имеющих в окрестности точки
, и имеющих в окрестности точки  разложение
разложение
Если

то этот класс обозначают
 .
.Основные задачи теории О. ф. следующие: 1) изучение соответствия границ при конформном отображении (см. Соответствия границ принцип, Граничные элементы. Достижимая граничная точка);2) получение однолистности условий;3) решение различных экстремальных задач теории функций, в частности получение оценок различных функционалов и областей значений функционалов (см. ниже) и их систем в том или другом классе.
Пусть имеется нек-рый класс (множество) Крегулярных или мероморфных функций и пусть на Кзадан комплексный функционал
 (или система функционалов
(или система функционалов 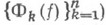 . Областью значений функционала
. Областью значений функционала 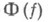 (или системы функционалов
(или системы функционалов  на классе Кназ. множество Dточек
на классе Кназ. множество Dточек  комплексного пространства
комплексного пространства  (соответственно множество точек
(соответственно множество точек  n-мерного комплексного пространства
n-мерного комплексного пространства 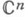 ) таких, что
) таких, что  . Рассматриваются также действительные функционалы. Всякое множество
. Рассматриваются также действительные функционалы. Всякое множество  , содержащее D, наз. мажорантной областью функционала (или системы функционалов). Знание области значений функционала позволяет свести решение ряда экстремальных задач к более простым задачам анализа. Напр., если известна область Dзначений функционала
, содержащее D, наз. мажорантной областью функционала (или системы функционалов). Знание области значений функционала позволяет свести решение ряда экстремальных задач к более простым задачам анализа. Напр., если известна область Dзначений функционала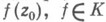 (z0 фиксировано), то задача оценки
(z0 фиксировано), то задача оценки  сверху и снизу сводится к нахождению самой далекой и самой близкой точек из Dпо отношению к точке w=0.
сверху и снизу сводится к нахождению самой далекой и самой близкой точек из Dпо отношению к точке w=0.Первые существенные результаты в теории О. ф. получены использованием площадей принципа. С помощью внешней теоремы площадей Л. Бибербах (L. Bieberbach, 1916) получил точные оценки
 и
и  сверху и снизу для
сверху и снизу для 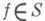 (см. Искажения теоремы), дал оценку
(см. Искажения теоремы), дал оценку  для
для  и высказал гипотезу, что
и высказал гипотезу, что  для
для  (см. Бибербаха гипотеза, Коэффици ентов проблема). Им же было найдено точное значение постоянной Кёбе. Были также получены оценки модуля функции, модуля ее производной и другие оценки в классах выпуклых функций, звездообразных функций, типично вещественных функций и др. В ряде классов были найдены выпуклости радиус и радиус звездообразности (см. Звездообразности граница).
(см. Бибербаха гипотеза, Коэффици ентов проблема). Им же было найдено точное значение постоянной Кёбе. Были также получены оценки модуля функции, модуля ее производной и другие оценки в классах выпуклых функций, звездообразных функций, типично вещественных функций и др. В ряде классов были найдены выпуклости радиус и радиус звездообразности (см. Звездообразности граница).Ниже приведены основные методы теории О. ф. и нек-рые результаты, полученные с их помощью.
1. Метод интегральных представлений дает возможность достаточно просто решать многие задачи теории функций, в частности экстремальные задачи в классах функций, имеющих представление с помощью интегралов Стилтьеса: выпуклых функций, почти выпуклых функций, звездообразных функций, типично вещественных функций, функций с положительной действительной частью (см. Каратеодори класс). Для классов функций, представимых посредством интеграла Стилтьеса, был разработан нек-рый вариационный метод (см. [1] с. 504-19), с помощью к-рого решен ряд экстремальных задач. Для таких классов разработан внутренних вариаций метод.
Найдены выпуклые оболочки нек-рых подклассов класса S(см. [3]). Здесь, в частности, доказано, что для всякой звездообразной функции f существует неубывающая на [0,2p] функция m такая, что
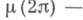
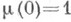 и
и
См. также Интегральное представление аналитической функции, Параметрическое представление, Параметрических представлений метод.
2. Метод контурного интегрирования. С помощью этого метода было, в частности, доказано, что для
 справедливо неравенство (см. [1]. с. 135-39)
справедливо неравенство (см. [1]. с. 135-39)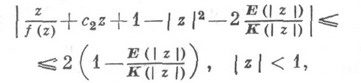
где
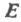 и
и  - полные эллиптические интегралы. Если zфиксировано
- полные эллиптические интегралы. Если zфиксировано  , то это неравенство определяет область значений функционала
, то это неравенство определяет область значений функционала 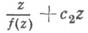 в классе S. Получены усиления теорем искажения и доказаны теоремы об искажении хорд в классах
в классе S. Получены усиления теорем искажения и доказаны теоремы об искажении хорд в классах 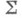 и
и  (см. Искажения теоремы и [1] с. 118-35).
(см. Искажения теоремы и [1] с. 118-35).См. также Контурного интегрирования метод, Площадей принцип.
3. Метод площадей. Пусть
 - класс систем функций
- класс систем функций 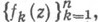 конформно и однолистно отображающих круг
конформно и однолистно отображающих круг  на области
на области  попарно не имеющие общих точек (неналегающие области), и нормированных условиями
попарно не имеющие общих точек (неналегающие области), и нормированных условиями  . С помощью теоремы площадей в классе
. С помощью теоремы площадей в классе  в частности, получены следующие результаты: 1) если
в частности, получены следующие результаты: 1) если 
то
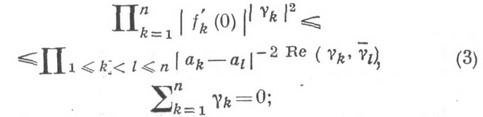
это неравенство обобщает на случай комплексных
 известное ранее неравенство для действительных
известное ранее неравенство для действительных  ; 2) если
; 2) если  то
то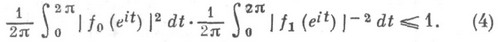
Для Бибербаха- Эйленберга функций
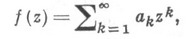
отсюда следует неравенство
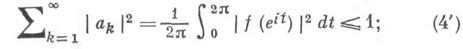
выяснены условия, при выполнении к-рых в (4) и (4') имеет место знак равенства.
С помощью теоремы площадей для неналегающих областей получена оценка приближения функции, регулярной на замкнутой многосвязной области, рациональной функцией, интерполирующей заданную функцию в узлах, равнорасположенных на границе области (см. [4] с. 143-54). Получена область значений шварциана

для
 и ряд других областей значений в классах функций, заданных в многосвязных областях (см. [4], [5]).
и ряд других областей значений в классах функций, заданных в многосвязных областях (см. [4], [5]).4. Метод Лёвнера. Сам К. Лёвнер (К. Lowner, 1923) получил точную оценку
 для функций
для функций  и точные оценки коэффициентов разложения функции, обратной к f , в окрестности точки
и точные оценки коэффициентов разложения функции, обратной к f , в окрестности точки 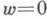 . В частности, этим методом получена точная форма теоремы вращения в классе S(см. Вращения теоремы). Доказана теорема: для
. В частности, этим методом получена точная форма теоремы вращения в классе S(см. Вращения теоремы). Доказана теорема: для  при заданных
при заданных  и
и 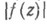 справедливо неравенство
справедливо неравенство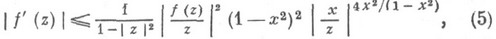
где
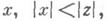 определяется условием
определяется условием
Неравенство (5) точное. Из (5) следуют точные неравенства в классе
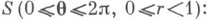

Был введен весьма широкий подкласс функций
 , представимых в виде
, представимых в виде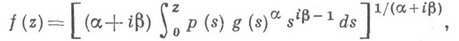
где g- звездообразная функция, р- регулярная в
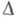 функция и такая, что
функция и такая, что  для нек-рого
для нек-рого (см.[6] с. 47).
(см.[6] с. 47).С помощью теорем искажения было установлено, что функция Кёбе

(
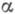 - действительное) реализует максимум линейной меры покрытия окружности
- действительное) реализует максимум линейной меры покрытия окружности 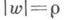 образом
образом  круга
круга  при отображении функциями класса S, когда
при отображении функциями класса S, когда 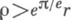 . Из этого свойства функций класса S следуют оценки площади
. Из этого свойства функций класса S следуют оценки площади 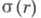 области
области 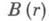 , оценки среднего модуля функции и другие оценки в классе S, асимптотически точные при
, оценки среднего модуля функции и другие оценки в классе S, асимптотически точные при  (см. [1] с. 561).
(см. [1] с. 561).Была предложена нек-рая удобная редукция экстремальных задач на классе Sи нек-рых его подклассах к определенным экстремальным задачам на более простом классе (см. Каратеодори класс), оказавшаяся применимой к решению ряда экстремальных задач, в частности к нахождению области значений системы функционалов
 (здесь
(здесь 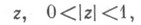 фиксировано) для
фиксировано) для  (см. [6] с. 115-58).
(см. [6] с. 115-58).Метод Лёвнера успешно применялся к исследованию свойств линий уровня и к решению экстремальных задач на подклассе
 ограниченных функций
ограниченных функций 
 (см. [6] с. 150-77).
(см. [6] с. 150-77).См. также Лёвнера уравнение, Лёвнера метод, Параметрических представлений метод.
5. Вариационные методы. Граничные и внутренние вариации при решении экстремальных задач приводят к дифференциальным уравнениям для границ экстремальных областей и, соответственно, для экстремальных функций. Левая часть этих уравнений, как правило, есть нек-рый квадратичный дифференциал. Различные качественные характеристики функций, реализующих экстремум, получаются при исследовании свойств соответствующих квадратичных дифференциалов. В частности, для большого числа экстремальных задач в классе S(и в других классах) оказывается, что экстремальная функция отображает круг D на всю плоскость с конечным числом аналитич. разрезов. Иногда дифференциальное уравнение для экстремальной функции удается проинтегрировать и тем самым получить величину экстремума в исследуемой задаче и все экстремальные функции. Чаще удается лишь получить одно или несколько конечных уравнений для величины экстремума. Нек-рые результаты, полученные вариационным методом, перечислены ниже.
Пусть
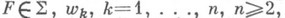 не принадлежат образу области
не принадлежат образу области  при отображении
при отображении  и пусть
и пусть 
Доказано, что
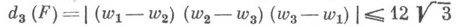
и знак равенства имеет место только для

где
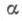 - действительное (см. [1] с. 140-46).
- действительное (см. [1] с. 140-46).Доказано (см. [1] с. 127-35), что область значений функционала
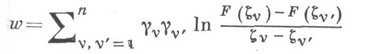
для
 , где
, где  - заданные числа, не равные одновременно нулю,
- заданные числа, не равные одновременно нулю, -заданные точки из области
-заданные точки из области  , является кругом
, является кругом
Исследована задача об экстремуме
 в классе
в классе 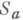 функций
функций 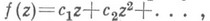 регулярных и однолистных в круге Д и не принимающих в нем заданных значений
регулярных и однолистных в круге Д и не принимающих в нем заданных значений  (см. [1] с. 151-56). Частный случай п=1 является задачей определения континуума наименьшей емкости (рассмотрение этой задачи и ее обобщений см. в [7]).
(см. [1] с. 151-56). Частный случай п=1 является задачей определения континуума наименьшей емкости (рассмотрение этой задачи и ее обобщений см. в [7]).С помощью вариационного метода исследовались различные задачи для неналегаюгцих областей. Так, рассматривалась задача о максимуме произведения
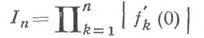
в классе
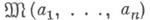 (см. [1] с. 156-65). Получена точная оценка произведения
(см. [1] с. 156-65). Получена точная оценка произведения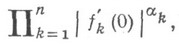
где
 - любые заданные положительные числа при ;
- любые заданные положительные числа при ; и 3 (см. [1] с. 550-51).
и 3 (см. [1] с. 550-51).Эта задача равносильна задаче нахождения области D системы функционалов
 в классе
в классе 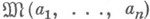 .
.См. также Вариационные принципы, Вариация однолистной функции, Внутренних вариаций метод, Граничных вариаций метод, Вариационно-параметрический метод.
6. Метод экстремальной метрики. При решении экстремальных задач методом экстремальной метрики основную роль, как правило, играет метрика, порожденная нек-рым квадратичным дифференциалом Q(z)dz2. Это тот же квадратичный дифференциал, к-рый возникает при решении задачи вариационным методом. Ниже для примера указаны два результата, полученные этим методом (см. [1] с. 532-611, [7] - [9]).
При помощи общей теоремы коэффициентов (о. т. к.) Дж. Дженкинс (J. Jenkins, 1960) получил решение задачи об области значений функционала
 при фиксированном z из круга
при фиксированном z из круга 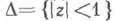 на классе
на классе 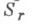 функций из Sс действительными коэффициентами
функций из Sс действительными коэффициентами  .... В классах
.... В классах  и М, где М- класс функций f,
и М, где М- класс функций f,  мероморфных и однолистных в круге
мероморфных и однолистных в круге  , он выяснил влияние обращения в нуль нек-рого числа из начальных коэффициентов на рост последующих.
, он выяснил влияние обращения в нуль нек-рого числа из начальных коэффициентов на рост последующих.Было дано добавление к о. т. к. в случае, когда дифференциал
 не имеет полюсов порядка, большего единицы; кроме того, с помощью экстремально-метрического подхода были установлены весьма общие теоремы покрытия линий при однолистном конформном отображении односвязных и двусвязных областей, в частности уточнен результат о покрытии отрезков для функций, мероморфных и однолистных в круге, и аналогичный результат для кругового кольца (см. [1] с. 559, 560, 564).
не имеет полюсов порядка, большего единицы; кроме того, с помощью экстремально-метрического подхода были установлены весьма общие теоремы покрытия линий при однолистном конформном отображении односвязных и двусвязных областей, в частности уточнен результат о покрытии отрезков для функций, мероморфных и однолистных в круге, и аналогичный результат для кругового кольца (см. [1] с. 559, 560, 564).См. также Грётша принцип, Грётша теоремы, Полос метод, Квадратичный дифференциал, Бибербаха- Эйленберга функции, Экстремальной метрики метод.
7. Метод симметризации. С помощью этого метода, часто в сочетании с другими, решен ряд сложных экстремальных задач, не поддающихся решению иными методами. Таковы, напр., следующие задачи (см. [1] с. 536-611, [7] - [10]). В классе Sфункций f была получена точная оценка сверху меры множества точек окружности
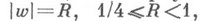 не принадлежащих образу круга
не принадлежащих образу круга  при отображении
при отображении  .
.В сочетании с методом экстремальных метрик найдена точная оценка сверху
 при фиксированном
при фиксированном 
 для
для 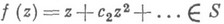 с заданным
с заданным  обобщены и распространены неравенства (6) на класс р-листных в среднем по окружности функций
обобщены и распространены неравенства (6) на класс р-листных в среднем по окружности функций
(см. Многолистная функция).
С использованием метода симметризации было доказано, что если Ф - выпуклая неубывающая на
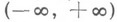 функция, то для
функция, то для  при
при 
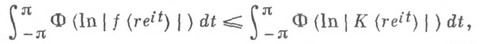
где
 (см. [11]). Если имеет место знак равенства при нек-ром
(см. [11]). Если имеет место знак равенства при нек-ром  и при нек-рой строго выпуклой функции Ф, то
и при нек-рой строго выпуклой функции Ф, то  где a. действительно.
где a. действительно.О приложениях метода симметризации к многосвязным областям см. в [12], [13]. См. также Симметризации метод.
Лит.:[1] Голузин Г. <М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; [2] Александров И. А., Лебедев Н. А., "Тр. Матем. ин-та АН СССР", 1968, т. 94, с. 79-89; [3] Вriсkman L., Мас Gregor Т. Н., Wilken D. R., "Trans. Amer. Math. Soc", 1971, v. 156, p. 91-107; [4] Лебедев Н. А., Принцип площадей в теории однолистных функций, М., 1975; [5] Милин И. М., Однолистные функции и ортонормированные системы, М., 1971; [6] Александров И. А., Параметрические продолжения в теории однолистных функций, М., 1976; [7] Кузьмина Г. В., "Тр. Матем. ин-та АН СССР", 1980, т. 139, с. 1-241; [8] Дженкинс Дж., Однолистные функции и конформные отображения, пер. с англ., М., 1962: [9] Роmmеrеnke Сh., Univalent Functions, Gott., 1975; [10] Хейман В. К., Многолистные функции, пер. с англ., М., 1960; [11] Baernstein A., "Acta math.", 1974, v. 133, p. 139-69; [12] Mитюк И. П., "Укр. матем. ж.", 1965, т. 17, № 4, с. 46-54; [13] его же, "Сиб. матем. ж.", 1965, т. 6, №6, с. 1282-91.
Н. А. Лебедев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
