ОГРАНИЧЕННЫЙ ОПЕРАТОР

ОГРАНИЧЕННЫЙ ОПЕРАТОР

- отображение А топологического векторного пространства Xв топологическое векторное пространство Y такое, что (М)- ограниченное подмножество в Yдля любого ограниченного подмножества Мпространства X. Всякий оператор 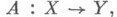непрерывный на X, является О. о. Если - линейный оператор, то для ограниченности Адостаточно, чтобы существовала окрестность нуля такая, что A(U)ограничено в Y. Пусть X,Y - векторные нормированные пространства и линейный оператор 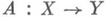ограничен. Тогда

Это число наз. нормой оператора Аиобозначается . При этом

и 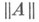есть наименьшая из констант Стаких, что

для любого 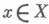. Обратно, выполнение этого неравенства означает, что Аограничен. Для линейных операторов, отображающих нормированное пространство Xв нормированное пространство У, понятия ограниченности и непрерывности эквивалентны. Для случая произвольных топологических векторных пространств Xи Y это не так, но если X - борнологическое, Y- локально выпуклое пространство, то из ограниченности линейного оператора следует его непрерывность. Если Н- гильбертово пространство и - ограниченный симметрич. оператор, то квадратичная форма <Ах, x> ограничена на единичном шаре 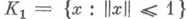. Числа

наз. верхней и нижней границами оператора А. Точк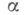и и принадлежат спектру A, и весь спектр лежит на отрезке . Примеры О. о.: оператор проектирования (проектор )на дополняемое подпространство банахова пространства и изометрический оператор, действующий в гильбертовом пространстве.

Если пространства Xи Yнаделены структурой частично упорядоченного множества, напр, являются векторными решетками, то помимо рассмотренной выше топологич. ограниченности вводится понятие порядковой ограниченности оператора. Именно, оператор 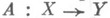паз. порядково ограниченным, если (М)есть порядково ограниченное множество пространства Yдля любого порядково ограниченного множества Мпространства X. Пример: изотонный оператор, т. е. такой оператор, что из 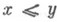следует

Лит.:[1] Люстерник Л. А., Соболев В. И., Элементы функционального анализа, 2 изд., М., 1965: [2] Рудин У., Функциональный анализ, пер. с англ., М., 1975; [3] Биркгоф Г., Теория структур, пер. с англ., М., 1952.

В. И. Соболев.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем сделать НИР

Полезное


Смотреть что такое "ОГРАНИЧЕННЫЙ ОПЕРАТОР" в других словарях:

  • Ограниченный оператор — Оператор называется ограниченным, если каждое ограниченное множество исходного топологического векторного пространства он переводит в ограниченное множество топологического векторного пространства .[1] Приведённое выше определение относится как к …   Википедия

  • Оператор Гильберта — Шмидта — это ограниченный оператор A на гильбертовом пространстве H с конечной нормой Гильберта Шмидта, т.е. для которого существует такой ортонормированный базис в H, что Если это верно в каком то ортономированном базисе, то это верно в любом… …   Википедия

  • Оператор Гильберта — Шмидта это ограниченный оператор на гильбертовом пространстве с конечной нормой Гильберта Шмидта, т. е. для которого существует такой ортонормированный базис в , что Если это верно в каком то ортономированном базисе, то это верно в любом… …   Википедия

  • Строго сингулярный оператор — Ограниченный линейный оператор между нормированными пространствами называется строго сингулярным если его сужение на любое бесконечномерное подпространство не является изоморфизмом. То есть, оператор в   строго сингулярен если для любого… …   Википедия

  • Ограниченный линейный оператор — Линейный оператор из нормированного пространства в нормированное пространство называется ограниченным если найдётся положительное вещественное число такое, что для всех в . Наименьшая константа …   Википедия

  • ЗАМКНУТЫЙ ОПЕРАТОР — оператор А: такой, что из и следует и Ах=у (здесь X, Y банаховы пространства над одним и тем же полем скаляров и область определения оператора А). Понятие 3. о. распространяется и на операторы, действующие в отделимых линейных топологич.… …   Математическая энциклопедия

  • Непрерывный линейный оператор — Линейный непрерывный оператор дейсвтующий из X в Y( ) это линейное отображение из X в Y обладающее свойством непрерывности. Термин линейный непрерывный оператор обычно употребляют в случае, когда . Если …   Википедия

  • Линейный непрерывный оператор — Линейный непрерывный оператор, действующий из в ( ) это линейное отображение из в , обладающее свойством непрерывности. Термин линейный непрерывный оператор обычно употребляют в случае, когда . Если …   Википедия

  • НЕЛИНЕЙНЫЙ ОПЕРАТОР — отображение А векторного (как правило) пространства Xв векторное пространство Yнад общим полем скаляров, не обладающее свойством линейности, т. е. такое, что, вообще говоря, Если есть множество действительных чисел или комплексных чисел , то Н. о …   Математическая энциклопедия

  • ПРОИЗВОДЯЩИЙ ОПЕРАТОР — полугруппы производная в нуле от полугруппы линейных ограниченных операторов , действующих в комплексном банаховом пространстве X. Если T(t).непрерывна по норме операторов, то она имеет вид T(t)= е tA0, где А 0 ограниченный оператор, (1) при… …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»