ЗВЕЗДООБРАЗНАЯ ФУНКЦИЯ

однолистная звездообразная функци я,- функция w=f(z), регулярная и однолистная в круге |z|<l, f(0)=0, и такая, что она отображает |z|<l на звездообразную область, относительно точки w=0. Для того, чтобы функция f(z), в 0<|z|<1,/(0) = 0, регулярная в круге |z|<l, была в нем 3. ф., необходимо и достаточно, чтобы она удовлетворяла условию:

Все 3. ф. в |z|<l, нормированные условиями f(0)=0, f' (0)=1, образуют класс S*, для к-рого имеет место параметрическое представление интегралом Стилтьеса

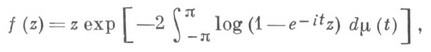
где m(t) - неубывающая функция на [-p, p],m(p) -m(-p)=1.

Для класса S* решена коэффициентов проблема, найдены точные оценки для |f(z)|, |f '(z)|, arg f(z),arg f' (z) (под аргументом функции понимается ветвь, обращающаяся в нуль при z=0), причем экстремальными функциями этих оценок являются функции f(z)=z/(l-e^iqz)², где 6 вещественно. Класс S* функций f(z) связан с классом функций j(z), j(0)=0, j'(0)=1, регулярных и однолистных в |z|<l, отображающих |z|<l на выпуклую область, по формуле: zj'(z)=f(z).

З. ф., удовлетворяющая условию

наз. З. <ф. порядка а в круге z<1.

Рассматривались также однолистные 3. ф. в кольце (см. [1] с. 586-87), р-листные 3. ф. и слабо 3. ф. в круге (см. [2], [4]), Е-локально звездные функции (см. [1] с. 584), функции, звездообразные в направлении действительной оси (см. [3]). Относительно 3. ф. многих комплексных переменных см. [5].

Лит.:[1] Голузин Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; [2] Нummel J. A., "J. d'Analyse math.", 1967, v. 18, p. 133-60; [3] Robertson M. S., "Amer. J. Math.", 1936, v. 58, № 3, p. 465-72; [4] Gооdman A. W., "Bull. Amer. Math. Soc", 1968, v. 74, № 6, p. 1035-50; [5] Баврин И. И., Классы голоморфных функций многих комплексных переменных и экстремальные вопросы для этих классов функций, М., 1976.

Е. Г. Голузина.