- МЕРА
в топологическом векторном пространстве - термин, употребляемый применительно к мере, заданной в топологическом векторном пространстве, когда хотят подчеркнуть те свойства этой меры, к-рые связаны с линейной и топологич. структурой этого пространства. Общей проблемой при построении М. в топологич. векторном пространстве является задача продолжения предмеры до М. Пусть Е- (действительное или комплексное) локально выпуклое пространство,
 - алгебра его цилиндрических множеств и на алгебре
- алгебра его цилиндрических множеств и на алгебре 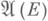 определена, пред-мера. Задача состоит в продолжении этой предмеры до счетно аддитивной М., определенной на s-алгебре
определена, пред-мера. Задача состоит в продолжении этой предмеры до счетно аддитивной М., определенной на s-алгебре 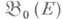 - наименьшей s-алгебре, содержащей алгебру
- наименьшей s-алгебре, содержащей алгебру 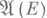 ;
; 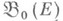 - самая узкая из всех s-алгебр (слабоборелевской, борелевской и т. д.), естественно связанных с топологией Е;для большого класса пространств Еэти s-алгебры совпадают. В частном, но наиболее важном случае, когда пространство
- самая узкая из всех s-алгебр (слабоборелевской, борелевской и т. д.), естественно связанных с топологией Е;для большого класса пространств Еэти s-алгебры совпадают. В частном, но наиболее важном случае, когда пространство 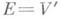 , т. е. является сопряженным к нек-рому локально выпуклому пространству V, рассматриваемому в слабой "-топологии (так что
, т. е. является сопряженным к нек-рому локально выпуклому пространству V, рассматриваемому в слабой "-топологии (так что 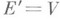 ), для продолжимости предмеры
), для продолжимости предмеры  в
в  до М. достаточно, чтобы ее характеристич. функционал (преобразование Фурье)
до М. достаточно, чтобы ее характеристич. функционал (преобразование Фурье)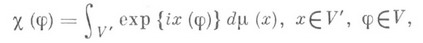
был непрерывен в т. н. топологии Сазонова в пространстве V(т. е. топологии, порожденной всеми непрерывными гильбертовыми полунормами в V), и в ряде случаев, напр, когда V- Фреше пространство, необходимо, чтобы характеристич. функционал был непрерывен в исходной топологии V. Так, когда V- ядерное пространство, топология Сазонова совпадает с исходной топологией, и любая предмера на Vс непрерывным характеристич. функционалом продолжается до М. В случае, когда предмера определена в гильбертовом пространство Н, сформулированное выше достаточное условие ее продолжимости до М. является и необходимым. Кроме этого общего критерия продолжимости предмеры до М. существуют частные результаты такого рода, приложимые к тому или иному классу М. (или классу пространств). Напр., гауссова предмера на V, где V- локально выпуклое пространство (т. е. предмера, сужение к-рой на любую s-алгебру
 является гауссовым распределением с корреляционным функционалом
является гауссовым распределением с корреляционным функционалом 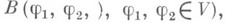 продолжается до М., если существует выпуклая окрестность нуля в V,
продолжается до М., если существует выпуклая окрестность нуля в V, -энтропия к-рой в метрике, порожденной скалярным произведением
-энтропия к-рой в метрике, порожденной скалярным произведением  меньше двух.
меньше двух.Для слабой сходимости последовательности (вероятностных) М. в сопряженном пространстве Vдостаточны поточечная сходимость характеристич. функционалов этих М. (она же и необходима) и равностепенная непрерывность их в нуле относительно топологии Сазонова в V, а необходима равностепенная непрерывность этих функционалов относительно исходной топологии V. В случае, когда V- гильбертово пространство, известны необходимые и достаточные условия слабой компактности семейства М. в V, также выражающиеся в терминах их характеристич. функционалов. Вопрос о квазиинвариантности М. в топологическом векторном пространстве (см. Квазиинвариантная мера )относительно нек-рой совокупности сдвигов (множества квазиинвариантности) этого пространства (известно, что для ряда бесконечномерных векторных пространств множество квазиинвариантности ненулевой М. не может совпадать со всем пространством), а также вопрос о критериях абсолютной непрерывности одной М. относительно другой исследованы лишь (1982) для гауссовых М. Изучение М. в топологических векторных пространствах связано главным образом с интегралами по траекториям, а также с теорией обобщенных случайных полей и в значительной степени стимулируется приложениями этих теорий к физике и механике.
Лит.:[1] Данфорд Н., Шварц Дж., Линейные операторы. Общая теория, пер. с англ., М., 1962; [2] Бурбаки Н., Интегрирование. Меры на локально компактных пространствах. Продолжение меры. Интегрирование мер. Меры на отделимых пространствах, пер. с франц., М., 1977; [3] Гихман И. И., Скороход А. В., Теория случайных процессов, т. 1, М., 1971: [4] Гельфанд И. М., Виленкин Н. Я., Некоторые применения гармонического анализа. Оснащенные гильбертовы пространства, М., 1961; [5] Судаков В. Н., "Тр. Матем. ин-та АН СССР", 1976, т. 141; [6] Смолянов О. Г., Фомин С. В., "Успехи матем. наук", 1976, т. 31, в. 4, с. 3 - 56. Р. А. Минлос.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
