КОШИ ИНТЕГРАЛ

- 1) К. и. - определенный интеграл от непрерывной функции одного действительного переменного. Пусть функция f(x).непрерывна на отрезке

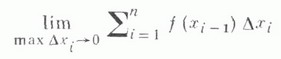
наз. определенным интегралом по К о ш и от функции f(x) на отрезке [ а, b]и обозначают

К. и. - частный случай Римана интеграла. Определение дано О. Конш в [1].

Лит.:[1] С а u с h у A. L., Resume des lecons donnees ft l'Ecole Royale Polytechnique sur le calcul infinitesimal, t. 1, P., 1823. Л. Д. Кудрявцев.

2) К. и. - интеграл с ядром Коши

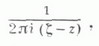
выражающий значения регулярной аналитич. функции f(z) внутри контура Lчерез ее значения на L. Точнее, пусть f(z) - регулярная аналитич. функция комплексного переменного z в области Dи L - замкнутая кусочно гладкая жорданова кривая, расположенная в Dвместе со своей внутренностью G, причем обход Lсовершается против часовой стрелки. Тогда справедлива основная в теории аналитич. функций одного комплексного переменного интегральная формула Коши:

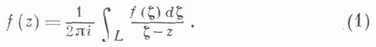
Стоящий справа в формуле (1) интеграл и наз. интегралом Коши. Впервые, по-видимому, К. и., применительно к частным ситуациям, появляется в работах О. Коши [1].

К. и. характеризуется, таким образом, двумя условиями: 1) К. и. берется по замкнутой гладкой или хотя бы кусочно гладкой кривой L;2) подинтегральная функция К. и. имеет вид

где 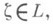а f(z) - регулярная аналитич. функция на Lи внутри Л. Если в К. и. т. е. если z расположена во внешности кривой L, то при сохранении условий 1) и 2):

В частности, если L - окружность радиуса р с центром z, т. е.

то из (1) следует

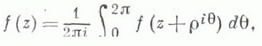
т. е. значение f(z) в любой точке равно среднему арифметическому ее значений на любой достаточно малой окружности с центром z. Формула (1) позволяет получить и все остальные элементарные свойства аналитич. функций.

Если, с другой стороны, f(z).является регулярной аналитич. функцией в бесконечной области - внешности замкнутой кривой Lи на L,

то справедлива интегральная формула Коши для бесконечной области:

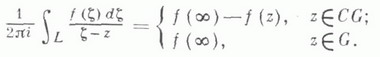
Пусть теперь Г - некоторая, не обязательно замкнутая, кусочно гладкая кривая, расположенная в конечной плоскости - непрерывная комплексная функция на Г и z - точка, не лежащая на Г. И н т е г р а л о м типа Коши (и. т. К.) наз. обобщение К. и. в виде

Функцию наз. иногда плотностью интеграла типа Кош и. Простейшие свойства и. т. К.:

1) F(z) - регулярная аналитич. функция переменного z в любой области, не содержащей точек Г;

2) производные F⁽ⁿ⁾(z) выражаются формулами

3) функция регулярна в бесконечности, причем 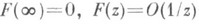при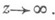

С точки зрения общей теории аналитич. функций и применений к механике и физике, основное значение имеет вопрос о существовании граничных значений и. т. К. при приближении к Г и об их аналитич. выражении. К. <и. (1) всюду внутри Lравен f(z), а во внешности он тождественно равен нулю. Поэтому, когда и. <т. К. (3) обращается в К. и., т. е. когда выполняются условия 1) и 2), функция F(z).при приближении к Lслева (т. е, изнутри) имеет граничные значения и при этих значениях на Lона непрерывна в каждой точке слева от L;при приближении к Lсправа (т. е. извне) F(z).имеет граничные значения нуль, и при этих значениях на Lона непрерывна в каждой точке 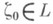справа от L. Т. обр., для К. и.

Для и. т. К. общего вида дело обстоит несколько сложнее. Пусть кривая Г задана уравнением s - длина ее дуги, отсчитываемая от какой-либо фиксированной точки, 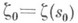- произвольно фиксированная точка на - та часть кривой Г, к-рая остается после удаления из Г меньшей дуги с концами Если существует конечный предел

то он наз. сингулярным, или особым, интегралом. Доказано, напр., что сингулярный интеграл (4) существует, если кривая Г гладкая в окрестности отличной от концов Г точки а плотность удовлетворяет условию Гёльдера

При этих условиях существуют и граничные значения, к-рые выражаются формулами Сохоцкого:

а функции F⁺(z).и F^-(z) - непрерывны в окрестности соответственно слева и справа от Г. В случае К. и. сингулярный интеграл равен

В эквивалентной форме формулы (5) записываются так:

Формулы Сохоцкого (5) - (7) имеют основное значение при решении граничных задач теории аналитических функций, сингулярных интегральных уравнений, связанных с и. т. К., а также при решении ряда задач гидродинамики, теории упругости и др.

Пусть Г - произвольная, для простоты замкнутая, спрямляемая кривая длины 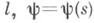- угол между направлением оси Ох и касательной к Г в точке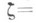 рассматриваемый как функция длины дуги s, Ф(s) - комплексная функция длины дуги s ограниченной вариации на [О, I]. Выражение

ваз. интегралом типа Коши и - Cтильеса (и. т. К.-С.). Иначе говоря, и. т. К.-С. есть и. т. К. по произвольной конечной комплексной борелевской мере, сосредоточенной на Г. Если функция Ф(s) абсолютно непрерывна, то и. т. К.-С. превращается в интеграл типа Кош и - Лебега (и. т. К.-Л.), часто называемый также просто интегралом типа Коши:

Пусть - точка Г , в к-рой существует определенная касательная, наклоненная к оси Ох под углом такие точки имеются на спрямляемой кривой почти всюду. Пусть точка z находится на нек-рой прямой, проходящей через и наклоненной к нормали под углом а ₀, на

расстоянии

Разность между и. т. К.- С. (8) и интегралом по Г _е

определена во всех точках в к-рых существует определенная касательная, т. е. почти всюду на Г. В теории и. т. К.-С. важное значение имеет основная лемма Привалова: предельный переход

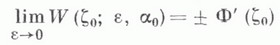
осуществляется для всех точек 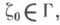кроме, быть может, точек множества меры нуль на Г, не зависящего от а ₀, равномерно относительно а ₀, в любом угле < 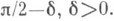Если сингулярный интеграл существует почти всюду на Г, то и. т. К.-С. имеет почти всюду на Г угловые граничные значения 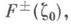для к-рых справедливы формулы Сохоцкого:

Верно и обратное: если и. т. К.-С. почти всюду на Г имеет угловые граничные значения изнутри и извне Г, то сингулярный интеграл существует и формулы (10) справедливы почти всюду на Г. Полного решения проблемы необходимых и достаточных условий существования граничных значений в достаточно простых терминах для и. т. К.-С. и даже для и. т. К.-Л. пока (1982) не получено.

В отличие от рассмотренного выше случая и. т. <К. по гладкой кривой Г, даже при наличии угловых граничных значений, и. т. К.-С. уже, вообще говоря, не является непрерывной функцией в окрестности точки слева или справа от Г. Здесь известно, напр., что и. т. К.-Л. (9) непрерывен в замкнутой области , ограниченной спрямляемым контуром Г, при дополнительном условии, что его плотность 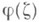удовлетворяет на Г условию Липшица

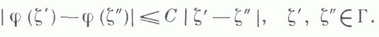
Относительно и. т. К.-Л. (9) говорят, что он обращается в К. и.

понимаемый в смысле Лебега, если угловые граничные значения 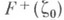изнутри Г совпадают с 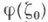почти всюду на контуре Г. Иначе говоря, интеграл (9) обращается в К. и. (11), если угловые граничные значения извне Г равны нулю почти всюду на Г. Относящаяся сюда теорема Голубева - Привалова гласит; суммируемая функция 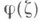на Г тогда и только тогда представляет собой угловые граничные значения нек-рого К. и. изнутри Г, когда равны нулю все моменты

Если выполнены аналогичные (12) условия

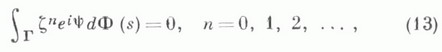
то и. т. К.-С. (8) обращается в интеграл Коши-Стилтьеса (и. К.-С.):

т. е. угловые граничные значения изнутри Г совпадают с производной почти всюду на Г или, иначе говоря, угловые граничные значения извне Г равны нулю почти всюду на Г. Условия (13) сразу обеспечивают абсолютную непрерывность функции Ф(s) на отрезке [0, l], а следовательно, на самом деле в этом случае и. К.-С. (14) является интегралом К о ш и - Лебега (и. К.-Л.) с плотностью . Таким образом, класс функций, представимых и. К.-С., совпадает с классом функций, представимых и. К.-Л.

Важной задачей представляется внутренняя харак-теризация классов функций, регулярных в области D, ограниченной замкнутой спрямляемой кривой Г, и представимых К. и. (11), и. т. К.-Л. (9) или и. т. К.-С. (8) (о наиболее важных классах 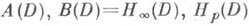и N*(D).см. в ст. Граничные свойства аналитических функций).

В простейшем случае, когда } - единичный круг и - единичная окружность, и. т. К.-С., принимающий в этом случае вид

изображает всегда функцию класса Обратная теорема неверна: совокупность функций классов шире, чем совокупность функций, представимых в виде (15). Напротив, совокупность функций, представимых в Dи. К.-С. или К. и., совпадает с классом Н ₁.

В случае произвольной односвязной области D, ограниченной спрямляемой кривой Г, класс функций, представимых в D и. К.-С. или К. и., совпадает с классом Смирнова Ej (см. Граничные свойства аналитических функций). Характеристики классов функций, пред-ставимых и. т. К.-С. или и. т. К.-Л., значительно сложнее.

Пусть f(z) - произвольная (не аналитическая) функция класса С ¹ в конечной замкнутой области 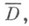ограниченной кусочно гладкой жордановой кривой L. Иногда интегральной формулой Коши наз. также следующее обобщение классич. формулы (1):

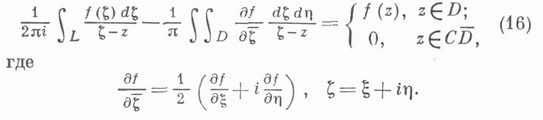
Эта формула встречается, начиная, по-видимому, с работ Д. Помпею (D. Pompeiu, 1912). Она известна также как формула Помпею, формула Бореля-Помпею, формула Коши- Грина и находит многочисленные приложения в теории обобщенных аналитич. функций, сингулярных интегральных уравнений и в различных прикладных вопросах.

Пусть f(z) - регулярная аналитич. функция многих комплексных переменных в замкнутом поликруге 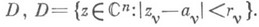Тогда в каждой точке Dфункция f(z) представима кратным интегралом Коши:

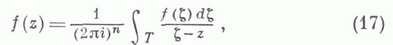
где

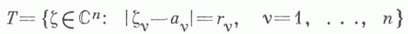
- остов поликруга,

Формула (17) дает простейший

аналог К. и. для окружности 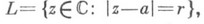но при n>1 интегрирование в (17) распространено уже не на всю границу поликруга, а лишь на его остов. Вообще, пусть 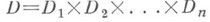- поликруговая область в СЩ, составленная как произведение односвязных плоских областей Dс гладкими границами

- остов D, представляющий собой гладкое и-мерное многообразие. Формула (17) распространяется и на этот случай.

Большое значение в теории аналитич. функций многих комплексных переменных имеют более глубокие обобщения интегральной формулы Коши, в первую очередь такие, как Лере формула, названная самим Ж. Лере (J. Leray) формулой Коши - Фантапье, и Вохнера - Мартинелли представление. В связи с этим при n>1 изучаются в основном граничные свойства интегральных представлений, отличных от (17).

Лит.:[1] С а u с h у A. L., Sur la mecanique celeste et sur un nouveau calcul appele calcul des limites, Turin, 1831 (или Euvres completes, ser. 1, t. 8, P., 1892); [2] Ш а б а т Б. В., Введение в комплексный анализ, 2 изд., ч. 1-2, 1976; [3] М а р-кушевич А. И., Теория аналитических функций, 2 изд., т. 1. М., 1967; [4] М у с х е л и ш в и л и Н. И., Сингулярные интегральные уравнения, 3 изд., М., 1968; [5] Владимиров В. С., Методы теории функций многих комплексных переменных, М., 1964; [6] П р и в а л о в И. И., Интеграл Cauchy, Саратов, 1918; [7] е г о же, Граничные свойства аналитических функций, 2 изд., М.- Л., 1950; [8] X а в и н c о н С. Я., в кн.: Итоги науки. Математический анализ. 1963, М., 1965, с. 5-80; [9] X в е д е л и д з е Б. В., в кн.: "Современные проблемы математики", т. 7, М., 1975, с. 5-162; [10] С а 1 d е r o n А. Р., "Proc. Nat. Acad. Sci. USA", 1977, v. 74, №4, p. 1324-27. Е. Д. Соломенцев.