КАРДИНАЛЬНОЕ ЧИСЛО

трансфинитное число, мощность по Кантору, кардинал множества A,- такое свойство этого множества, к-рое присуще любому множеству В, равномощному А. При этом два множества Аи Вназ. равномощными, если существует взаимно однозначная функция f :с областью определения Аи множеством значений В. Г. Кантор (G. Cantor) определял К. ч. множества Акак такое его свойство, к-рое остается после абстрагирования от качества элементов множества Аи от их порядка. Чтобы подчеркнуть этот двойной акт абстрагирования, Г. Кантор для обозначения К. ч. множества Аввел символ Из других обозначений К. ч. множества Анаиболее употребительны символы card Аи | А|. Если А- конечное множество, содержащее пэлементов, то card A = n. Если Z⁺- множество всех натуральных чисел, то card Z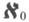⁺ = (см. Алефы). Если R - множество всех действительных чисел, то card R = с - мощность континуума. Множество 2 ^А всех подмножеств множества Ане равномощно ни самому А, ни его подмножеству (теорема Кантора). В частности, никакие два из множеств

не равномощны. При А= Z⁺ получается бесконечно много различных бесконечных К. ч. Другие К. ч. получаются, если взять объединение Qмножеств, входящих в (1), и построить последовательность, аналогичную (1), положив A = Q. Этот процесс можно продолжать бесконечно. Шкала всех бесконечных К. ч. намного богаче шкалы конечных мощностей. Более того, их так много, что нельзя образовать множества, содержащего по крайней мере по одному К. ч.

Для К. ч. определяются операции сложения, умножения, возведения в степень, а также взятие логарифма и извлечение корня. Так, К. ч. d=a+b наз. суммой К. ч. a и b, если каждое множество мощности d можно представить в виде объединения двух непересекающихся множеств Аи В мощностей а и 3 соответственно; К. ч. g=ab наз. произведением К. ч. a и b, если уявляется К. ч. декартова произведения А В, причем card A=a и card B=b. Сложение и умножение К. ч. коммутативно и ассоциативно, а умножение дистрибутивно относительно сложения. К. ч. х=a^b наз. степенью с основанием а и показателем b, если каждое множество мощности у. равномощно множеству А ^B, где card А=a. и card B=b. К. ч. a. не больше К. ч. b, a<b, если каждое множество мощности а равномощно нек-рому подмножеству множества мощности b. Если и то а= Р(теорема Кантора-Бернштейна ), так что шкала К. ч. линейно упорядочена. Более того, для каждого К. ч. b множество {a : a<b} вполне упорядочено, что позволяет определить логарифм log_ab К. ч. b по основанию К. ч. a, как наименьшее К. ч. утакое, что и корень a-й степени из К. ч. Р,как наименьшее К. ч. d такое, что

Любое К. ч. aможно отождествить с наименьшим порядковым числом мощности a. В частности, 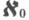соответствует порядковому числу w₀, 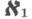- порядковому числу w₁, и т. д. Таким образом, шкала К. ч. является тюдшкалой шкалы порядковых чисел. Ряд свойств порядковых чисел переносится на К. ч., однако эти же свойства можно определить и "внутренним" способом. Если a_t<b_t для каждого и card то

(теорема Кёнига). Если в (2) положить T=Z⁺ и 1<a_n<a_n+1, то

В частности, ни для какого К. ч.степень нельзя представить в виде суммы членов бесконечно возрастающей последовательности меньших К. ч. Для каждого К. ч. а определяется К. ч. сf(a) - конфинальный характера, как наименьшее К. ч. утакое, что если b_t<a для всех и card T=y. Если сf(a)=a, то а наз. регулярным. К. ч., не являющееся регулярным, наз. сингулярным. Для любого К. ч. анаименьшее К. ч. а ⁺ , следующее за ос, является регулярным. Примером сингулярного К. ч. является К. ч. аш, из левой части формулы (3) при условии, что ш _о<а ₁. В этом случае

сf(a_w0)=w₀<a_w0.

К ч. а наз. предельным, если для любого К. ч. р<а существует К. ч. утакое, что b<g<a. Примеры предельных К. ч.: w₀ и a_w0. Непредельным К. ч. является w₁. Регулярное и предельное К. ч. называется слабо недостижимым. К. ч. a называется доминантным, если для любого b<a выполняется 2^b <a. Доминантное и регулярное К. ч. наз. сильно недостижимым. Из обобщенной континуум-гипотезы вытекает, что класс сильно недостижимых К. ч. совпадает с классом слабо недостижимых К. ч. Классы недостижимых К. ч. допускают дальнейшую классификацию (так наз. схема Мало), к-рая приводит к определению гипернедостижимых К. ч. Существование сильно (слабо) недостижимых К. ч., больших w₀, оказывается независимым от обычных аксиом как аксиоматической, так и наивной теории множеств.

К. ч. aназ. измеримым (точнее, {0, 1}-измеримым), если существует множество Амощности aи функция m, определенная на всех элементах семейства 2 ^А, принимающая значения 0 или 1 и такая, что m(A)=1, h{a}= 0 для любого аОАи если {Х _п: nОw₀} - последовательность, состоящая из попарно непересекающихся подмножеств А, то

Каждое К. ч., меньшее первого несчетного сильно недостижимого К. ч., неизмеримо (теорема Улама), так что первое измеримое К. ч. непременно сильно недостижимо. Однако первое измеримое К. ч. значительно больше, чем первое несчетное сильно недостижимое К. ч. (теорема Тарского). Неизвестно (1978), противоречит ли аксиомам теории множеств гипотеза о существовании измеримых К. ч.

Лит.:[1] Александров П. С, Введение в теорию множеств и общую топологию, М., 1977; [2] Кантор Г. в кн.: Новые идеи в математике, сб. 6, СПБ, 1914, с. 90-184; [3] Xаусдорф Ф., Теория множеств, пер. с нем., М.- Л., 1937; [4] Куратовский К., Мостов г, кий А., Теория множеств, пер. с англ., М., 1970; [5] Siеrрirtsk i W. Cardinal and ordinal numbers, Warsz., 1958 (2 wyd. 1965).

Б. А. Ефимов.