Признак Дини — Признак Дини признак поточечной сходимости ряда Фурье. Несмотря на то, что ряд Фурье функции из сходится к ней в смысле нормы, он вовсе не обязан сходиться к ней поточечно (даже в случае непрерывной функции). Тем не менее, при некоторых… … Википедия
Признак Лобачевского — признак сходимости числового ряда, предложенный Лобачевским между 1834 и 1836. Пусть есть убывающая последовательность положительных чисел, тогда ряд сходится или расходится одновременно с рядом … Википедия
Признак Дирихле — Признак Дирихле теорема, указывающая достаточные условия сходимости несобственных интегралов и суммируемости бесконечных рядов. Названа в честь немецкого математика Лежёна Дирихле. Содержание … Википедия
Признак Жордана — признак сходимости рядов Фурье: если периодическая функция имеет ограниченную вариацию на отрезке , то её ряд Фурье сходится в каждой точке к числу ; если при этом функция непрерывна на отрезке … Википедия
Признак Раабе — (признак Раабе Дюамеля) признак сходимости знакоположительных числовых рядов, установленный Йозефом Людвигом Раабе (Joseph Ludwig Raabe) и независимо Жан Мари Дюамелем. Содержание 1 Формулировка 2 Формул … Википедия
Признак Бертрана — признак сходимости числовых рядов с положительными членами, установленный Жозефом Бертраном. Содержание 1 Формулировка 2 Формулировка в предельной форме … Википедия
Признак Гаусса — общий признак сходимости числовых рядов с положительными членами, установленный в 1812 году Карлом Гауссом, при исследовании сходимости гипергеометрического ряда. Формулировка Пусть дан ряд и ограниченная числовая последовательность . Тогда если… … Википедия
Признак Ермакова — признак сходимости числовых рядов с положительными членами, установленный Василием Ермаковым. Его специфика заключается в том, что он превосходит все прочие признаки своей чувствительностью . Эта работа опубликована в статьях: «Общая теория… … Википедия
Признак Жамэ — признак сходимости числовых рядов с положительными членами, установленный Пьером Жамэ. Содержание 1 Формулировка 2 Формулировка в предельной форме … Википедия
Признак Куммера — общий признак сходимости числовых рядов с положительными членами, установленный Эрнстом Куммером. Содержание 1 Формулировка 2 Формулировка в предельной форме … Википедия

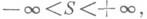 и каком-либо d>0, то ряд Фурье функции f(x)в точке х 0 сходится к числу S. Д. п. доказан У. Дини [1]. Его утверждение окончательно в следующем смысле. Если
и каком-либо d>0, то ряд Фурье функции f(x)в точке х 0 сходится к числу S. Д. п. доказан У. Дини [1]. Его утверждение окончательно в следующем смысле. Если  - такая непрерывная функция, что функция m(t)/t не интегрируема в окрестности точки 2=0, то можно найти непрерывную функцию f(t), ряд Фурье к-рой расходится в точке t=0, причем
- такая непрерывная функция, что функция m(t)/t не интегрируема в окрестности точки 2=0, то можно найти непрерывную функцию f(t), ряд Фурье к-рой расходится в точке t=0, причем