КЭЛЕРОВО МНОГООБРАЗИЕ — комплексное многообразие, на к ром можно ввести Кэлера метрику. Иногда такие многообразия на … Математическая энциклопедия
ОДНОРОДНОЕ КОМПЛЕКСНОЕ МНОГООБРАЗИЕ — комплексное многообразие М, группа автоморфизмов к рого транзитивно действует на М. Все односвязные одномерные комплексные многообразия сфера Римана, комплексная плоскость и верхняя комплексная полуплоскость однородны. Многообразие G/H смежных… … Математическая энциклопедия
ХОДЖА МНОГООБРАЗИЕ — комплексное многообразие, на к ром можно задать метрику Ходжа, т. е. Кэлера метрику, фундаментальная форма к рой определяет целочисленный класс когомологий. Компактное комплексное многообразие является X. м. тогда и только тогда, когда оно… … Математическая энциклопедия
АЛГЕБРАИЧЕСКОЕ МНОГООБРАЗИЕ — один из основных объектов изучения алгебраич. геометрии. Современное определение А. м. над полем kкак приведенной схемы конечного типа над полем kпретерпело длительную эволюцию. Классич. определение А. м. ограничивалось аффинными и проективными… … Математическая энциклопедия
ТОРЕЛЛИ ТЕОРЕМА — обобщения теорема, утверждающая, что структура Ходжа (матрица периодов) в когомологиях алгебраического или кэлерова многообразия Х полностью характеризует поляризованное многообразие X. Классич. Т. т. относится к случаю кривых (см. [1], [2]) и… … Математическая энциклопедия
ЛЕФШЕЦА ТЕОРЕМА — 1) Л. т. о неподвижных точках, Лефшеца Хопфа теорема, теорема, позволяющая выразить число неподвижных точек непрерывного отображения через его Лефшеца число. Так, если непрерывное отображение f: конечного клеточного пространства Xне имеет… … Математическая энциклопедия
ГАРМОНИЧЕСКАЯ ФОРМА — внешняя дифференциальная форма на римановом многообразии М, удовлетворяющая уравнению , где Лапласа оператор, соответствующий римановой метрике на М, а оператор, сопряженный к внешнему дифференциалу d. Если имеет компактный носитель, то… … Математическая энциклопедия
ЛАПЛАСА ОПЕРАТОР — лапласиан, дифференциальный оператор определяемый формулой (здесь координаты в ), а также некоторые его обобщения. Л. о. (1) является простейшим эллиптич. дифференциальным оператором 2 го порядка. Л. о. играет важную роль в математич. анализе,… … Математическая энциклопедия
СИГМА-МОДЕЛИ — ( модели) модели теории поля, в к рых т скалярных полей (i=1, ..., т )могут рассматриваться как задающие отображение d мерного пространства времени (произвольной сигнатуры) в нек рое многообразие М размерности тс метрикой … Физическая энциклопедия
СИМПЛЕКТИЧЕСКАЯ СТРУКТУРА — замкнутая невырожденная дифференциальнаяформа степени 2. Многообразие, снабжённое С. с., наз. симплектическиммногообразием. В каждом касательном пространстве С. с. задаёт кососкалярноепроизведение (см. в ст. Симплектическая группа). Кососкалярное … Физическая энциклопедия
 на пространстве
на пространстве 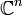 .
. .
.