ГАРМОНИЧЕСКАЯ ФОРМА

внешняя дифференциальная форма на римановом многообразии М, удовлетворяющая уравнению , где Лапласа оператор, соответствующий римановой метрике на М, а 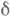- оператор, сопряженный к внешнему дифференциалу d. Если 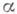имеет компактный носитель, то гармоничность формы равносильна равенствам 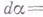Г. ф. степени рна Мобразуют векторное пространство 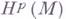над полем 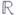. Если рнманово многообразие Мкомпактно, то 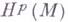конечномерно, как ядро эллиптич. оператора . Поскольку Г. ф. замкнута, в силу теоремы де Рама возникает естественное отображение пространства 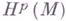в пространство 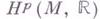вещественных когомологий степени рмногообразия М. Из Ходжа теоремы, следует, что это отображение является изоморфизмом. В частности, гармонич. функции, то есть Г. ф. степени 0, на связном компактном многообразии постоянны.

Г. ф. на компактном римановом многообразии инвариантны относительно любой связной группы изомет-рий этого многообразия, а для симметрического пространства Мпространство 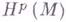совпадает с пространством р-форм, инвариантных относительно наибольшей связной группы изометрий.

Параллельная теория Г. ф. существует для эрмитовых многообразий М. Г. ф. на эрмитовом многообразии М - это комплексная форма, лежащая в ядре оператора Бельтрами - Лапласа . Г. ф. типа 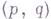составляют пространство над . Если Мкомпактно, то конечномерно и естественно изоморфно пространству когомологий Дольбо. В случае, когда М- кэлерово многообразие, эти два понятия Г. ф. фактически совпадают, поскольку В этом случае

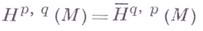
и

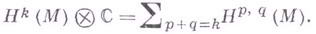
Пусть - кэлерова форма на М, L - оператор внешнего умножения на - сопряженный к Lоператор, 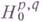(М) - пространство примитивных гармонических форм типа , т. е. форм 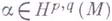, для которых 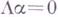. Для справедливо равенство

Для компактного кэлерова многообразия пространство совпадает с пространством голоморфных форм степени р. В частности,

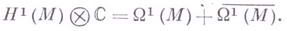
Изучение гармонич. функций и форм на римановых поверхностях восходит к Б. Риману (В. Riemann), сформулированные к-рым теоремы существования были полностью обоснованы к началу 20 в. Теория Г. ф. на компактных римановых многообразиях была впервые изложена У. Хеджем (см. [1]).

В дальнейшем были даны различные обобщения теории Г. <ф. Пусть на римановом (соответственно эрмитовом) многообразии Мзадано локально плоское (соответственно аналитическое) векторное расслоение Еи пусть на слоях расслоения Езадана евклидова (соответственно эрмитова) метрика. При помощи надлежащего обобщения оператора Лапласа (соответственно Бельтрами - Лапласа) (см. [4], [8]) определяются пространства 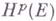(соответственно 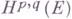) гармонич. форм со значениями в Е(см. Дифференциальная форма). Если Мкомпактно, то эти пространства конечномерны и изоморфны соответствующим пространствам когомологий де Рама и Дольбо, допускающим в свою очередь интерпретацию в терминах когомологий пучков.

В случае локально плоского расслоения эти когомологпи тесно связаны также с когомологиями группы Если Мне компактно, то пространство Г. ф. с интегрируемым квадратом изоморфно пространству кого-мологий комплекса форм с интегрируемым квадратом [2]. В случае, когда М- область с гладкой границей и компактным замыканием 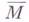в кэлеровом многообразии можно рассматривать также пространство Г. ф. типа со значениями в векторном аналитич. расслоении Енад гладких в Ми непрерывных в Если Мстрого псевдовыпукла, то это пространство конечномерно и изоморфно пространству когомологий Дольбо, соответствующему Енад М[9].

Г. ф. являются мощным средством изучения когомологий вещественных и комплексных многообразий, а также когомологий дискретных групп. Из теории Г. ф. выводятся основные когомологич. свойства компактных кэлеровых многообразий и, в частности, проективных алгебраич. многообразий [1], [4], [5]. С помощью Г. <ф. удается установить связь между кривизной компактного риманова многообразия и тривиальностью некоторых его групп когомологий [6], [7]. Аналогичные связи имеют место в комплексной анадитич. геометрии (см. [4]. [5]) и в теории дискретных групп преобразований (см. [8]).

Лит.:[1]Hodge W. V. D., The theory and applications of harmonic integrals, 2 ed., Camb., 1952; [2] де Рам Ж., Дифференцируемые многообразия, пер. с франц., М., 1956; [3] Шварц Л., Комплексные аналитические многообразия. Эллиптические уравнения с частными производными, пер. с исп., М., 1964; [4] Уэллс Р., Дифференциальное исчисление на комплексных многообразиях, пер. с англ., М., 1976; [5] Чжэнь Шан-шэнь, Комплексные многообразия, пер. с англ., М., 1961; [6] Goldberg S., Curvature and homology, N. Y.- L., 1962; [7] Яно К., Бохнер С., Кривизна и числа Бетти, пер. с англ., М., 1957; [8] Мацусима И., Мураками С., "Математика", 1965, 9 : 5, с. 27-77; [9] Кон Д ж. Д ж., "Математика", 1964, 8 : 1, с. 108-41; 8 : 3, с. 80-101.