- СИГМА-МОДЕЛИ
- СИГМА-МОДЕЛИ
-
(
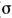 -модели)- модели теории поля, в к-рых т скалярных полей
-модели)- модели теории поля, в к-рых т скалярных полей 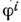 (i=1, ..., т )могут рассматриваться как задающие отображение
(i=1, ..., т )могут рассматриваться как задающие отображение 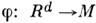 d-мерного пространства-времени
d-мерного пространства-времени 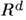 (произвольной сигнатуры) в нек-рое многообразие М размерности тс метрикой
(произвольной сигнатуры) в нек-рое многообразие М размерности тс метрикой 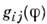 ,причём действие имеет вид:
,причём действие имеет вид: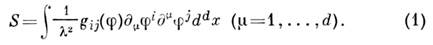
Здесь
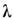 - безразмерная константа связи, х - точка d-мерного пространства-времени,
- безразмерная константа связи, х - точка d-мерного пространства-времени,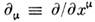 ,
,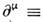
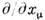 (по совпадающим верх. и ниж. индексам предполагается суммирование).
(по совпадающим верх. и ниж. индексам предполагается суммирование).Исторически первая С.-м. возникла как эфф. теория безмассовых возбужденийв следующей задаче. Рассмотрим теорию ( т+ 1)-компонентного поляи с действием
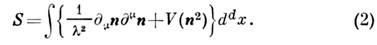
Если потенциал V(n2 )обладает минимумом при n2= 1, то вблизи минимума имеются одно массивное поле, описывающее флуктуациимодуля
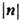 ,и т безмассовых полей, описывающих флуктуации направления поля ис сохранением величины n2 = 1. Безмассовые поля допускают интерпретациюкак координаты
,и т безмассовых полей, описывающих флуктуации направления поля ис сохранением величины n2 = 1. Безмассовые поля допускают интерпретациюкак координаты 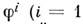 , ..., т )на сфере n2 = 1, и вклад полей
, ..., т )на сфере n2 = 1, и вклад полей 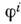 в действие (2) даётся ф-лой (1), где
в действие (2) даётся ф-лой (1), где 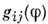 - индуциров. метрика на сфере. Первое приложение этой схемы было связанос теорией трёх псевдоскалярных
- индуциров. метрика на сфере. Первое приложение этой схемы было связанос теорией трёх псевдоскалярных 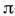 -мезонов, <к-рые отождествлялись с полями
-мезонов, <к-рые отождествлялись с полями 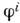 в случае m = 3, а роль массивного поля | п| играла т. н.
в случае m = 3, а роль массивного поля | п| играла т. н.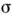 -частица, <к-рая и дала назв. модели. Дальнейшее развитие в этом направлении привелок Скирма модели, эффективно описывающей низкоэнергетич. предел квантовойхромодинамики (КХД) и физику адронов.
-частица, <к-рая и дала назв. модели. Дальнейшее развитие в этом направлении привелок Скирма модели, эффективно описывающей низкоэнергетич. предел квантовойхромодинамики (КХД) и физику адронов.С.-м. с действием (1) допускает два обобщения. Во-первых, вместо плоскогоd-мерного пространства-времени
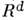 можно рассматривать искривлённое. При этом в (1) появится метрика (гравитац. <поле)
можно рассматривать искривлённое. При этом в (1) появится метрика (гравитац. <поле)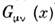 и действие приобретёт вид:
и действие приобретёт вид: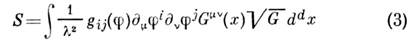
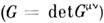 . Имеетсмысл также рассматривать пространство-время произвольной топологии. Такиетеории лучше всего изучены в случае d =2, они играют значит. рольв совр. теории струн (см. Струн теория). Для струнных приложенийпредставляют также интерес С.-м., в к-рых М не являются многообразиями, <а могут иметь разл. рода сингулярности, при этом действие должно быть доопределенов сингулярных точках. Во-вторых, при нек-рых значениях d (напр.,d=1, 2) можно рассматривать суперсимметричные (см. Суперсимметрия )С.-м.,в к-рых
. Имеетсмысл также рассматривать пространство-время произвольной топологии. Такиетеории лучше всего изучены в случае d =2, они играют значит. рольв совр. теории струн (см. Струн теория). Для струнных приложенийпредставляют также интерес С.-м., в к-рых М не являются многообразиями, <а могут иметь разл. рода сингулярности, при этом действие должно быть доопределенов сингулярных точках. Во-вторых, при нек-рых значениях d (напр.,d=1, 2) можно рассматривать суперсимметричные (см. Суперсимметрия )С.-м.,в к-рых 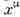 заменяются на координаты
заменяются на координаты 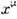 ,
,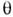 в суперпространстве (
в суперпространстве (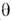 - нечётная координата), а поля
- нечётная координата), а поля 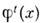 - на суперполя
- на суперполя 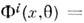 =
=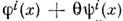 . Здесь
. Здесь 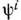 - фермионные компоненты суперполей, к-рые можно интерпретировать как касательныевекторы к многообразию М.
- фермионные компоненты суперполей, к-рые можно интерпретировать как касательныевекторы к многообразию М.Совр. интерес к С.-м. объясняется гл. обр. их прямой связью с геометрией. <Геом. структуры на многообразии М проявляются в физ. свойствах соответствующихС.-м. Напр., если М - однородное многообразие, М = G/H, тоС.-м. (1) может быть альтернативным образом описана как С.-м. на М =G, взаимодействующая с дополнит. калибровочным полем, отвечающимгруппе Н. Это одно из обстоятельств, связывающих С.-м. с теориями Янга- Миллса полей. Другие яркие примеры проявления геометрии . в структуре С.-м. связаны с суперсимметричными С.-м. В случае d= 2 С.-м. обладает расширенной (N = 2)-суперсимметрией, если многообразие . кэлерово, и (N= 4)-суперсимметрией, если М гиперкэлерово(см. Симплектическое многообразие). В случае d =4 суперсимметричныеС.-м. существуют только на кэлеровых многообразиях, а для (N =2)-суперсимметриитребуется гиперкэлерово многообразие. Несколько иные ограничения на геометрию . возникают, если строить суперсимметричную С.-м., взаимодействующуюс супергравитацией[т. е. суперобобщение действия (3)].
С.-м. являются удобным инструментом исследования общих свойств квантовойтеории поля (КТП). Уже при d =1 С.-м. позволяют исследовать проблемуупорядочения операторов. В случае однородных многообразий или суперсимметричныхС.-м. <ставится и исследуется вопрос о совместимости разл. способов упорядочениясо свойствами симметрии теории. Мн. С.-м. при d =2 оказываютсяочень похожими по своим свойствам на 4-мерные теории Янга - Миллса. В частности, <имеются асимптотическая свобода и широкий спектр непертурбативныхявлений, включая спонтанное нарушение симметрии и её восстановление, <инстантонные флуктуации (см. Инстантон), образование конденсатов(в т. ч. фермионных пар в суперсимметричных С.-м.). Это позволяет оцениватьприменимость разл. непертурбативных методов, первоначально развитых дляизучения явления конфайнмента в КХД (инстантонное исчисление, решёточныеи компьютерные вычисления и др.), на другом, значительно более простомпримере двумерной теории.
Выше отмечалось, что С.-м. обычно возникают как эфф. теории безмассовыхполей в более общих нелинейных теориях поля. В важных приложениях эти степенисвободы отвечают коллективным возбуждениям и не входят в число первичныхполей исходной теории. Чаще всего в С.-м. поля описывают квазичастицы, <возникающие при спаривании фермионов. По существу таковы упоминавшиесяя-мезоны (составленные из кварка и антикварка, окружённых глюонным облаком).Др. важные примеры имеются в физике твёрдого тела ( квантовый Холла эффект, модели сверхпроводимости и др.) и в теории элементарных частиц (супергравитацияи др.).
С.-м., описывающие квазичастицы, чаще всего отличаются от моделей сдействием (1) - (3) добавлением аномальных слагаемых, связанных с нетривиальностьюгомотопич. групп
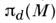 и
и 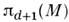 (см. Топология). В первом случае такие слагаемые в действии наз. т о п о л о г и ч ес к и м и, во втором - весс-зуминовскими членами (J. Wess, В. Zumino, 1973).Первые изменяют непертурбативные свойства теории, вторые - проявляютсяи в теории возмущений. Важный пример топологического заряда при d= 2 возникает уже в С.-м. на двумерной сфере, М =S2,заданной условием п 2 =1:
(см. Топология). В первом случае такие слагаемые в действии наз. т о п о л о г и ч ес к и м и, во втором - весс-зуминовскими членами (J. Wess, В. Zumino, 1973).Первые изменяют непертурбативные свойства теории, вторые - проявляютсяи в теории возмущений. Важный пример топологического заряда при d= 2 возникает уже в С.-м. на двумерной сфере, М =S2,заданной условием п 2 =1:
(
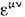 - антисимметрич. <тензор,
- антисимметрич. <тензор,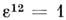 ). Выражение под интегралом (с учётом условия n2 = 1) являетсяполной производной,
). Выражение под интегралом (с учётом условия n2 = 1) являетсяполной производной,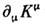 (нек-рого тока
(нек-рого тока 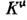 ),и интеграл
),и интеграл 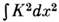 определяет весс-зуминовский член в одномерной (d= 1) С.-м. на М = S2. Весс-зуминовскийчлен при d =2 отвечает нетривиальной гомотопич. группе
определяет весс-зуминовский член в одномерной (d= 1) С.-м. на М = S2. Весс-зуминовскийчлен при d =2 отвечает нетривиальной гомотопич. группе 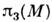 : в случае М= S2 он связан с топологич. характеристикойотображения трёхмерной сферы в двумерную (известной в математике как инвариантХопфа), а в случае М = S3 - с топологическим зарядом, <аналогичным (4).
: в случае М= S2 он связан с топологич. характеристикойотображения трёхмерной сферы в двумерную (известной в математике как инвариантХопфа), а в случае М = S3 - с топологическим зарядом, <аналогичным (4).При d =2 С.-м. является перенормируемой КТП, несмотря на сильнуюнелинейность действия. При этом в зависимости от выбора многообразия . С.-м. <в рамках теории возмущений может быть асимптотически свободной или иметьренормализац. поведение, отвечающее нуль-зарядной ситуации (см. Нуль-заряд). Двумерная С.-м. имеет тождественно нулевую бета-функцию, еслиона обладает (N = 4)-суперсимметрией. Этого же можно добиться введениемвесс-зуминовского или топологического члена с подходящим коэф. без обращенияк супереимметрии и гиперкэлерову многообразию.
Весс-зуминовские члены и топологич. заряды возникают в эффективных С.-м. <как отражение аномалий исходных фермионных теорий. Важную роль вС.-м. играют также их собственные квантовые аномалии. Аномальными могутбыть d-мерная общекоординатная инвариантность в теории с действием (3),калибровочная H -симметрия в случае М = G/H, вейлевская симметрия
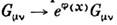 [где
[где 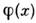 - нек-рое вещественное поле], имеющаяся в теории с действием (3) при .=2.
- нек-рое вещественное поле], имеющаяся в теории с действием (3) при .=2.Двумерные С.-м. с нулевой бета-функцией, являющиеся конформно-инвариантными(см. Конформная инвариантность), играют большую роль в теории струн, <где они описывают всевозможные решения струнных ур-ний движения. В настоящеевремя активно изучается вопрос о классификации всех конформно-инвариантныхтеорий и развиваются общие методы вычислений в конформных С.-м. Наиб. существ. <продвижение в этом направлении достигнуто пока для более узкого класса(N=2)-суперконформных моделей при d = 2, классификация к-рыхблизка к классификации особенностей в катастроф теории.
Лучше всего изучены одномерные С.-м. На совр. этапе исследований осн. <внимание уделяется развитию теории двумерных С.-м., как из-за их относит. <простоты, так и из-за явной связи с теорией Янга - Миллса и теорией струн. <Общая матем. теория таких С.-м. должна включать в себя теорию бесконечномерныхи квантовых Ли алгебр, но она ещё не разработана. Единый подходк изучению многомерных (<
2) С.-м. пока отсутствует. Лит.: Gell-Mann M., Levy M., The axial vector current in b-decay, «NUOVOCim.», 1960, v. 16, p. 705; W i t t e n E., Supersymmetry and Morse theory,«J. Dili. Geom.», 1982, v. 17, p. 661; Perelomov A., Chiral models: geometricalaspects, «Phys. Repts», 1987, v. 146, p. 136. А. Ю. Морозов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
