- Модулярная группа
-
Модулярная группа — группа
 всех преобразований Мёбиуса вида
всех преобразований Мёбиуса видагде
 — целые числа, причём
— целые числа, причём  .
.Модулярная группа отождествляется с факторгруппой
 . Здесь
. Здесь  — группа матриц
— группа матрицгде
 — целые числа,
— целые числа,  .
.Модулярная группа является дискретной группой преобразований верхней комплексной полуплоскости
 (плоскости Лобачевского) и допускает представление образующими
(плоскости Лобачевского) и допускает представление образующимии соотношениями
 , то есть является свободным произведением циклической группы порядка 2, порождённой
, то есть является свободным произведением циклической группы порядка 2, порождённой  , и циклической группы порядка 3, порождённой
, и циклической группы порядка 3, порождённой  .
.Для произвольного преобразования
 из модулярной группы справедливо равенство:
из модулярной группы справедливо равенство:Поскольку мнимая часть
 ненулевая, а числа
ненулевая, а числа  и
и  — целые, не равные нулю одновременно, то величина
— целые, не равные нулю одновременно, то величина  отделена от нуля (не может быть сколь угодно малой). Это означает, что в орбите любой точки есть такая, на которой мнимая часть достигает своего максимума.
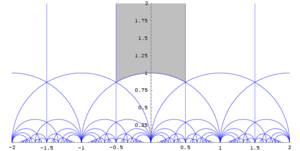
отделена от нуля (не может быть сколь угодно малой). Это означает, что в орбите любой точки есть такая, на которой мнимая часть достигает своего максимума.Фундаментальная область (каноническая) модулярной группы — это замкнутая область
Легко проверить, используя (1), что преобразования модулярной группы не увеличивают мнимую часть точек из
 . Из этого следует, что для того, чтобы две точки
. Из этого следует, что для того, чтобы две точки  принадлежали
принадлежали  , их мнимая часть должна быть одинакова:
, их мнимая часть должна быть одинакова:  . Таким условиям отвечают следующие преобразования и точки:
. Таким условиям отвечают следующие преобразования и точки: — любая точка;
— любая точка;


В частности, все точки области
 имеют тривиальный стабилизатор, кроме трёх:
имеют тривиальный стабилизатор, кроме трёх:Кроме того, из этого следует что при факторизации верхней полуплоскости по действию модулярной группы внутренние точки
 отображаются инъективно, тогда как граничные — склеиваются с точками, «зеркальными» к ним относительно прямой
отображаются инъективно, тогда как граничные — склеиваются с точками, «зеркальными» к ним относительно прямой  .
.Чтобы показать, что всякая точка из
 конгруэтна некоторой точке из
конгруэтна некоторой точке из  , рассмотрим в её орбите, порождённой преобразованиями
, рассмотрим в её орбите, порождённой преобразованиями  и
и  , точку с максимальной мнимой частью и с помощью целочисленного сдвига сдвинем так, чтобы вещественная часть её образа стала по модулю не больше, чем 1/2. Тогда образ принадлежит
, точку с максимальной мнимой частью и с помощью целочисленного сдвига сдвинем так, чтобы вещественная часть её образа стала по модулю не больше, чем 1/2. Тогда образ принадлежит  (иначе, если бы его модуль был меньше 1, с помощью преобразования
(иначе, если бы его модуль был меньше 1, с помощью преобразования  можно было бы строго увеличить мнимую часть).
можно было бы строго увеличить мнимую часть).Легко показать также, что преобразования
 и
и  порождают всю модулярную группу. Пусть
порождают всю модулярную группу. Пусть  — произвольное модулярное преобразование и
— произвольное модулярное преобразование и  — внутренняя точка
— внутренняя точка  . Как описано выше, найдём преобразование
. Как описано выше, найдём преобразование  переводящее
переводящее  в область
в область  . Точки
. Точки  и
и  лежат в
лежат в  , причём
, причём  — внутренняя, следовательно,
— внутренняя, следовательно,  . Тогда преобразование
. Тогда преобразование  лежит в стабилизаторе точки
лежит в стабилизаторе точки  , который тривиален. Следовательно,
, который тривиален. Следовательно,  лежит в группе, порождённой преобразованиями
лежит в группе, порождённой преобразованиями  и
и  .
.Интерес к модулярной группе связан с изучением модулярных функций, римановой поверхностью которых является факторпространство
 , отождествляемое с фундаментальной областью
, отождествляемое с фундаментальной областью  модулярной группы. Фундаментальная область
модулярной группы. Фундаментальная область  имеет конечную площадь, то есть модулярная группа есть фуксова группа первого рода.Категории:
имеет конечную площадь, то есть модулярная группа есть фуксова группа первого рода.Категории:- Аналитическая теория чисел
- Теория групп
- Комплексный анализ
Wikimedia Foundation. 2010.