МОДУЛЯРНАЯ ФУНКЦИЯ

эллиптическая модулярная функция, одного комплексного переменного - автоморфная функция комплексного переменного 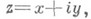ассоциированная с группой Г всех дробно-линейных преобразований 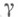вида

где 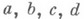- целые действительные числа (эта группа наз. модулярной). Преобразования группы Г переводят действительную ось в себя, и областью определения М. ф. можно считать верхнюю полуплоскость 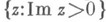Группа Г порождается двумя образующими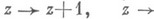 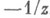. Фундаментальная область G модулярной группы изображена на рис. 1;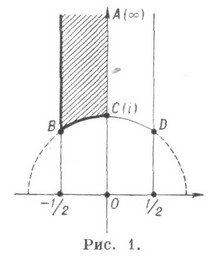

это - криволинейный четырехугольник ABCDА с вершинами , , 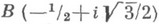, 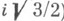две стороны к-рого А В и D А- отрезки прямых со ответственно 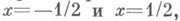a BD- дуга окружности . Участки границы АВ и ВС включаются в G,a CD и DA не включаются. Образы области Gпри всевозможных отображениях группы Г покрывают всю полуплоскость без пересечений.

Изучение М. ф. началось в 19 в. в связи с изучением эллиптич. функций и предшествовало появлению общей теории автоморфных функций. В теории М. ф. в качестве основных модулярных форм используются следующие тета-ряды:

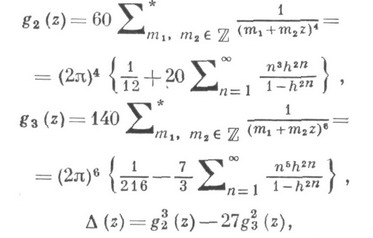
где , а звездочка означает, что нулевая пара ( т ₁ , т ₂ )=(0, 0) отбрасывается. Согласно терминологии К. Вейерштрасса (К. Weierstrass) это - относительные инварианты, играющие важную роль в его теории эллиптич. функций (см. Вейер штрасса эллиптические функции), а А наз. также дискриминантом. С точки зрения теории автоморфных функций это - автоморфные формы соответственно веса 2, 3 и 6, ассоциированные с модулярной группой. Основная М. ф. имеет вид

Функция J(z) наз. также абсолютным инвариантом. Она регулярна в верхней полуплоскости, а внутри фундаментальной области Gпринимает каждое конечное значение, кроме 0 и 1, в точности один раз; кроме того,

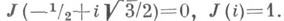
В теории эллиптич. функций М. ф. J(z) играет важную роль, позволяя по заданным вейерштрассовым относительным инвариантам 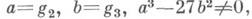определить периоды 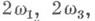а следовательно, и построить все эллиптич. функции Вейерштрасса. Если t - единственное в фундаментальной области решение уравнения 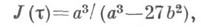то при 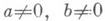имеем 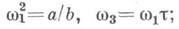при а=0 имеем 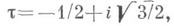и определяется из уравнения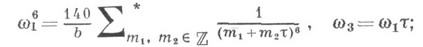

при b=0 имеем t=i, и w₁ определяется из уравнения

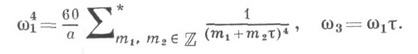
Для построения Якоби эллиптических функций удобнее, вместо J(z), функция

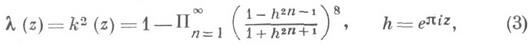
также называемая М. ф. На самом деле l(z). является автоморфной функцией только относительно подгруппы Г ₂ модулярной группы Г, причем к Г ₂ относятся все те преобразования вида (1), у к-рых (в качестве дополнительного условия) aи d- нечетные числа, bи с - четные. Фундаментальная область G₂ группы Г ₂ изображена на рис. 2;

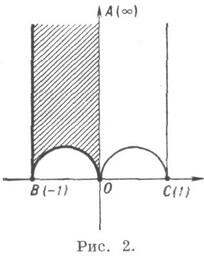
это - криволинейный четырехугольник ABOCA с вершинами A(оо), В(-1), 0, С(1),две стороны к-рого АВ и СА- отрезки прямых соответственно х=-1 и х=1, а ВО и ОС- дуги окружностей соответственно 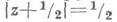и Участки границы слева от мнимой оси включаются в G₂, а ОС и СА не включаются. Функция l(z) также регулярна в верхней полуплоскости Im z>0. Внутри области G₂ она принимает каждое конечное значение, кроме 0 и 1, в точности один раз; кроме того,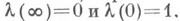 При заданном модуле эллиптич. функций Якоби кдля их построения необходима величина t=w₃ / w_1. или 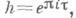к-рая однозначно определяется из уравнения . Практически, в нормальном случае 0<k<1 определяют сначала 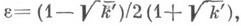где а затем строят решение этого уравнения в виде ряда 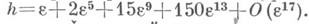М. ф.связаны формулой

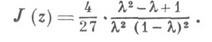
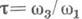М. ф.дает наиболее удобное представление конформных классов римановых поверхностей эллиптич. функций, когда род g =1. и эйлерова характеристика . Каждому значению wсоответствует решение уравнения , определяющее конформный класс и соответствующее поле эллиптич. функций. Напр., w=0соответствует параллелограмм периодов в виде ромба с углами 120° и 60°, а 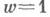- квадрат.

М. ф. применяются также при изучении конформных отображений, граничных свойств аналитических функций и предельных множеств. М. ф. дает конформное отображение левой половины фундаментальной области G(рис. 1), т. е. криволинейного треугольника ABCА, на верхнюю полуплоскость Im w>0, причем точки В, С, А переходят соответственно в 0, 1, . М. ф.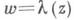отображает конформно криволинейный треугольник АВОА (рис. 2) на верхнюю полуплоскость, причем точки В, О, А переходят соответственно в

В геометрич. вопросах часто удобнее принять за область определения М. ф. единичный круг. При этом модулярная группа (1) переходит в модулярную группу автоморфизмов единичного круга. Напр., удобно применить дробно-линейное преобразование

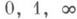переводящее верхнюю полуплоскость Im z>0 в единичный круг причем точки переходят соответственно в точки на единичной окружности (рис. 3). Тогда сложная функция есть М. ф., регулярная в единичном круге и принимающая в нем все значения, кроме 0, 1, оо. Она отображает конформно криволинейный треугольник ABCА (рис. 3)

на верхнюю полуплоскость Im z>0. Именно эта М. ф.используется при доказательстве Пикара теорем и в ряде других геометрических вопросов.

Лит.:[1] Гурвиц А., Курант Р., Теория функций, пер. [с нем.], М., 1968; [2] Ахиезер Н. И., Элементы теории эллиптических функций, 2 изд., М., 1970; [3] Форд Р., Автоморфные функции, пер. с англ., М.- Л., 1936; [4] Кlein F., Рriсke R., Vorlesungen uber die Theorie der elliptischen Modulfunktionen, Bd 1-2, Lpz., 1890-92. E. Д. Соломенцев.