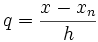Интерполяционный многочлен Ньютона
- Интерполяционный многочлен Ньютона
-
Интерполяционные формулы Ньютона — формулы вычислительной математики, применяющиеся для полиномиального интерполирования.
Если узлы интерполяции равноотстоящие и упорядочены по величине, так что xi + 1 − xi = h = const, то есть xi = x0 + ih, то интерполяционный многочлен можно записать в форме Ньютона.
Интерполяционные полиномы в форме Ньютона удобно использовать, если точка интерполирования находится вблизи начала (прямая формула Ньютона) или конца таблицы (обратная формула Ньютона).
Короткая форма интерполяционной формулы Ньютона
В случае равноудаленных центров интерполяции, находящихся на единичном расстоянии друг от друга, справедлива формула:
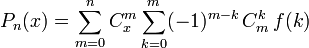
где 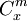 — обобщенные на область действительных чисел биномиальные коэффициенты.
— обобщенные на область действительных чисел биномиальные коэффициенты.
Прямая интерполяционная формула Ньютона
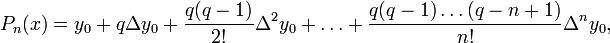 где
где 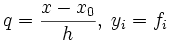 , а выражения вида Δkyi — конечные разности.
, а выражения вида Δkyi — конечные разности.
Обратная интерполяционная формула Ньютона
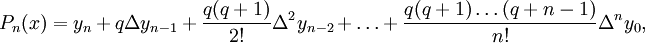 где
где 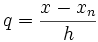
См. также
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Интерполяционный многочлен Ньютона" в других словарях:
Интерполяционный многочлен — Интерполяционный многочлен: Интерполяционный многочлен Лагранжа Интерполяционный многочлен Ньютона Интерполяция алгебраическими многочленами … Википедия
Интерполяционный многочлен Лагранжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для пар чисел , где все различны, существует единственный многочлен степени не более , для которого . В простейшем случае ( … Википедия
ИНТЕРПОЛЯЦИОННЫЙ ПРОЦЕСС — процесс получения последовательности интерполирующих функций {fn(z)} при неограниченном возрастании числа n условий интерполирования. Если интерполирующие функции fn(z)представлены в виде частных сумм некоторого функционального ряда, то последний … Математическая энциклопедия
Интерполяционные формулы Ньютона — Интерполяционные формулы Ньютона формулы вычислительной математики, применяющиеся для полиномиального интерполирования. Если узлы интерполяции равноотстоящие и упорядочены по величине, так что , то есть , то интерполяционный многочлен можно … Википедия
Интерполяционная формула Ньютона — Интерполяционные формулы Ньютона формулы вычислительной математики, применяющиеся для полиномиального интерполирования. Если узлы интерполяции равноотстоящие и упорядочены по величине, так что xi + 1 − xi = h = const, то есть xi = x0 + ih, то… … Википедия
Интреполирование по формулам Ньютона — Интерполяционные формулы Ньютона формулы вычислительной математики, применяющиеся для полиномиального интерполирования. Если узлы интерполяции равноотстоящие и упорядочены по величине, так что xi + 1 − xi = h = const, то есть xi = x0 + ih, то… … Википедия
Интерполирование с кратными узлами — Интерполирование с кратными узлами задача о построении многочлена минимальной степени, принимающего в некоторых точках (узлах интерполяции) заданные значения, а также заданные значения производных до некоторого порядка. Показывается, что… … Википедия
Интерполяция алгебраическими многочленами — функции f(x) на отрезке [a, b] построение многочлена Pn(x) степени меньшей или равной n, принимающего в узлах интерполяции x0, x1, ..., xn значения f(xi): Система уравнений, определяющих коэффициенты такого многочлена, имеет вид Её определителем… … Википедия
КОНЕЧНЫХ РАЗНОСТЕЙ ИСЧИСЛЕНИЕ — раздел математики, в к ром изучаются функции при дискретном изменении аргумента, в отличие от дифференциального и интегрального исчислений, где аргумент изменяется непрерывно. Пусть функция y=f(x)задана в точках xk=x0+kh(h постоянная, к целое).… … Математическая энциклопедия
Интерполяционные формулы — Интерполяционные формулы в математике формулы, дающие приближённое выражение функции при помощи интерполяции, то есть через интерполяционный многочлен степени , значения которого в заданных точках совпадают со значениями функции в этих… … Википедия
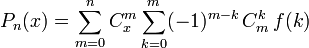
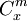 — обобщенные на область действительных чисел биномиальные коэффициенты.
— обобщенные на область действительных чисел биномиальные коэффициенты.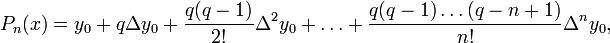 где
где 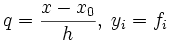 , а выражения вида Δkyi — конечные разности.
, а выражения вида Δkyi — конечные разности.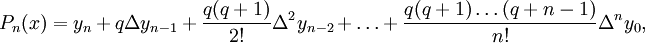 где
где