- Интреполирование по формулам Ньютона
-
Интерполяционные формулы Ньютона — формулы вычислительной математики, применяющиеся для полиномиального интерполирования.
Если узлы интерполяции равноотстоящие и упорядочены по величине, так что xi + 1 − xi = h = const, то есть xi = x0 + ih, то интерполяционный многочлен можно записать в форме Ньютона.
Интерполяционные полиномы в форме Ньютона удобно использовать, если точка интерполирования находится вблизи начала (прямая формула Ньютона) или конца таблицы (обратная формула Ньютона).
Содержание
Короткая форма интерполяционной формулы Ньютона
В случае равноудаленных центров интерполяции, находящихся на единичном расстоянии друг от друга, справедлива формула:
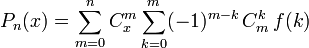
где
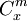 — обобщенные на область действительных чисел биномиальные коэффициенты.
— обобщенные на область действительных чисел биномиальные коэффициенты.Прямая интерполяционная формула Ньютона
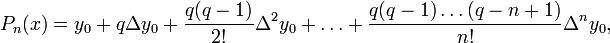 где
где 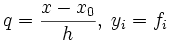 , а выражения вида Δkyi — конечные разности.
, а выражения вида Δkyi — конечные разности.Обратная интерполяционная формула Ньютона
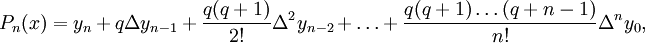 где
где 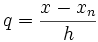
См. также
Wikimedia Foundation. 2010.
